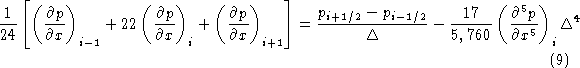
By requiring the minimum truncation error, the parameters 
were obtained such that (Figure 1b)
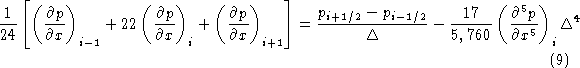
The tridiagonal system implied in (9) requires knowledge of the derivative of
p at both boundaries. By require the error on the fourth-order 
, we obtained the relations for the ''left'' boundary point,
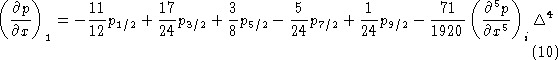
The ''right'' boundary point has the similar formulation.
The last terms in (2) and (9) suggest that the compact scheme can provide more
accuracy. The error ratio between the 4th-order compact and the 4th order
ordinary schemes is
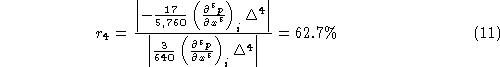
which means a more than 30% reduction of the truncation error when we use the
compact scheme.