Piecewise Approximation using Lower-Order Polynomials
Instructor Note: In this section, you’ll read about the concepts behind piecewise approximation using lower-order polynomials. Be sure you understand how we manage to match the number of unknown coefficients with the number of boundary conditions to be satisfied!
It is well known that the easiest way to connect two points is to use a first-order polynomial. The unknown coefficients of such a polynomial are found via satisfying two boundary conditions. Similarly, for N + 1 data points (nodes), i.e. N intervals, a piecewise linear approximation will have 2N unknown coefficients and, therefore, exactly 2N boundary conditions that can be used to find the unknown coefficients. Formally, given pairs (xi, yi), i = 1, 2, … , N + 1, such that x1 < x2 < …< xN+1, a piecewise linear interpolation for each interval xj ≤ x ≤ xj+1, i = 1, 2, …, N will be given by
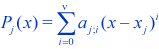
(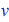 = 1) with two boundary conditions Pj(xj) = yj and Pj(xj+1) = yj+1. If we decide to use higher-order interpolating polynomials for each of N intervals (
= 1) with two boundary conditions Pj(xj) = yj and Pj(xj+1) = yj+1. If we decide to use higher-order interpolating polynomials for each of N intervals (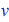 > 1), then the number of coefficients to be determined would certainly exceed the number of available boundary conditions, 2N. This would give us additional degrees of freedom, which, in turn, would insure a better appearance of our interpolation curve. For example, if we increase the order of the polynomials in the piecewise approximation up to two (
> 1), then the number of coefficients to be determined would certainly exceed the number of available boundary conditions, 2N. This would give us additional degrees of freedom, which, in turn, would insure a better appearance of our interpolation curve. For example, if we increase the order of the polynomials in the piecewise approximation up to two (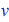 = 2), i.e. use the so-called "quadratic splines", we will be able to guarantee the continuity of the 1st-order derivative at all nodes.
= 2), i.e. use the so-called "quadratic splines", we will be able to guarantee the continuity of the 1st-order derivative at all nodes.
Instructor Note: Now review the different commonly used piecewise lower-order-polynomial approximations. Pay close attention to the choice of the order of these polynomials.
The table below shows the number of unknown coefficients for three different piecewise interpolations (through N + 1 points) compared to the number of readily available conditions.
| Linear ( 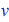 = 1) = 1) |
Quadratic ( 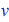 = 2) = 2) |
Cubic ( 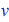 = 3) = 3) |
|
|---|---|---|---|
| Number of coefficients | 2N | 3N | 4N |
| Total Number of readily available conditions: | 2N | 3N – 1 | 4N – 2 |
| The numbers above are comprised of the numbers below. | |||
| Number of boundary conditions | 2N | 2N | 2N |
| Continuity of the 1st-order derivative | N – 1 | N – 1 | |
| Continuity of the 2nd-order derivative | N – 1 | ||
As you can see from this table, increasing the order of polynomials allows us to insure the continuity of the higher-order derivatives in the N – 1 intermediate points. This also results in a larger number of free parameters that can be used. For example, in the case of the cubic spline, which is comprised of N third-order interpolating polynomials, we end up having two free parameters (see the foremost right column in the table above). For example, we can use these parameters to vary the values of derivatives of the coordinates at the boundary points (initial and final slope). Let's consider these and some other conditions that might be used to make up for a deficiency in two equations and to be able to compute coefficients of the cubic spline.
Click on the 'Globally Determined Splines' button in the left navigation area to continue this discussion.
Back to top.
