Project Report: Using an Evolutionary Algorithm to Anticipate Military Technological Surprises

 

Neil Rowe and Eric Skalnes

U.S. Naval Postgraduate School

ncrowe@nps.edu

September, 2019

 

1.     Introduction

Technological surprise is an important concern of U.S. military organizations in a world in which the U.S. no longer has an advantage in many technologies (National Research Council, 2009).  Technological surprise can be a new weapon, something new demonstrated in conflict, something not identifiable as a weapon but influencing military operations, something not already familiar, or something that merely requires significant time for which to develop countermeasures (Handel, 1987).  Some technological developments can be anticipated like duplications of the capabilities of our own.  However, science and engineering can advance differently in other countries and lead to technological surprises that provide an asymmetric advantage to an adversary.  Technological surprises can be especially important for terrorists because small organizations can better conceal surprises.

Technological surprise relates to the useful distinction popularized by Donald Rumsfeld in a speech February 12, 2002 between “known unknowns” (things we know are possible but haven’t seen) and “unknown unknowns” (things we don’t know are possible and aren’t looking for).  Unknown unknowns are what can cause the most technological surprise.  While unknown unknowns are intended to be difficult to predict, there are some ways.  In the field of military technology, only a limited set of technological innovations provide military advantage.  Many possible unknown unknowns are too costly to implement, too ineffective in achieving military goals, or too redundant with existing technology.  We could search for the few unknown unknowns that could provide major advantages and prepare for them.

This paper will use the example of novelty in military vehicles (Beidel, 2012).  There are many other possible surprises (National Research Council, 2013), but this will serve as a starting point.  A classic example of technological surprise was “stealth” technology for military aircraft such as the U.S. B-2 bomber (Richardson, 2001).  This achieved a significantly reduced radar image due to novel carbon-fiber composite materials as well as using novel methods to conceal exhaust heat, making the aircraft very difficult to detect.  Another example is the use of a small boat to attack the USS Cole in October 2000 using technology of improvised explosive devices which had not previously been used against ships (U.S. Department of Defense, 2001). “Swarm” robotics, or groups of coordinated small vehicles such as drones, can also be surprising technology (Sahan and Spears, 2004).  Even though one small vehicle cannot do much, their working together can provide actions over a wider area than a single vehicle.

We wrote two programs to explore vehicle design using evolutionary algorithms.  Appendix A describes the first and preliminary version.  Appendix B reports work we did on the original topic of the research grant, the analysis of the applicability of the Libratus poker-playing AI program to military strategy.

2.     Formulating the finding of technological surprises as heuristic search

Finding technical surprises has been an important topic with many applications to design (Eberle, 1996; Adams, 2019; Petrov, 2019). Recent work has applied artificial-intelligence methods to this problem, mostly in the form of generating artistic behavior (Besold, Schorlemmen, and Smaill, 2015).   Finding interesting things is an instance of heuristic search, a concept with a long history in artificial intelligence.  Combinations of factors can be considered using a fitness function to find the best or near-best solution to a task.  Classic algorithms such as A* search can be used to solve heuristic-search problems efficiently without needing to consider every possible solution (or doing “exhaustive search”).

The problem of detecting technological surprises is a special kind of heuristic search in the space of possible surprising entities.  For our focus of military vehicles, heuristic search could consider possible vehicles that would provide surprises if encountered and thus cause difficulties for either defense or offense.  Finding surprises has been addressed with methods to enhance creativity such as “conceptual blockbusting” (Adams, 2015) which tries to systematically explore possibilities for the solution of a problem.  Particularly featured in blockbusting methods are factorization of search items into quasi-independent dimensions or properties that can be enumerated to find novel combinations.

Evolutionary algorithms for heuristic search can be particularly useful in exploring the space of all possible solutions by using random choices and ideas like “mutation” and “crossing” (Eiben and Smith, 2015).  To apply this to the finding of unknown unknowns, we need to formulate technological options as choices in a heuristic search.  We can do this by identifying properties of them and possible values of those properties.  We can consider random selections of those property values and rate them with a fitness function.  Then we can take the best options according to the fitness function and mutate them and combine (“cross”) them to evolve better technological surprises.

Evolutionary algorithms have been explored on occasion for conflict situations, as for weapons strike planning in (Rice et al, 2006) where the parameters to be optimized were weapons effectiveness, risk due to adversary actions, and lack of changes to the original plan.  They have also been explored for games such as for first-person shooter games in (Gravina and Loiacono, 2015) where the parameters were rate of fire, spread of trajectory, number of bullets shot at once, life span for bullets, speed, damage, damage radius, gravity effects, explosiveness of the hit, and maximum ammunition capable of being carried.  Two projects have explored the application of evolutionary algorithms specifically to military vehicles: (Tiao-Ping et al, 2010) designed naval platforms for a wargame, and (Fogel et al, 2006) built maximally effective aircraft for a World War I wargame.  In both these last two cases the goal was to optimize a set of vehicles rather than a single vehicle, a different one than the one we consider here.  It should be noted that all four of these projects focused on offensive capabilities, and it would be useful to investigate defensive capabilities as well.

3.     Demonstration implementation: Military vehicles

We wanted to discover new things, so it was essential to use unsupervised learning.  Appendix A describes our first approach, which used a different model of vehicles and different fitness function.

 

3.1. Properties

For military vehicles, we can identify the following properties:

·         Type of object, e.g. ship

·         Size

·         Ratio of length to width

·         Ratio of width to height

·         Overall shape

·         Number of occupants

·         Material of which it is made

·         Energy source (not often visible)

·         Propulsion method (not often visible)

·         Infrastructure needed to support propulsion (roads, rails, cables, or none)

·         Range of acceleration

·         Friction-reducing method, e.g. tires or streamlining

·         Speed range

·         Range of turning-rate

·         Habitat (land surface, water, air, space)

·         Frequency of occurrence

·         Count with which it occurs (as when it is used in swarms)

·         Visibility to optical systems

·         Visibility to radar

·         Owner (not often visible)

·         Purpose (not often visible)

·         Appearance (easy to change)

·         Color (easy to change)

·         Markings (easy to change)

·         Sounds generated (easy to change)

·         Signals generated (easy to change)

Some of these properties are numeric, so representative values on their ranges need to be identified in advance since the evolutionary algorithm will try to solve a combinatorial problem in choosing good values for properties.  We chose the following properties and possible values for a demonstration system:

·         Weight (numeric): 10, 50 250, 1250, 6250 kilograms

·         Volume (numeric): 1, 5, 25, 125 cubic meters

·         Power (numeric): 1, 10, 100, 1000 horsepower

·         Maneuverability interpreted as turn radius (numeric): 1, 2, 4, 8 meters

·         Count (numeric): 1 3, 10 items

·         Material (nonnumeric): wood, steel, plastic, composite

·         Habitat (nonnumeric): overland, water-surface, underwater, air, space

·         Shape (nonnumeric): car, ship, aircraft, box, sphere, plate

·         Appearance (nonnumeric): new, some usage, old

·         Color: gray, black, green, red

 

Thus the number of total possibilities (size of the search space) for our demonstration search for vehicles was thus .

 

3.2. An evolutionary algorithm

We have had good success on previous projects in exploring large search spaces when assigning 10 categories to property values.  Clearly this search space is too large for exhaustive search, since there are  combinations then on the above properties.  It is also too large for A* or other classic search algorithms because they reduce branching factors in the search tree but do not eliminate the need to try many combinations.  So evolutionary algorithms with stochastic (probabilistic) features look like the best hope here (De Jong, 2006).  Evolutionary algorithms can quickly find some decent possibilities, and then mutate and cross them to find better possibilities (Shah, Vargas-Hernandez, and Smith, 2003; Eiben and Smith, 2015).  “Mutate” would mean to change a few property values of a good candidate; “cross” would mean to mix property values of two good candidates.

The next section will describe our fitness function.  We also need to apply reasonableness criteria independent of the fitness function. An example would be a vehicle made of paper which by the physics of its material could not travel more than at a low speed.  Another example is an aircraft propelled by nuclear energy requiring such heavy shielding of the pilots that its weight made it cost-ineffective (Ruchl, 2019).  Reasonableness criteria need to be applied when generating possibilities so they can rule out unreasonable combinations as early as possible and save effort.

It should be emphasized that this evolutionary algorithm is just a tool for aiding planners.  It does not try to provide definitive advice to planners on what threats they should focus on, just suggest some things that they may not have thought about.  Thus the details of the planner are not fixed and should be modified in use to obtain results interesting to planners.

 

3.3. Modeling surprise for vehicles

A fitness function for an evolutionary algorithm needs to measure technological surprise or novelty.   Many approaches have been proposed to measure surprise or novelty (Chulvi, Mulet, and Gonzalez-Cruz, M., 2012).  This should be a function of the expected frequency of occurrence of a combination of properties, the cost of implementing that combination, and the effectiveness of that combination for military purposes.  To aid “conceptual blockbusting”, we do not need precise metrics, just realistic ones that can suggest options to consider.  We thus propose a simple model:

 

The rationale is:

·         Infrequent items are more surprising when they do occur.

·         The difficulty of building costly items makes them less of a threat to surprise us.

·         We are only concerned about items that are effective, meaning can cause damage by their speed and armaments.

·         We are especially interested in novel items that are not much like previous items.

 

Frequency can be estimated from the frequencies of the assigned properties by the usual methods for contingency tables.  If we have M properties and  is the frequency of value k of property i out of a population of N items, we can estimate the frequency of the combination using an independence assumption as:

Frequencies of attribute values were estimated from considering how often that value would appear in a real military setting.

Cost is primarily related to quantity, weight, and material, so we need to define a set of materials for vehicles and the associated densities.  There are economies of scale, so we assumed cost was proportional to the square root of the weight.  Similarly, we assumed cost was proportional to the square root of the power as more efficient propulsion can be achieved with increases in scale.  Cost obviously depends on the material and the operational cost depends on the habitat in which the vehicle is operating, and the degree of friction associated with the shape of the vehicle in that habitat, so we had three factors that needed to be set by world knowledge.  We did not include a cost based on frequency; cost varies inversely with frequency when nations must buy technology from a fixed budget, but this is not necessarily the case when national pride or perceived capability gaps drive technology purchases.  We assumed that passengers were not needed in the vehicle given the increasing use of autonomous vehicles, so we do not need to include the cost of space for them.

Novelty relates to the similarity of the item to a universe of other items.  In this case, we can measure novelty as the distance between the item and the most-similar thing we have postulated before.  Since the numeric measures are generally on logarithmic scales, we take the absolute value of the difference of their value to measure their contribute to the distance; for nonnumeric measures, we had best success by assigning a distance of 2 to values that are different and 0 to the values that are the same.  We used the sum of the absolute values of the distance components (the L1 metric) to measure distance so as to not overweight any one feature due to a large discrepancy in its values.

Effectiveness is a more difficult concept to formulate because it depends on the goal of the vehicle, and there are several kinds of very different goals.  For this demonstration system, we multiplied five factors:

·      A function of the maximum speed of the vehicle computed using  and then a logistic function with mean 0.0001 and slope 10000 applied to the square of the maxspeed.  This models the increasing damage potential with the kinetic energy of the vehicle, leveling off when total destruction of a target is highly certain.

·         The compatibility of the mass with the volume, measured as the minimum of the ratio and its reciprocal.

·         The compatibility of the weight with the power, measured as the minimum of the ratio and its reciprocal.

·         The effectiveness of the material for military use; steel and composite materials are better.

·       where count is number of occurrences of the vehicle.  This models the target destruction by a set of independent shots as a Bernoulli process with one independent draw for each vehicle.

This model assumes that attack is the purpose of the military vehicle, but intelligence gathering would favor a different formula where low weight and lack of visibility are more important.   Logistic functions were used when necessary to prevent any one factor with a very high or very low value from overriding the others.

4.     Experiments

We implemented a demonstration system in the Python programming language using evolutionary computing.   Most of the program runs described took a few minutes on a standard workstation. 

 

4.1. Implementation issues

Our implementation started with an initial database of random solutions, and used mutation and crossing operations to create better solutions.  Mutation for our implementation meant changing one feature of a solution to something else; crossing meant finding two solutions, selecting a feature, and either averaging the feature if numeric or replacing with the value of the feature in the other solution.  One mutation and one crossing were added to the agenda at each step.

We used the fitness measure described in the previous section.  Solutions were stored in a data structure sorted by decreasing values of their fitness rating.  Items chosen for mutation and crossing items were selected by a biased random sampling where their probability of choice was proportional to their rating.  Novelty values change every time something is added to the agenda, but this calculation is time-consuming so we had a parameter that determined how often recalculation is done.  At the same time as recalculation, we also prune the agenda of the weakest items (“clean it”) according to a percentage specified when running the program.  Experiments varied the size of the randomly selected starting agenda, the number of steps involving mutations and crosses, and the frequency of recalculation of the novelty function, and the fraction of the lowest-rated items of the agenda that were removed at each recalculation. 

 

4.2. Results

The following shows the top-rated items in terms of surprise from a random run.  Items listed in order are the rating, weight, volume, power, turn radius, count, material, habitat, and shape.  So for instance the top-rated item is a new steel plate in space of weight of 10kg, volume of 125 cubic meters, power of 1 hp, and a turn radius of 1 meter.

 

rating 18.70723455921 | 10.0 kg | 125.0 m^3 | 1.0 hp | 1.0 m | 1 count | steel | space | plate | new

rating 18.402007498956 | 10.0 kg | 11.18 m^3 | 10.0 hp | 1.0 m | 1 count | plastic | water_surface | plate | new

rating 15.086991435078 | 10.0 kg | 1.0 m^3 | 3.16 hp | 1.0 m | 1 count | steel | water_surface | plate | new

rating 13.691803245446 | 50.0 kg | 0.2 m^3 | 1.0 hp | 2.0 m | 1 count | plastic | water_surface | plate | new

rating 10.855962992669 | 10.0 kg | 1.0 m^3 | 3.16 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 9.770710464565 | 10.0 kg | 1.0 m^3 | 10.0 hp | 1.0 m | 1 count | plastic | water_surface | plate | new

rating 9.365561076968 | 10.0 kg | 1.0 m^3 | 10.0 hp | 1.0 m | 3 count | wood | water_surface | plate | new

rating 7.006564892908 | 250.0 kg | 1.0 m^3 | 10.0 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 5.556906285205 | 10.0 kg | 1.0 m^3 | 31.62 hp | 1.0 m | 1 count | plastic | water_surface | plate | new

rating 5.439908656362 | 10.0 kg | 0.2 m^3 | 1.0 hp | 1.0 m | 1 count | steel | air | plate | new

rating 5.169972413708 | 50.0 kg | 0.2 m^3 | 10.0 hp | 8.0 m | 1 count | steel | water_surface | sphere | old

rating 5.103560523031 | 50.0 kg | 0.2 m^3 | 3.16 hp | 2.0 m | 1 count | plastic | water_surface | plate | old

rating 4.676808639803 | 10.0 kg | 125.0 m^3 | 1.0 hp | 1.0 m | 1 count | steel | air | plate | new

rating 4.422056018388 | 50.0 kg | 25.0 m^3 | 10.0 hp | 8.0 m | 1 count | plastic | water_surface | sphere | usedsome

rating 4.331147160231 | 50.0 kg | 0.2 m^3 | 10.0 hp | 2.0 m | 1 count | plastic | water_surface | plate | old

rating 4.317507435347 | 10.0 kg | 125.0 m^3 | 100.0 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 4.095362697204 | 10.0 kg | 0.2 m^3 | 1.0 hp | 2.0 m | 1 count | plastic | pavement | ship | new

rating 4.071435199301 | 10.0 kg | 1.0 m^3 | 100.0 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 4.045361025754 | 10.0 kg | 5.0 m^3 | 1.0 hp | 1.0 m | 1 count | steel | air | plate | new

rating 3.90063370091 | 10.0 kg | 25.0 m^3 | 100.0 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 3.749527706961 | 22.36 kg | 7.48 m^3 | 10.0 hp | 1.41 m | 1 count | wood | water_surface | plate | new

rating 3.692454884378 | 10.0 kg | 5.0 m^3 | 1.0 hp | 8.0 m | 10 count | composite | pavement | ship | old

rating 3.592518375636 | 50.0 kg | 5.0 m^3 | 100.0 hp | 2.0 m | 1 count | steel | pavement | box | new

rating 3.486476484546 | 10.0 kg | 1.0 m^3 | 10.0 hp | 1.0 m | 1 count | wood | water_surface | plate | new

rating 3.208415778956 | 250.0 kg | 5.0 m^3 | 1.0 hp | 4.0 m | 1 count | steel | space | plate | old

rating 3.187507536258 | 50.0 kg | 25.0 m^3 | 1.0 hp | 4.0 m | 1 count | steel | space | plate | old

rating 3.124941999001 | 10.0 kg | 1.0 m^3 | 100.0 hp | 1.0 m | 1 count | plastic | water_surface | plate | new

rating 3.028154663256 | 10.0 kg | 0.2 m^3 | 10.0 hp | 8.0 m | 1 count | steel | water_surface | sphere | usedsome

 

One advantage of evolutionary computation over neural nets is that it is easy to modify the parameters to test out theories.  So if we think plates were too popular in the output, we can increase the cost of plates and run again.  Similarly, if we want to focus on the water surface, we can eliminate the other possibilities from the choice lists and run again.  Since random choices are made, new runs with identical parameters will have a few differences but we rarely noticed significant ones.

Figure 1 shows a plot of agenda size in items (horizontal axis) versus average distance of an agenda item from its nearest neighbor (vertical axis) for runs with cleaning the agenda (removing the worst items).  Colors indicate runs involving each set of parameter values that was tested.  The parameter values used for the runs and listed in the lower right are the size of the starting agenda, the number of items added to the agenda by the evolutionary algorithm, the number of steps between each recalculation of the nearest agenda item which was used by the “novelty” factor, and the weight on nonnumeric attributes in computing distance (numeric attributes were compared using the difference between their logarithms).  There are two points vertically for each agenda size, one for the average distance before recalculation and one for after.  Points towards the upper right mean a more complete agenda than points to the lower left because both larger nearest distance and agenda size are desirable.

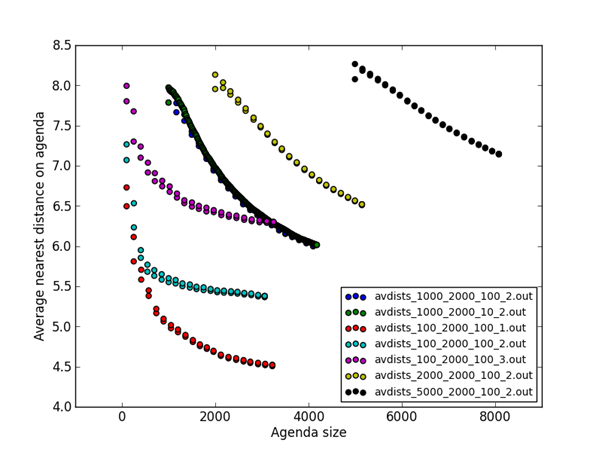
Figure 1: Average distance of nearest item on the agenda versus agenda size, with no agenda cleaning.

Table 1 shows the highest ratings found for the data in Figure 1 plus a few more runs.  Some observations: 

·         It appears that a larger number of starting items is desirable, since average distances stay high and do not decrease for quite a while for larger values.  Starting items are randomly generated so a larger starting number means the space of possible vehicles starts as more representative, and that apparently helps when good offspring are desired.  It looks like 2000 was the best number of starting items because both 1000 and 5000 gave lower numbers for maximum rating, though that for 5000 can be discounted somewhat because the agenda was larger.

·         The number-of-offspring parameter determines when to stop, but didn’t provide any additional insights.

·         The parameter for the number of items to add before recalculating novelty did not show much effect in the figure, but improved the final ratings shown in the table.  Apparently recalculating frequently reduces the number of poorer choices added to the agenda, improving overall results.

·         Weight on the nonnumeric factors affected the overall distance calculation and could increase or decrease its values, but varying it did not seem to improve the value of the results.

 

 

 

 

 

 

 

Table 1: Highest ratings found for typical runs.

 

 

Better performance means higher points in the Figure since the goal of our program is to find surprises not like existing examples.  As can be expected, changing the weight on nonnumeric factors in the distance formula increased calculated distances but did not change the shape of their curves.  The difference between average distances before and after recalculation was small, especially after the first one in each run.  The points that appear to form a solid line are from frequent recalculation, and comparing them to the points underneath suggests that frequent recalculation helps only a little.  The most interesting effect, however, is the size of the starting agenda used.  Larger starting sizes resulted in larger average distances (better spacing of the final results) even though items were more crowded in the search space.  This suggests that the space of reasonable possibilities is quite a bit larger than 1000 for this problem (of the 1,392,400 possible combinations), and that it is important to seed the evolutionary algorithm with a diversity of starting vehicles so it can explore better the search space.

Figure 2 shows the results of running with cleaning the agenda the fraction of items having the worst ratings at the same time as the recalculation of the novelties.  Runs started where the points are spaced out and finished where the points are bunched together (indicating approaching an equilibrium where an equal number of items are added and removed).  Pruning the agenda permitted agenda sizes to decrease with time in some cases.

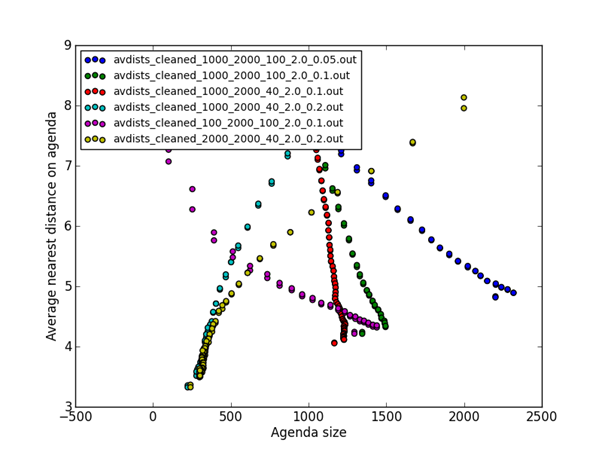
Figure 2: Average distance of nearest item on the agenda versus agenda size, with agenda cleaning.

 

Table 2 shows a summary of the average quality of the best 100 items on the agenda at the termination of each run shown in the figures where 2000 items were added to the agenda.  There was a modest improvement when a larger starting size was used, as a larger average quality means more diversity.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Table 2: Average quality of the top items found for various parameters.

Average quality	Best items averaged	Final agenda size	Agenda cleaning	Starting agenda size	Rebalancing rate	Non-numeric weight	Fraction removed per cycle
3.441	10	2091	cleaned	1000	100	2	0.05
3.483	10	1210	cleaned	1000	100	2	0.1
3.48	10	1107	cleaned	1000	40	2	0.1
5.011	10	178	cleaned	1000	40	2	0.2
3.302	10	1165	cleaned	100	100	2	0.1
4.996	10	192	cleaned	2000	40	2	0.2
3.506	10	4099	uncleaned	1000	100	2	0
3.506	10	4099	uncleaned	1000	100	2	0
3.731	10	4177	uncleaned	1000	10	2	0
2.255	10	3224	uncleaned	100	100	1	0
3.109	10	3060	uncleaned	100	100	2	0
3.754	10	3250	uncleaned	100	100	3	0
4.096	10	5144	uncleaned	2000	100	2	0
3.489	10	8079	uncleaned	5000	100	2	0
2.278	100	2091	cleaned	1000	100	2	0.05
2.576	100	1210	cleaned	1000	100	2	0.1
2.689	100	1107	cleaned	1000	40	2	0.1
3.442	100	178	cleaned	1000	40	2	0.2
2.414	100	1165	cleaned	100	100	2	0.1
3.379	100	192	cleaned	2000	40	2	0.2
2.354	100	4099	uncleaned	1000	100	2	0
2.354	100	4099	uncleaned	1000	100	2	0
2.4	100	4177	uncleaned	1000	10	2	0
1.67	100	3224	uncleaned	100	100	1	0
2.172	100	3060	uncleaned	100	100	2	0
2.565	100	3250	uncleaned	100	100	3	0
2.495	100	5144	uncleaned	2000	100	2	0
2.521	100	8079	uncleaned	5000	100	2	0

5.     Using evolutionary computing in technological-surprise analysis

How can this approach address the problem of military technological surprise?  It can provide a list of possible surprises that can be inspected in a conceptual-blockbusting approach (Adams, 2019).  For each of the high-rated options found, inspection needs to consider whether we have the means and technology to counter it under different kinds of circumstances.  Those we cannot counter well should suggest tactics and technology that we need to start investing in today.  One approach is to recruit human experts to assess how they would respond to each of the top-rated threats found by our program.  Some options experts would consider unreasonable, suggesting modifications to the fitness function, but others could be useful.  Those that other experts assess as invoking inadequate responses would suggest development of countermeasures.

Other applications can be addressed with our methodology and program.  We are currently working on a program for identifying surprising cyberattacks. 

6.     Conclusions

Evolutionary algorithms appear to be a good tool to address the problems of “unknown unknowns” as military threats.  It is not difficult to configure, since it only requires a definition of the space of possibilities and a ranking scheme for objects within that space.  It is also quite flexible in addressing many categories of military activity.  Our experiments showed a number of surprising results that would provide decision-makers with challenges.  These methods should be part of the strategic-planning and tactical-planning toolkits.

We also explored the ideas in the Libratus poker-playing program, and concluded they did have some application to military mission planning.

7.     References

Adams, J. (2019).  Conceptual blockbusting: A guide to better ideas, fifth edition.  New York: Basic Books.

Beidel, E., (2012, March).  Teams look to crowd-source military vehicle design.  National Defense, Vol. 96, No. 700, p. 15.

Besold, T., Schorlemmen, M., and Smaill, A. (eds.) (2015).  Computational creativity research: Towards creative machines.  Amsterdam: Atlantis Press.

Chulvi V., Mulet, E., and Gonzalez-Cruz, M. (2012).  Measures of product creativity: Metrics and objectivity.  DYNA, Vol. 81, No. 1, pp. 80-89.

Conrad, J. (2017).  Gambling and war: Risk, reward, and chance in international conflict.  Annapolis, MD, US: Naval Institute Press.

De Jong, K. (2006).  Evolutionary computation: A unified approach.  Cambridge, MA, US: MIT Press.

Eiben, A., Smith, J. (2015).  Introduction to evolutionary computing, 2nd edition.  New York: Springer.

Erbele, B. (1996).  Scamper: Games for imagination development.  Waco, TX, US: Prufrock Press.

Fogel, D., Hayes, T., and Johnson, D. (2006, July).  A platform for evolving intelligently interactive adversaries.  Biosystems, Vol. 85, No. 1, pp. 72-83.

Gravia, D., and Loiacono, D. (2015, October).  Procedural weapons generation for Unreal Tournament III.  IEEE Games Entertainment Media Conference, Toronto, ON, CA.

Handel, M. (1987).  Technological surprise in war.  Intelligence and National Security, Vol. 2, No. 1, pp. 1-53.

National Research Council (2009).  Avoiding technology surprise for tomorrow’s warfighter: A symposium report.  Washington, DC, US: National Academies Press.

National Research Council (2013).  Responding to capability surprise: A strategy for U.S. Naval forces.  National Academies Press, retrieved August 18, 2019 form www.nap.edu.

Petrov, V. (2019).  TRIZ: Theory of inventive problem solving.  Chaum SU: Springer.

Richardson, D. (2001).  Stealth warplanes.  London: Salamander Books.

Rice, A., McDonell, J., Spydell, A., and Stremler, S. (2006, May).  A player for tactical air strike games using evolutionary computation.  IEEE Symposium on Computational Intelligence and Games, Reno, NV.

Ruchl, C. (2019, January 20).  Why there are no nuclear airplanes.  Retrieved from https://www.theatlantic.com/technology/archive/2019/01/elderly-pilots-who-could-have-flown-nuclear-airplanes/580780/.

Sahan, E., and Spears, W. (eds.) (2004, July).  Swarm robotics: Proc. of the SAB Workshop.  Santa Monica, CA, US, in Lecture Notes in Computer Science, Vol. 3342, Springer.

Shah, J., Vargas-Hernandez, N., and Smith, S. (2003).  Metrics for measuring ideation effectiveness.  Design Studies Vol. 24, No. 2 , pp. 111-134.

Tiao-Ping, F., Yang, B.-D., Chen, J.-H., and Li, G.-Q. (2010, May).  Operational experiment based on artificial life modeling.  2^nd Intl. Conf. on Modeling, Simulation, and Visualization Methods, Sanya, China.

U.S. Department of Defense (2001, January 9).  USS Cole Commission Report.  Retrieved from https://www.hsdl.org/?view&did=441810.

8.     Appendix A: Preliminary analysis of the unknown-unknowns problem

The efficacy of a new idea is the more important of the two qualities. Anybody can come up with a new idea for an attack, but only those ideas which cause damage are of interest. Thus, the problem of unknown unknowns can be addressed by systematically developing interesting vehicles

An evolutionary algorithm (EA) is a machine learning optimization algorithm based on the Darwinian principle of survival of the fittest. One wishes to optimize a function, called the fitness function. One can measure the efficacy of an arbitrary set of inputs to the function. An EA begins by generating random solutions to the fitness function. The elites of a generation are the fittest individuals. The elites have children, which are solutions that combine random qualities of the elites. A new generation is formed from the elites and their children. Their fitness is measured, a new elite emerges, and the process begins anew. Eventually, the algorithm ends and the fittest solutions are a good approximation of the optimal solution to the function. 

An evolutionary algorithm is suited for the problem of UUID because the randomness of the initial population is a good approximation of innovation, and an appropriate fitness function could measure interest. 

A solution to UUID is a method for discovering innovative, interesting vehicles, where innovative means not seriously considered in the past, and interest is a measure of the ability of a vehicle to cause trouble. It makes sense to use an AI to search through the space of vehicles because a human has a hard time dealing with such a vast space. It makes sense to use an EA because randomness will cover a wide range of vehicles. However, a computer has a limited understanding of reality, so it makes sense to include human judgement in the solution. Thus, the solution presented in this paper is an augmented creativity machine. That is, a computer comes up with interesting, new vehicles, and a human decides whether those vehicles are relevant to the problem at hand. 

A vehicle is defined in terms of its characteristics. The algorithm inputs a number of primary characteristics from which all other vehicle characteristics may be derived. Each characteristic is a rating from 0-100, where a high rating represents excellence. Primary components are analogous to the primary colors red, yellow, and blue, from which all other colors are derived. Thus, the primary components must be characteristics fundamental to all relevant vehicles. The primary characteristics used in our algorithm are: mass, volume, speed, acceleration, and maneuverability.

The derived characteristics are those that matter to the interest rating. Interest is a heuristic rating, that is, it is purely subjective based on the situation. From the primary characteristics we derive less apparent characteristics, which are combined in a mathematically coherent way to provide an interest rating. In this paper, we suggest an interest rating meant to capture some fundamental properties of interesting vehicles: cost, purpose, and feasibility. 

An interesting vehicle is one that is possible to build, thus feasibility is an important factor to consider. Anybody can come up with a dangerous and innovative vehicle, but we don't care unless it's actually possible to build. For example, a tiny, super massive vehicle is very interesting because it could be filled with many explosives, or could be made from a strong material, but we are unlikely to encounter such a vehicle. Such a vehicle would thus have a low feasibility rating. The feasibility rating rewards vehicles for having combinations of characteristics that are likely to be possible to combine. 

The set of possible things that a vehicle can excel at is captured in the purpose rating. Various combinations of primary characteristics contribute to different human defined purposes. For example, a very massive vehicle probably has a different purpose than a very fast vehicle, but a human has to describe how a given purpose relates to a given characteristic. The purpose rating is meant to inform the human about the likeliest use of a combination of characteristics. The interest scales with the purpose because interesting vehicles tend to excel in a single area, especially because the purposes should be different enough to capture a wide range of possible vehicles. The three purposes used in our algorithm were: explode, guns, and sneaky. 

The last derived characteristic is cost, which scales inversely with interest. Cost captures the difficulty of making marginal improvements to any primary characteristic, with different growth functions heuristically assigned to different characteristics. Cost is a catch-all metric for ensuring that vehicles are properly incentivized to diversify their characteristics. A vehicle with high rankings in all categories is very interesting, but an elite all-purpose vehicle is not realistic because such a vehicle is prohibitively difficult to construct. Cost not only reigns in the interest rating of super-vehicles, but provides the human with a prediction of the relative likelihood of a vehicle. 

Our cost function grew linearly with mass and volume, but exponentially with speed, acceleration, and maneuverability. The reason being that the last three characteristics are harder to improve than the first two characteristics.   Input will be the primary characteristics that describe some fundamental properties of relevant vehicles.  An evolutionary algorithm will combine primary characteristics in such a way to describe vehicles with high interest ratings.  Interest will be defined in terms of derived characteristics that rewards vehicles that (1) can be built, (2) do something important, and (3) focus on a single area of innovation.  Output will be a list of vehicles with high interest, along with their cost, purpose, and feasibility.  A human can take into account the derived qualities and the final interest rating to make a decision as to the intangible danger of such a vehicle.

The algorithm is generalizable to any situation is which (1) we can describe the fundamental components of vehicles so that basic components should be ones that can be identified by the usual techniques (vision, radar, etc.), and (2) fundamental components can be related to interesting characteristics.  The algorithm is useful in any situation in which we broadly know what to be worried about, and we know broadly what kinds of characteristics are utilized by vehicles of interest. The adaptability of the program is its main strength. It also provides a systematic way of detecting innovation in the area of combat identification. 

Heuristically defined characteristics run the risk of being inaccurate. A human is defining everything, the computer is only reducing the combinatorial difficulty of the problem to aid the human. Thus it is important to have an accurate model. However, the heuristic nature of the program is also a strength, because it allows it to capture the subjective nature of creativity. 

 The other weakness is that it is not truly creative. A human must provide some of the creativity, which is not a given. For example, it is reasonable to expect that such an algorithm could have predicted that a small, light boat filled with explosives would be very interesting, but a human would have had to make the creative jump to realizing that such a boat could be driven up to a battleship to inflict significant damage. 

The US is very interested in predicting effective enemy innovations in the area of combat vehicle identification. Exploring the vast space of possible innovations requires a machine. A large number of possible vehicle characteristics are inputted into an evolutionary algorithm. Combinations of characteristics are bred until elite vehicles emerge, where elite is defined in terms of some heuristically derived function based on the primary characteristics. The products of evolution are inspected by a human for their relevance to the identification problem at hand. The general description of interesting vehicles is hopefully adapted to the specific situation at hand, and an innovative vehicle is identified before its deadly purpose is discovered through experience. 

9.     Appendix B: Analysis of the Libratus poker-playing AI program

Libratus is an algorithm developed at Carnegie Mellon for solving Heads Up No Limit Texas Hold 'em (HUNL), a poker variant with no limit on bet size played between two players. In 2017, Libratus utterly defeated four top professional HUNL players in a twenty day tournament by a very statistically significant margin. Not only was this the first time that humans had been defeated by a machine in HUNL, but Libratus also handily beat the other top poker artificial intelligence algorithms. In fact, the strategy devised by Libratus so closely approximates the optimal that poker is now considered to be solved. 

The goal of Libratus's algorithm is to approximate a Nash Equilibrium Strategy (NES). Generally, a Nash Equilibrium of a game is a set of actions for each player such that neither player can gain by changing their strategy. A strategy is that set of actions, along with the frequency with which one plays them, for each game state (cards in hand, cards in play, and pot size are the aspects of a game state). Thus, the NES is a set of actions at each possible game state such that opponents break even with perfect play. Libratus aims to play perfect defense: if the opponent plays perfectly, the game is a tie, but any mistake will cause the opponent to lose in expectation. 

Solving HUNL is a milestone in game-playing artificial intelligence (AI) because HUNL is a vastly complex imperfect information game. Imperfect information games are games where neither player knows exactly which game state they are in, because their opponent is hiding some information. Compare to perfect information games, where the true game state is known to both players i.e. the true game state does not differ from the perceived game state. Imperfect information games often better model the world than perfect information games because most of the time we don't know everything about a situation, but we still need to devise a strategy. 

The techniques Libratus uses to determine an NES in a poker game could be generalized to apply to military mission planning because both are imperfect-information games. The military must develop a strategy that takes into account the many possible adversarial actions, without knowing which of those actions the adversary will take. If the real world can be modeled in a way that Libratus can understand, then Libratus can develop a strategy for the model applicable to the real world. Libratus the best bet for determining how to navigate an imperfect-information game related to military mission planning. 

Libratus is in a unique position to revolutionize the way that the military plans its missions because Libratus outputs adversarial strategies. Without Libratus, one has to develop a strategy based on a, not always accurate, assumption about the way an opponent will act. With Libratus, one need not assume. Instead, Libratus will output a strategy profile for the opponent and an optimal counter-strategy, using as input the possible adversarial actions. Development of Libratus would inform the military about what to expect from adversaries and how best to act.

An important feature of poker is the ability to bluff (Conrad, 2017), and this has many military applications.  The Soviet Union, for instance, bluffed in regard to having nuclear-powered military aircraft (Ruchl, 2019).  So not all candidates found with our program will be seen.  Nonetheless, preparedness for situations that are never encountered is common and expected in military organizations and is not a waste of resources.  Bluffing can also be useful as a strategy defensively, meaning in this case for us to give the appearance of having a technology we actually do not.  The best technologies for this are just those for which an adversary would compute a high surprise value, so our framework in this paper provides a basis for choosing them. 

 

9.1. Libratus strategy

Libratus aims to mitigate the astronomical computational complexity of HUNL with a three-pronged machine learning algorithm. Libratus uses an abstraction of poker, To reduce the complexity of the game, to determine a blueprint strategy before the game. An abstraction of poker is a game with the same rules as poker, but bet sizes and card combinations close in value are treated the same. Libratus learns while it plays by using an algorithm called Nested Endgame Solving (NEGS) that solves a more finely detailed abstraction as it encounters game-states further down the tree in real time. After play, Libratus updates its blueprint strategy with strategies it encountered while playing. Since HUNL is too big for Libratus to consider every possibility to its full extent, it must decide which possibilities are the most important to consider to their full extent. 

 

9.1.1        MCCFR - improved by skipping negative regret

MCCFR is a self-play algorithm that solves an abstraction of poker. The researchers decide upon an abstraction and program it into Libratus. Libratus then uses that abstraction to devise a strategy called the blueprint strategy. MCCFR uses two types of abstraction:

1.      action abstraction - the most common actions taken by AI in a previous tournament are included in the game tree, and off-tree actions are mapped to a closely related action in the tree. Example: bets of $100 and $101 are treated as the same.

2.      card abstraction - similar hand values are treated as the same.  Example: the same strategy is developed for ace-high flush (included in the abstraction) as for king-high flush (not in the abstraction) for every game state i.e. it pretends that the king is an ace, but does not pretend that the ace is a king.

MCCFR minimizes regret, a quantity representing how much better things would have turned out with a decision other than the one chosen. By playing itself billions of times, Libratus determines which actions it regrets the least, and then makes those actions with higher probability. The key improvement over previous AI is called Regret Based Pruning (RBP): paths with very negative regret are visited less often (conversely, positive regret means you liked the action, negative regret means you disliked the action). RBP frees up computational space, allowing for a more detailed abstraction to be made, further mitigating the issues with abstraction. 

Initially, MCCFR assigns regrets to two players uniformly distributed about their actions. One player is chosen to update their regret, while the other holds their regret constant. At each decision point, the player updating their regret plays each action that it can, depth-first. Eventually, the game ends and a reward is passed up, which updates the regret of each action. The actions with high reward are updated to be played more often, and vice versa. Then, the roles are reversed. MCCFR guarantees that the regret for any action approaches zero as the number of games approaches infinity. That is, the strategy improves as more games are played. 

 

9.1.2        Nested Endgame Solving (NEGS)

HUNL is so big (10^161 decision points, compare to 10^80 atoms in the universe) that most actions cannot be included in the abstraction (abstraction has 10^12 decision points). Thus, MCCFR is non-optimal for most game states, but provides a good baseline, and is sometimes optimal. The blueprint strategy calculated by MCCFR is decreasingly optimal as the game progresses, because the number of decision points grows. Even so, MCCFR can reliably be used in the first two betting rounds. A better strategy can be computed to replace the original blueprint in the last two rounds by developing a more finely detailed blueprint than used in the first two rounds. The process of developing the strategy for the last two betting round subgame is called Nested Endgame Solving. 

NEGS assumes that the opponent is dealt a random hand, and that Libratus has played according to the blueprint before reaching the subgame. At this point there is a probability distribution over the types of hands that Libratus could have, because each subgame has various bet sizes and community cards which influence the likelihood of certain hands being folded. Libratus then deals itself a random hand according to this distribution. The opponent can choose to enter the subgame or not. 

If the opponent chooses to enter the subgame, Libratus uses a variant of counterfactual regret minimization particularly suited to small size games called CFR+ to calculate the NES. The subgame NES is guaranteed to be more accurate than the blueprint NES because the subgame is more detailed than the blueprint abstraction. Alternatively, if the opponent chooses to not enter the subgame, then the augmented subgame ends. However, according to the blueprint, not entering the subgame is awarded a value less than or equal to entering the subgame, because the opponent should enter the subgame according to the blueprint NES. Thus, the opponent can enter the subgame and play against a fine-tuned NES, or the opponent can make a non-optimal decision according to the blueprint, at which point Libratus will solve a new subgame. 

Libratus's NEGS algorithm improved over previous subgame solving techniques in four areas:

·         Constructs a new subgame every time the opponent makes a bet i.e. no abstraction for bet sizes.  Mitigates rounding error from clumping in bets. Previous AI could be exploited by clever opponents who bet amounts on the edge of the abstraction e.g. if a bet of 100 and 150 are treated as the same, then always bet 100. 

·         Using estimates found in the blueprint rather than upper bounds.  Previous AI used upper bounds on subgame expected value (EV) to bound exploitability. The researchers behind Libratus were able to prove that the blueprint EV estimates were close to true EV in a way that allowed them to bound exploitability anyway, rendering the upper bounds excessive. 

·         Probabilistically skipping over very low expected value hands to free up computational space for a more detailed abstraction.  Past techniques ensured that the new strategy for the subgame made the opponent no better off in that subgame for every situation. The new method takes into account that certain situations would require a large mistakes from the opponent, and deems them less likely. 

·         Randomly adjusts bet sizes for unpredictability.  Conceals the NES by betting differently in identical situations.

After the play has concluded for the day, Libratus learns from the decisions made throughout the day.  Data about adversarial decisions allows Libratus to hone areas of the blueprint strategy most likely to be encountered and areas most in need of improvement. Against any given adversarial strategy profile, there is an exploitation strategy, different from the NES, that will perform better than the poker NES. Previous AI would self-improve by adjusting the blueprint to include exploitation strategies deemed effective through data analysis of opponent play. However, this strategy is susceptible to exploitation by an opponent, as it is not a NES. To avoid being exploited by trying to exploit, Libratus only adjusts the blueprint strategy in a way that is still guaranteed to not lose in expectation, even at the cost of gaining less against predictable opponents. 

 

9.2.Why is Libratus special

In order for Libratus to solve a game, it must be able to rank actions based on their contribution to the goal of the game. In poker, it is clear that betting certain amounts at certain times wins a certain amount of the time in the MCCFR simulation because Libratus can play the game against itself. Libratus will be able to understand a wargame as long as it can play itself and determine an action hierarchy; the wargame need not have anything else in common with poker. 

Once Libratus is made aware of the rules of the game, it will determine which probability distributions over which actions at which junctures give itself the highest chance to win. It will make this determination based on all possible actions of the opponent. It can do this because there is a clear relationship between making actions and winning, and it is clear that how some actions contribute to winning less than other actions. Fundamentally, Libratus is an algorithm that ranks actions in situations by assigning all actions a rate at which they should be played. 

Libratus does not understand poker the same that a human does. It does not determine that an opponent is bluffing and decide to call the bluff. Instead, it has determined from playing itself billions of times that a certain set of actions played at a certain frequency results in the highest expected value. If the opponent is bluffing and Libratus calls the bluff, it is purely by chance. A human will call that bluff every time, but Libratus has determined that it should only call that bluff with a frequency that awards it an appropriate expected value. 

An example of an action similar to a bluff is camouflaging a building to make it look like a civilian building. In the wargame, Libratus might have two possible actions: destroy the building or not. Libratus will never be able to tell with certainty whether that building is filled with terrorists or civilians. It can only determine the expected value of destroying the building based on a comparison between the gain from killing terrorists and the loss from killing civilians. The output will be the likelihood of the building being full of terrorists (based on some parameter in the wargame like location, size, traffic, etc.) in terms of the expected value of the action of destroying it. 

 

9.3. An example of a wargame Libratus can solve

Goal: Incapacitate the enemy ship with a pre-defined amount of damage.

Landscape: Nodes on a graph - places ships can move.  Two decoys may be placed at the beginning of the game.  Players are given a probability distribution describing where the enemy and decoys are likely to be i.e. players know where the enemy could be, but not exactly where. By moving around, they gain a better idea. 

Actions: Ships have a choice of actions.  Each type of attack can be distinguished by a probability of hit, resulting damage, and the range in nodes.  Some examples:

·         Scanning an area of 10 nodes will reveal enemy ships, decoys, and mines in that area, infinite range.

·         Decoys which return positive on an enemy scan with exponentially decreasing probability as more scans are made, 30 node range.

·         Camouflage hides ship from enemy scans with exponentially decreasing probability as more scans are made, 30 node range (players can camouflage decoys).

·         Mines can be placed on a node that incapacitate a ship that moves there, 1 node range.

Libratus is effective for this game because:

·         Player actions are well defined and contribute meaningfully towards the goal.

·         Actions can be compared to one another after they are made.

·         Actions betray secret information, although it is not always clear what.

·         The game is complex enough that weaker AI is not equally effective.

 

This type of game is useful because it abstracts naval warfare ideas, details of game can be adjusted to better fit reality (e.g. more types of attacks, multiple ways to incapacitate (rather than just damage e.g. energy and health), any number of ships can be included, ships can have different characteristics such as life total, speed, unique weapons.  The NES strategy will take into account unknown unknowns because the goal can be adjusted.  It can determine the location of enemy ships with high accuracy, without engaging mini-goals could be added that represent strategic points (e.g. occupation of a node area gives a ship a power up).  Libratus may favor overlooked strategies.  The power of Libratus is that it can solve a game of this type with essentially an unlimited number of complications given enough time. 

 

9.4. Where the analogy breaks down

Libratus has limitations in that it cannot understand the world.  Solutions may be inapplicable to the real world until an adjustment to the game is made prevent  "unsportsmanlike" or unrealistic exploitation.  For example, Libratus might find that the best strategy is to place mines in a radius around the ship and move around in a circle, which may not be applicable to a naval situation.  Also, warfighters may be unwilling to use surprising strategies that they deem as unlikely to work.

Libratus is not creative since unknown-unknowns will not be described in detail by Libratus.  The challenge will be for humans to describe unknown-unknowns in a way that Libratus can understand.  Libratus can only detect surprising strategies, not novel strategies.  NES depends on the accuracy of the wargame, and actions in game may not encompass all possibilities.  Libratus is not psychological: Some actions it takes into account may not be realistic, it will not take into account retaliation as a motivation unless explicitly defined as an action, it does assume rational opponents, and does not exploit opponents known to be lacking in some area.

 

9.5. Summary of analysis

By solving poker, Libratus asserted itself as the cutting-edge technology for solving imperfect information games. It is uniquely useful for military applications because it gives insight into opposing strategies. However, Libratus has limitations on the type of information it can understand; it can only solve a wargame where the actions, goals, and landscape are clearly defined and related. Fortunately, games of this type are widely applicable to military mission planning.

The solution Libratus creates for a given wargame will be a probability distribution over the possible actions of each player. The distribution will give military mission planners insight into the expected values of various opponent strategies, and exactly what methods should be taken to counteract the opposing strategy. Understanding what an adversary stands to gain from any of their actions is far more useful than assuming they will play the action deemed most valuable because that judgement may be fallacious. Especially because Libratus will also devise a strategy to counteract the adversary regardless of their strategy. 

Libratus is particularly useful because it can understand and rank, in terms of expected value, any action related to the goal. Thus a wide variety of possible threats can be modeled inside a wargame solvable by Libratus. Some examples include:

·         cyberattack - an action widely variable in power and probability to work

·         camouflage - an action disguised to look like another action

·         decoy - a unit disguised to look like another unit

·         modeling cost of an action

Libratus is the most powerful tool available right now to solve imperfect information games. It is revolutionary in that it requires no assumptions about optimal adversary play. If a wargame can be effectively communicated to Libratus, it will inform the military about what kinds of threats to expect, and how to combat them.