Finding optimal paths for autonomous robots can significantly reduce travel or energy costs or the probability of accident compared to other "reasonable" paths. But finding optimal paths requires a thorough and systematic search. Hence developers of real-time robots have usually not attempted to plan optimal paths. We propose a new way to ensure optimality by a thorough preprocessing analysis of the terrain before the robot is sent out. Our approach builds "optimal-path maps" for regions of near-homogeneous traversal characteristics in the terrain, maps that assign a behavioral description, of the best way to reach a fixed goal point, to every point in that region; the behavioral description is simple enough that the optimal direction at any point can be quickly calculated in real time. Then a robot need only determine where it is periodically, and look up this position in the optimal-path map. This paper provides algorithms to construct optimal-path maps for all single isolated homogeneous-cost polygonal regions, a major subproblem of the general problem of constructing optimal-path maps. We do a complete analysis of the four possible situations, and then provide algorithms to construct behavioral regions within the homogeneous-cost regions, once optimal paths have been found for a particular set of starting points, in @O ( n sup 4 )@ time using @O ( n )@ space, where @n@ is the number of vertices in a polygonal model of the terrain as homogeneous-cost regions. Our algorithm greatly simplifies planning of paths through areas of terrain with near-uniform characteristics, allowing a robot to exploit optimal paths but still have significant time for other matters.
This paper appeared in the Proceedings of the IEEE International Conference on Robotics and Automation, Cincinnati OH, May 1990, 1924-1929.
We address here the problem of high-level path planning for an autonomous vehicle, planning for which the size, joint configurations, and dynamics of the vehicle are negligible factors. Two main approaches have been tried for obtaining optimal paths for this problem when traversal costs for all of the space are known. The most common approach ("wavefront propagation") partitions the traversable space into uniform-size cells, and propagates a wavefront from the starting point until it hits the goal point, a wavefront representing cells of near-equal cost from the starting point. This approach is flexible but suffers from disadvantages of space and time wastage, cost calculation inaccuracies, unreasonable jaggedness of the resulting paths, and inability of the resulting path to approach the optimum as the cell size approaches zero [10]. A newer, alternative approach [9,3,10,4] partitions space into irregular regions of near-homogeneous cost, and performs a recursive decomposition of the space into subregions of similar characteristics with respect to path planning, and then plans a path through these meaningful regions. This "weighted-region" approach exploits algorithms of computational geometry [7] as well an analogy to Snell's Law of optics; it can get true optimal paths without any cost errors beyond those of the original terrain representation. The efficiency of the two approaches is not strictly comparable because their complexities are based on different units (the number of cells total for wavefront propagation, and the number of polygonal-region edges for the weighted-region approach); the algorithms of the second approach are more complicated, but they need reason about fewer entities.
But optimal-path plan planning for robots has been justifiably
criticized for requiring too much computation time and being too
sensitive to real-world inaccuracies to work for real robots in a real
setting. The inaccuracy issue is much less a problem for the
high-level planning we are considering in this paper than low-level
planning, since large features of free space rarely change (hills
rarely move), though inaccuracies due to divergence from the planned
path in the real world can be important. The computational cost of
optimal paths remains a serious argument against them, because
optimality necessarily requires careful consideration of all
alternatives, not just some. But the objection to optimal-path
methods would be mitigated if much of the work could be done in
advance. That is, if we can do a careful analysis of the space though
which the robot will travel before it starts, we could store a
compressed form of this analysis in the robot to guide its subsequent
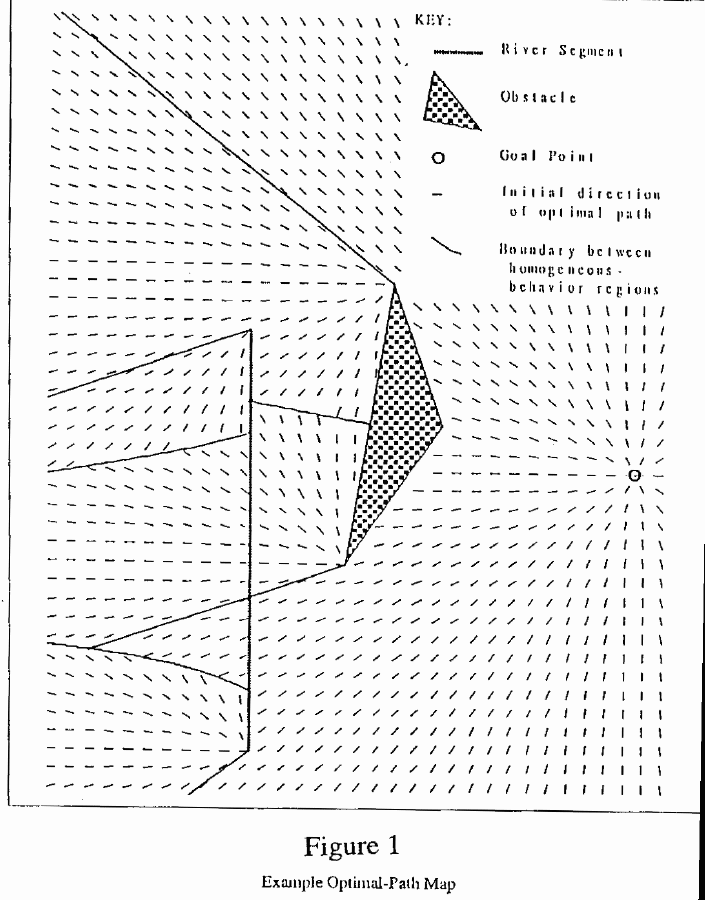
motion. For instance, if we knew what the goal point was, we could
store directions at scattered places in the space, directions
indicating the best way to go to reach the goal from that point
(like the small line segments in Figure 1).
These directions would then form a vector field, an "optimal-path
field," and the robot would just need to follow the field lines to get
there [6]. Then if inaccuracies in path-following by the robot would
cause it to stray from a previously-planned path, it could just look
up the best direction from its new location in an "optimal-path map"
and follow the field direction from there, and so on. And there are
many efficient storage techniques for fields of vectors. Some work of
this sort has been done on "shortest-path maps", where cost is
distance traveled, using a variety of techniques [2,8,5].

Optimal-path maps for a particular goal point can be constructed by
running an optimal-path planner many times for many different starting
points, perhaps for points evenly distributed. But there is a problem
in that the optimal path from a point between those whose optimal
paths you already know may not necessarily be anything like the paths
you already know. For instance, if the optimal paths from points A
and B both go north, the optimal path from point C midway between A
and B could go south if there happens to be a narrow finger of low
cost extending near to C from the south. The problem is lessened if
one picks closely-spaced points to compute optimal paths from, but
there be no guarantee, only a heuristic that the best path from some
point is anything like that of its neighbors. What we need is a
rigorous theoretical basis for being able to say that all points in
some region of space have similar optimal-path behavior, giving
optimal-path maps like Figures 2 and 3. Notice we say "similar", not
"identical", because the latter term rarely applies.
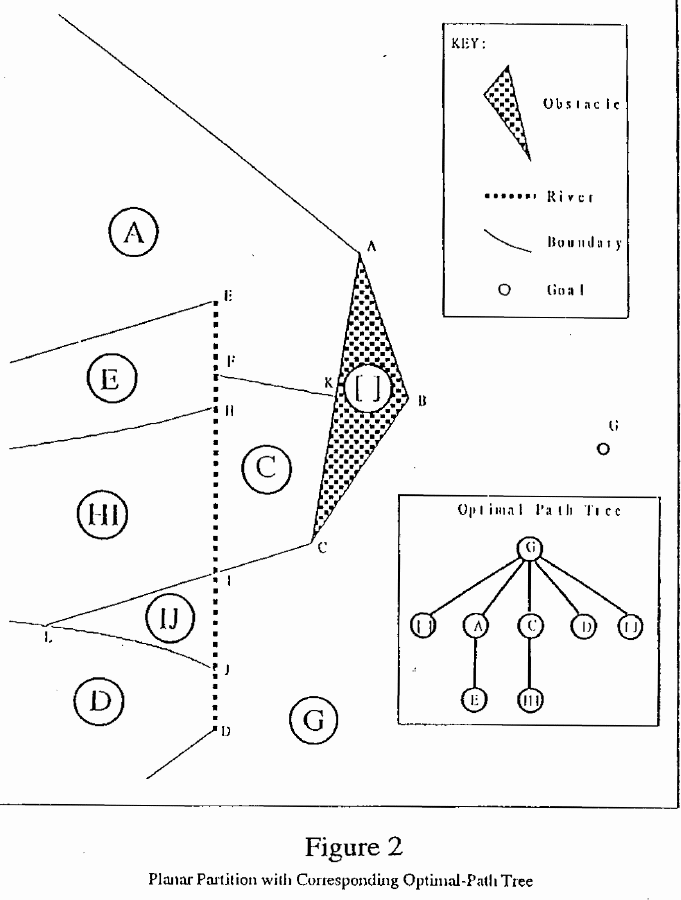
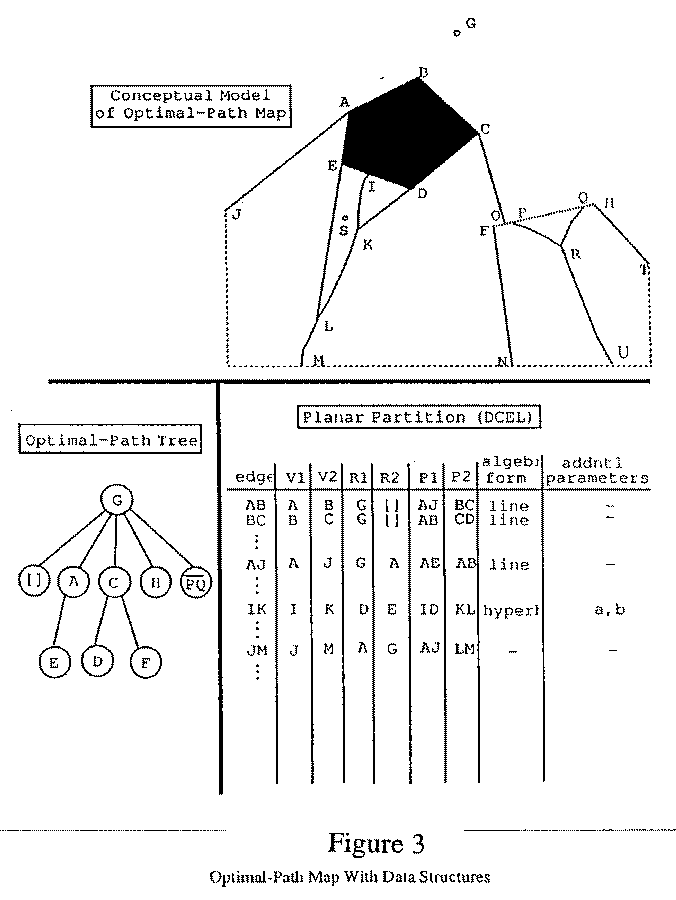
This paper proposes such a rigorous basis for optimal-path maps for regions or areas with homogeneous cost-per-traversal-distance characteristics ("HCAs"). We believe we are the first to make progress on this problem, though we only address "decomposable" HCAs whose analysis can be separated from analysis of their surroundings. Analysis of HCAs is the building block of the weighted-region path-planning algorithms [10,4], enabling us to exploit the previous work on weighted-region path planning. Furthermore, the subproblem has many immediate practical applications itself because large homogeneous areas of near-homogeneous cost arise frequently in applications. For instance, in planning for an autonomous land vehicle, there are grasslands, forests, cultivated fields, and pavement, all areas for near-homogeneous traversal-energy cost. For another example, if a cruise missile is trying to stay close to the ground in hilly terrain to minimize visibility from sensors, there are large areas of air space wherein all points can be seen from the same set of sensors and thus are equally dangerous.
To further simplify the analysis of this difficult problem, we will confine ourselves in this paper to planning across two-dimensional terrain with convex polygonal homogeneous-cost areas (HCAs), where the goal point is known and where the terrain cost characteristics are completely known in advance. (Phenomena such as transportation routes, fences, and impassible obstacles can all be modeled as special cases of HCAs in the limit. And note that world-feature uncertainty does not necessarily imply terrain-cost uncertainty for high-level path planning, since uncertainties can "average out" at a high level of analysis.) We will define connected "behavioral regions" within the HCAs indicating points whose paths to the goal are fundamentally similar in that they cross the same sequence of HCA edges or vertices, or have the same "path list". With this definition of behavioral regions, calculations of the optimal path from any given point in the behavioral region can be quickly done by ray tracing using Snell's law and searching the space of possible departing path directions from the starting point to find the provably convex local optimum of the set of all locally-optimal paths crossing the edges and vertices associated with the behavioral region in the proper sequence. This process is identical to that of finding optimal paths within "well-behaved subspaces" in [9]. To find behavioral regions it is best to focus on their boundaries, places where there are abrupt changes in optimal-path behavior. In this paper we will classify all the possible behavioral-boundary types for single isolated or "decomposable" HCAs. We will analyze and present algorithms for the four possible cases of such HCAs, and then present an algorithm for decomposing certain kinds of terrain into these parts recursively.
We will attempt to summarize in this short paper some complex research; further details are in [1], including proofs of things stated as "Lemma" or "Theorem" without proof here. The ideas proposed here derive from [10] and thus represent a weighted-region-algorithm approach to optimal-path maps; we have also explored three variants of a wavefront-propagation approach, but the output maps always had errors and were unsatisfactory, as described in [1].
The first step in constructing an optimal-path map is to build an optimal-path tree (OPT), a summary of optimal paths from every HCA vertex to the goal. This can be done by a weighted-region path-planning algorithm like [10] or [4].
Define the path list of a path to be the list of HCA-boundary edges and vertices it crosses from the start to the end. Define a visible edge of an HCA to be an HCA edge for which no point on the edge has an optimal-path list whose first element lies on the HCA perimeter. Define a hidden edge as a non-visible edge. A hidden edge may have points whose optimal paths travel through the HCA, which would mean that their optimal paths would have as their first element the visible edge across which they pass. Define opposite-edge sequence as the smallest connected sequence of hidden edges for which the first and last endpoints of the edge sequence have optimal paths whose initial directions follow the HCA edges in opposite (i.e., clockwise versus counterclockwise) directions. If no such endpoint can be found at one end or the other of the sequence of hidden edges, let the endpoint at that end be the "outer" vertex of the last hidden edge, i.e., the vertex which joins the last hidden edge in the clockwise (or counterclockwise) direction with the first visible edge in the clockwise (or counterclockwise) direction.
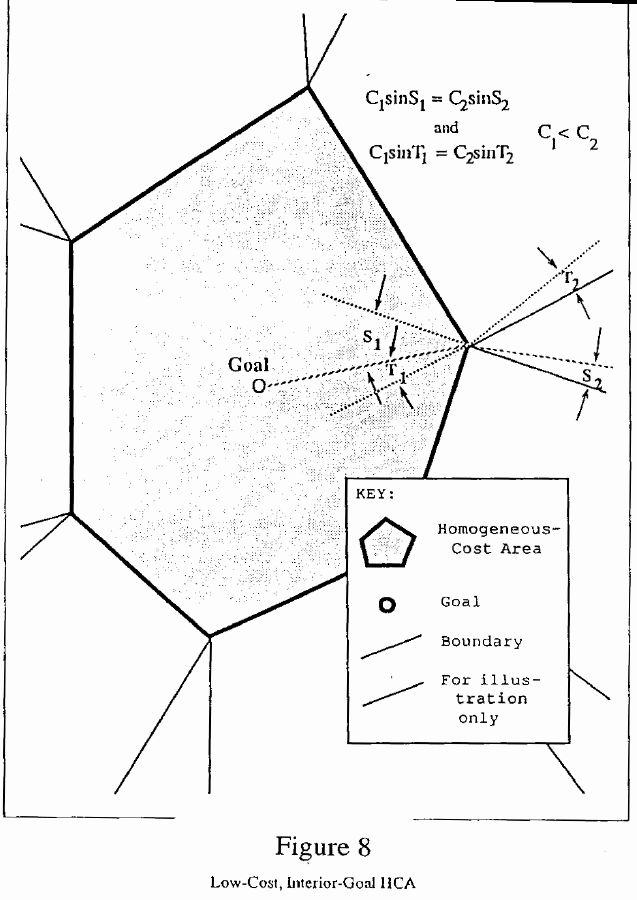
Define the critical angle @ theta sub c @ of an HCA as @ sin sup -1 (c sub 1 /c sub 2 )@ where the @c sub i @ are the unit costs inside and outside the HCA, and @c sub 1 > c sub 2 @. An optimal path crossing an HCA edge will obey an analogue of Snell's Law in optics [3,10] so that for angle of incidence @ theta sub 1 @ and angle of refraction @ theta sub 2 @, and cost rates @ c sub 1 @ and @ c sub 2 @ on either side of the edge, @c sub 1 sin theta sub 1 = c sub 2 sin theta sub 2 @.
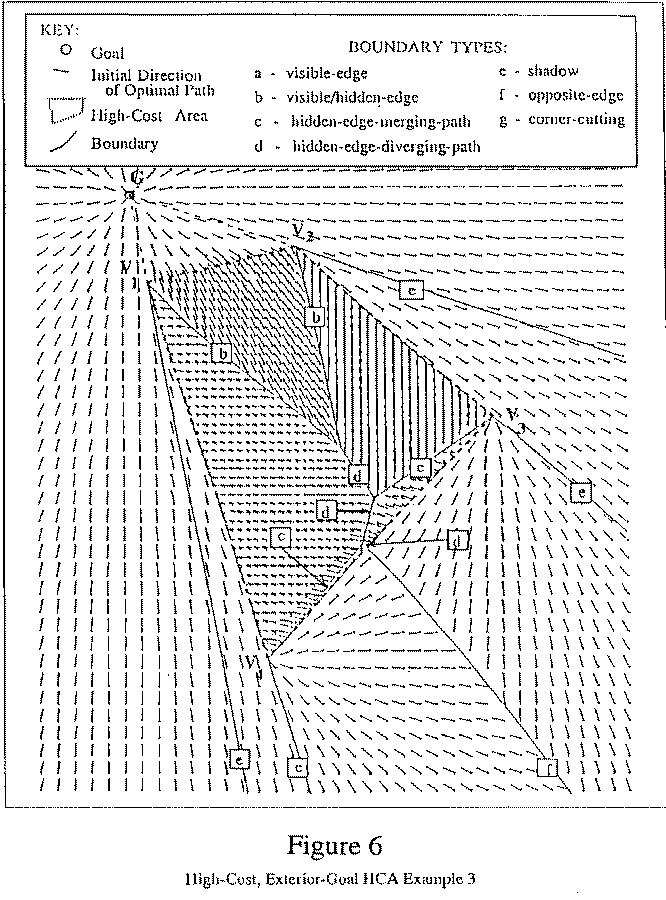
Inside a high-cost HCA with external goal, there are four and only
four types of behavioral boundaries, depending on whether the edges
crossed by paths are visible or hidden (giving three combinations) and
are on the same or opposite sides of the opposite-edge boundary
(giving one additional combination since it only applies to
hidden-edge paths). See Figures 4, 5, and 6. (The small line
segments in the Figures indicate optimal-path directions, but do not
represent information necessary for the algorithms of this paper, and
are only for demonstration; they were computed by running the
path-planning program of [10] from them to goal G.) Each pair of HCA
edges is potentially associated with an interior boundary. A
visible-edge boundary distinguishes optimal paths which go
through two different visible edges; the optimal paths cross their
respective edges according to Snell's Law. The Appendix states the
analytic form of such a boundary. Although not expressible in closed
form, the boundary has much the same shape as a hyperbola segment
which forms an obstacle opposite-edge boundary [5], i.e, it has
positive but decreasing curvature from its point of incidence upon an
HCA vertex inward into the HCA, and this curvature is typically small
so that the curve is almost linear. An example of a visible-edge
boundary is found in Figure 4, labeled a.
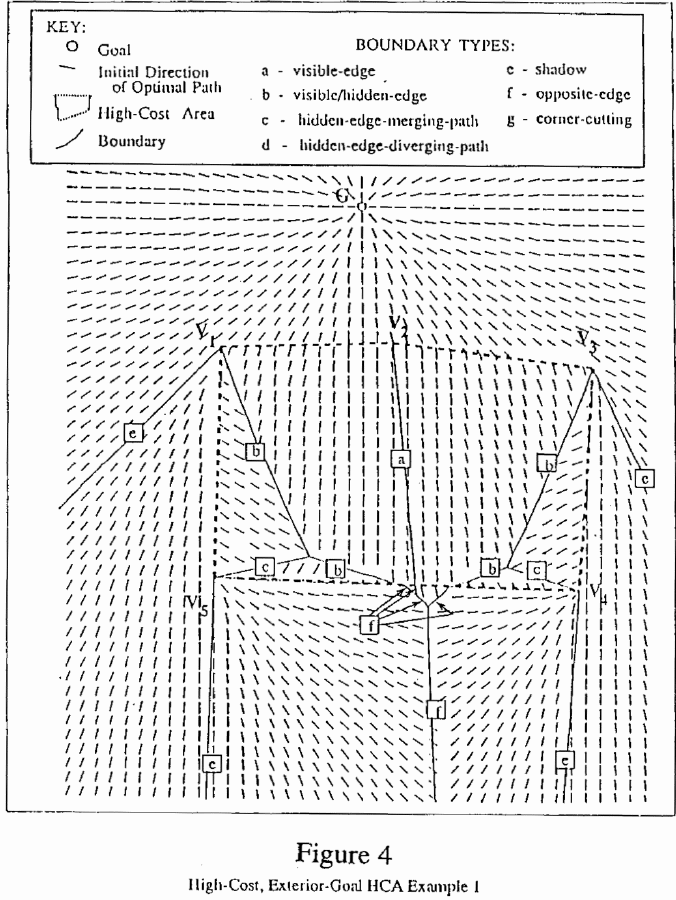
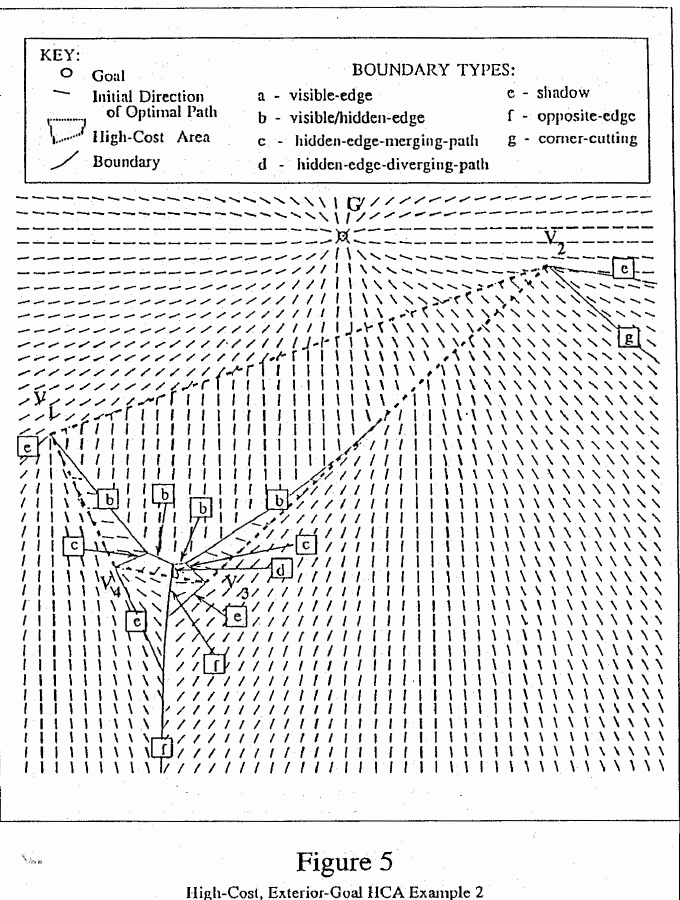
A visible-hidden-edge boundary distinguishes optimal paths going through a visible edge from those going through a hidden edge; the latter paths traverse the HCA edge at exactly the critical angle and the follow the edge. Lemma V-4.2 states the analytic form of this type of boundary, which again is similar to a hyperbola. Examples of this type of boundary occur in Figures 4, 5, and 6 and are labeled b.
A hidden-edge merging-path boundary distinguishes optimal paths leaving the HCA at two different hidden edges at exactly the critical angle, and for which all paths merge before the goal. A way to check for this behavior is to see if an optimal path from a vertex of one of the edges includes a vertex of the other edge. Lemma V-4.3 states the analytic form of this type of boundary, which is a line segment. The boundaries labeled c in Figures 4, 5, and 6 are hidden-edge merging-path boundaries. A hidden-edge diverging-path boundary is like the preceding except the two classes of paths merge only at the goal. This type of boundary is also a line segment, as stated in Lemma V-4.4. Examples of this type of boundary occur in Figures 5 and 6 and are labeled d.
Each pair of adjacent edges is always associated with one of the above interior boundaries, while non-adjacent edges may or may not be. If shortcutting does not occur across an HCA corner, a boundary will start at the vertex at that corner. If shortcutting does occur, the boundary associated with that vertex will intersect the HCA edge at the point where shortcutting starts (see Figure 4 where two of the boundaries labeled b intersect the opposite edge, Figure 5 where one of the boundaries labeled b intersects the lower right edge of the HCA, and Lemma V-4.5). From the vertex or shortcutting point at which such a boundary begins, it will continue into the HCA interior until it intersects another boundary or HCA edge. At the point at which two such boundaries first intersect they will terminate, and a third boundary will begin which represents the division between the two regions which the first two boundaries did not have in common. For example, in Figure 4 the boundary associated with vertex @V sub 1 @ distinguishes paths which cross edge @V sub 1 V sub 2 @ from those which travel along edge @V sub 1 V sub 5 @, while the boundary associated with vertex @V sub 5 @ distinguishes those which travel along edge @V sub 1 V sub 5 @ from those which travel along edge @V sub 4 V sub 5 @ passing through vertex @V sub 5 @. These two boundaries begin at their respective vertices and intersect in the HCA interior, and from that point a third boundary begins which distinguishes paths which cross edge @V sub 1 V sub 2 @ from those which travel along edge @V sub 4 V sub 5 @ passing through vertex @V sub 5 @. These two descriptions (crossing @V sub 1 V sub 2 @ and traveling along @V sub 4 V sub 5 @ through @V sub 5 @) represent the two regions which the initial boundaries did not have in common, so they characterize the third boundary. Boundaries will continue to intersect and new ones begin in the HCA interior until the boundary associated with each visible vertex is joined with one or more hidden vertices or HCA edges (Lemmas V-4.10 and V-4.11).
These networks of boundaries can be represented as trees, where each boundary is considered a node, and edges connect nodes whose boundaries intersect (see Lemma V-4.10). Such a tree, called an interior-boundary tree, has interior nodes with exactly two children, while the root of such a tree can have zero, two, or four children. A tree whose root and sole node has zero children represents a boundary which goes from one edge of the HCA to another without intersecting any other boundaries, such as the boundary emanating from vertex @V sub 2 @ in Figure 4. A boundary separates two regions, and any time two boundaries intersect it must be, as explained above, that they have one of the two regions in common. Beyond the point of intersection, the two regions they did not have in common must be separated by a boundary. Thus each time two boundaries intersect, a third must begin. We choose as leaf-nodes those boundaries associated with HCA vertices, because one boundary is guaranteed to exist for each vertex, and no other interior boundaries intersect it at the vertex or edge, so we can be sure that they will have no children. At the other end of such a boundary it either intersects an HCA edge, meaning its node is a root without children as described above, or it intersects two other boundaries, one of which will also be associated with an HCA vertex and so be another leaf node. If the latter is true, the boundary beginning at the intersection point of the two leaf-node boundaries will serve as the parent node of the two boundaries. This merging of boundaries will continue until the parent node's boundary intersects an HCA edge, in which case the node is the tree's root, or until roots of two boundary trees are found to represent the same boundary, in which case the two trees can be merged into one. This is the case where a root will have four children, representing the two boundaries which intersect each end of the root's boundary.
Outside the HCA, there are only four possible types of boundaries. Again, HCA edges are trivial boundaries (Lemma V-4.5). HCA shadows are defined exactly as for obstacles [5]. Examples of HCA shadow boundaries are labeled e in Figures 4, 5, and 6. The other two types are HCA opposite-edge boundaries and HCA corner-cutting boundaries. HCA opposite-edge boundaries are the generalization of obstacle opposite-edge boundaries, and differentiate between paths which start outside the HCA and go through or around the HCA in different directions. There are three types of opposite-edge boundaries, depending on whether neither, one, or both optimal paths go through an HCA edge. A path which does not go through the HCA goes around it initially via one of its vertices. The case where neither path goes through the HCA is the same as the obstacle opposite-edge boundary case, and is described by connected hyperbola segments. The first and second cases have more complicated analytic forms, although the shape of the boundaries is very similar to hyperbolas. (Lemma V-4.7). In Figures 4, 5, and 6, opposite-edge boundaries are labeled f. In Figures 4 and 5 all three cases occur, while in Figure 6 the HCA is a virtual obstacle, that is, it appears to points outside it that it is an obstacle, so the only opposite-edge boundary it has is the third, or hyperbolic case.
HCA Corner-cutting boundaries occur when optimal paths cut into the HCA along an edge which is not part of the opposite-edge sequence. In fact, the analytic form of this boundary is just a variation of the second of the three types of opposite-edge boundaries discussed in the previous paragraph. Corner-cutting boundaries emanate from a vertex connecting a hidden and a visible edge when shortcutting occurs across those edges (for example, in Figure 5, labeled g). In the generalization of this case where the edges across which shortcutting occurs are separated by one or more edges, the corner-cutting boundary begins at the point at which the set of interior boundaries intersects the hidden edge (Lemma V-4.8).
The construction of interior-boundary trees is useful in finding exterior boundaries. There is exactly one opposite-edge or corner-cutting boundary associated with each interior tree of boundaries, and each visible HCA vertex is connected, either directly or via its interior boundary tree, to an opposite-edge or corner-cutting boundary. (Lemma V-4.11). When an interior boundary tree includes as a leaf node an interior hidden-edge-diverging-path boundary, the point at which the boundary intersects the HCA edge is connected with an exterior opposite-edge boundary. When an interior-boundary tree includes as a leaf node a point of intersection of an interior boundary and an HCA edge, but does not include an opposite point, for example, as happens three times along the hidden edge of the HCA in Figure 4, this point of intersection is connected with an exterior opposite-edge or corner-cutting boundary. When as happens to the rightmost vertex in Figure 5, a vertex is not connected with any interior boundary tree, corner shortcutting occurs and a corner-cutting boundary is connected with the corner vertex. Two HCA opposite-edge boundaries or corner-cutting boundaries may intersect each other or a shadow boundary, and if they do a third boundary begins at the point of intersection and lies away from the goal, as for obstacle opposite-edges.
An optimal path will travel into a high-cost HCA from outside it only across an edge which forms an angle greater than @ sin sup -1 (2 theta sub c )@ with another connected HCA edge [10]. If no hidden edge is associated with included angles of less than @2 theta sub c @ with connected visible edges and the cost ratio and dimensions of the HCA allow, it acts exactly as an obstacle with respect to all start-points outside the HCA. Such an HCA is called a virtual obstacle. The HCA shown in Figure 6 is a virtual obstacle. If all the opposite-edge and corner-cutting boundaries converge and become a single opposite-edge boundary away from the goal, the HCA becomes, for all points beyond the point of convergence, a virtual obstacle.
An HCA containing the goal point and with higher
cost than the surrounding terrain generates a set of exterior boundaries
similar to the high-cost exterior-goal case, while the interior boundaries
have a new character since it may be profitable
to move away from the goal point initially in order to travel along
an HCA edge in the exterior, lower-cost region.
Figure 7 illustrates the high-cost interior-goal case (see Theorem V-5).
We will define edges for this case with respect to
each of its vertices, so that an edge may be defined differently for
each of its endpoints. Define a visible edge with respect to
one of its vertices V as an edge for which the optimal path from V
cuts into the HCA interior at some point along the edge (either immediately
from V or along the edge interior). Define a hidden edge with
respect to V as an edge for which the optimal path from V starts along
the other edge incident to V, or for which no optimal path from any
point on the edge cuts directly into the HCA interior. Define an opposite
edge as an edge which is a hidden edge with respect to both its
vertices. There are four types of interior boundaries, which are line
segments and parabola segments. Each HCA vertex can generate a set
of boundaries. For each vertex V, if the optimal-path from that vertex
consists only of the goal point, i.e, if the optimal path from the
vertex goes directly to the goal, then there are no interior boundaries
associated with that vertex.
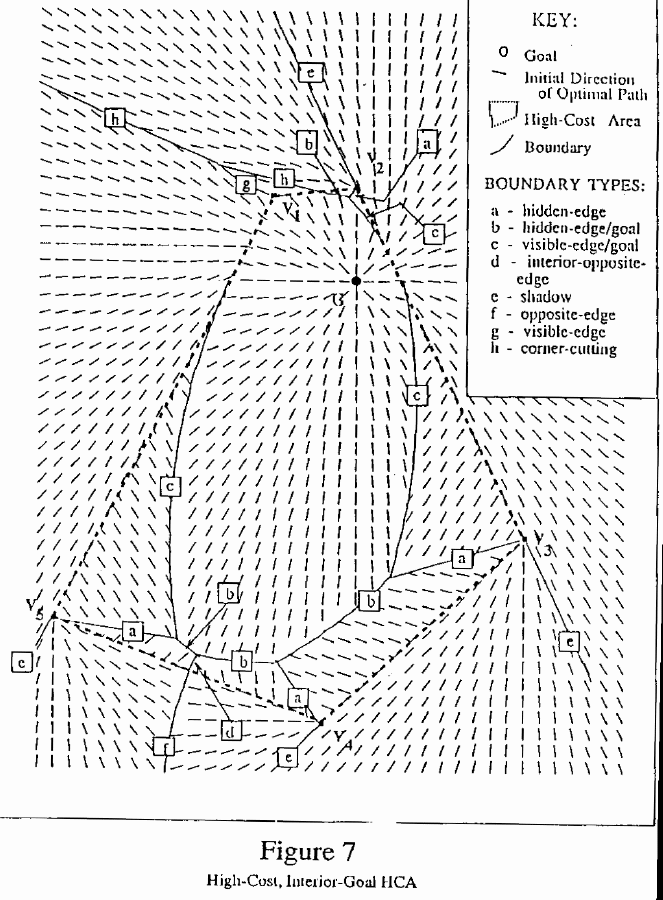
If on the other hand the optimal path from HCA vertex V travels initially along an HCA edge, call the edge along which the path travels initially @E sub 2 @, and call the other HCA edge incident upon V (along which the path does not travel) @E sub 1 @. In this case there will be a boundary associated with vertex V which is a line segment. This boundary starts at V and separates paths which cut over to edge @E sub 1 @ and go through V from those which cut over to edge @E sub 2 @, bypassing V. This is a hidden-edge boundary as defined for the exterior-goal case above. (In Figure 7, boundaries labeled a are hidden-edge boundaries. Also see the Appendix). In this case there will also be a parabolic boundary called a hidden-edge/goal boundary, which separates optimal paths which go directly to the goal from those which go initially away from the goal to edge @E sub 1 @ and from there through V and on around the HCA, cutting back in to the goal at another point on the HCA perimeter. This parabola is formed by considering the goal point as the focus, and constructing the directrix such that it is perpendicular to a line from V into the HCA exterior which forms an angle of @ pi over 2 + theta sub c @ with edge @E sub 1 @, and such that it is a distance d from V, where @d = { cost(OPL(V)) } over { c sub i }@. (See the boundaries in Figure 7 labeled b, and the Appendix.)
If in addition, the first turn point P on the optimal path from V is an interior point of edge @E sub 2 @, i.e., if the second leg of the optimal path from V cuts into the HCA to the goal, there will be a boundary called a visible-edge/goal boundary associated with V and edge @E sub 2 @ which separates paths that go directly to the goal from those which go initially back to @E sub 2 @ then travel along @E sub 2 @ to P, and then cut into the HCA at P to the goal. The visible-edge/goal boundary intersects the HCA edge at P. Again, the focus is the goal point, and then the directrix is perpendicular to a line from P into the HCA exterior which forms an angle with line segment PV of @ pi over 2 + theta sub c @, and which is distance d from P such that @d = { cost(OPL(P)) } over { c sub i } @. (See Figure 7, the boundaries labeled c, and Lemma V-5.3.)
The other type of interior boundary occurs when two adjacent vertices on a hidden edge have optimal paths which both lie initially on an HCA edge, but which go in opposite directions around the HCA (i.e., for which neither optimal path includes the other vertex). This is the same situation that occurs in the definition of an obstacle opposite-edge, and so such an edge is called an HCA opposite edge. However, there may be zero, one, or more opposite edges in this case. Each HCA opposite edge @V sub 12 @ generates an interior opposite-edge boundary, which separates paths which exit the HCA and go through vertex @V sub 1 @ from those which exit and go through vertex @V sub 2 @. (See Figure 7, the boundary labeled c, and Lemma V-5.4.)
The exterior boundaries in this case are quite similar to the high-cost exterior-goal HCA case. There are five types of exterior boundaries. HCA edges are trivial boundaries (Lemma V-5.5). Shadow boundaries are associated with each vertex V whose optimal path OPL(V) includes as its first path-vertex a point P on the HCA perimeter. The shadow boundary is constructed by extending a ray from V along line VP away from P. (See Figure 7, boundaries labeled e, and Lemma V-5.6.)
Opposite-edge boundaries emanate from each HCA opposite edge. An opposite-edge boundary begins at an opposite point with a hyperbola segment and extends outward from the HCA, being formed exactly as in the exterior-goal case. Since there may be more than one opposite edge, there may also be more than one opposite-edge boundary. (See Figure 7, boundaries labeled f and Lemma V-5.7.) Visible-edge boundaries separate paths which cross two edges en route to the goal. This type of boundary exists whenever an optimal path from an HCA vertex goes directly to the goal. The boundary starts at the vertex and lies outward, possibly terminating when it intersects the next kind of boundary. (See boundary labeled g in Figure 7, and Lemma V-5.8.) Corner-cutting boundaries emanate from points at which hidden-edge/goal boundaries from the interior intersect the HCA edge. They separate points whose optimal paths cross the edge from those which go around the edge vertex. These boundaries begin at the HCA edge and are concatenated with new curve segments at each point at which the earlier curve intersects a shadow boundary, as in the corner-cutting case above. (See boundaries labeled h in Figure 7, and Lemma V-5.9.)
Analysis of an HCA with lower cost than the surrounding
terrain, where the goal is in the HCA interior, shows a much simpler
set of boundaries (Theorem V-6). There will never be any boundaries
inside the HCA in this case, because there is no incentive for an
optimal path to move away from the goal to the high-cost, external
terrain, and there are no terrain-feature edges or vertices between
any point in the HCA and the goal, since our HCA's are assumed convex.
(See Lemma V-6.1) External boundaries will occur in pairs,
forming a wedge emanating from each vertex of the HCA. Call this type of
boundary a vertex/edge-crossing boundary (see Lemma V-6.2). Figure 8
shows a low-cost HCA with interior goal, and the boundaries it induces
on the plane.
The final case, where the cost inside the HCA is lower than the
surrounding terrain and the goal is outside the HCA, bears some
similarities to the low-cost, interior-goal case and some to the
high-cost, interior-goal case. Then parabolic and similar boundaries
occur outside the HCA, and the wedges which occur in the low-cost,
interior-goal case are present in this case as well. Only one type of
boundary occurs in the HCA interior, and seven types occur in the HCA
exterior (Theorem V-7). Figure 9 illustrates a typical low-cost,
exterior-goal HCA.
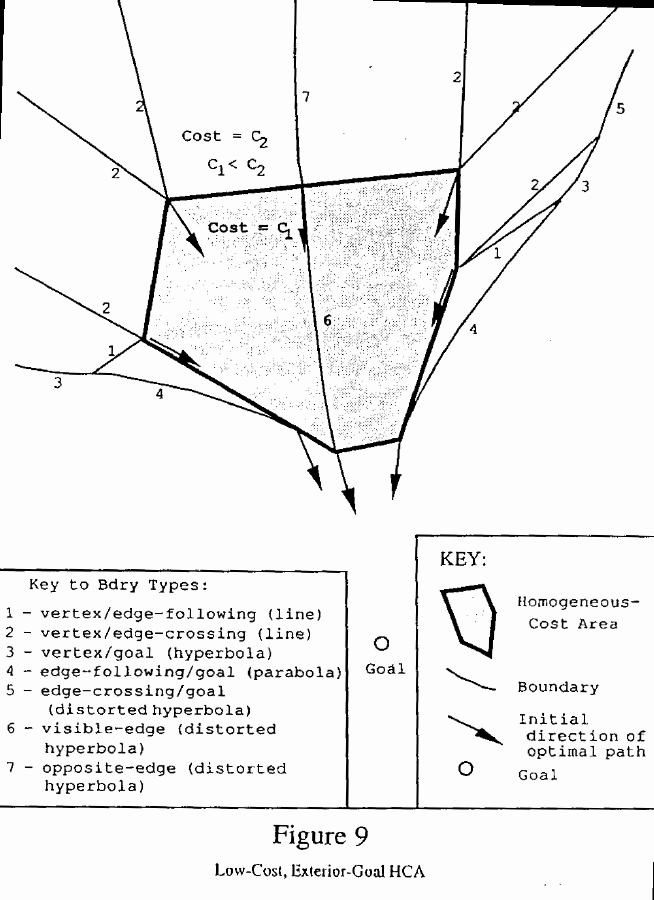
In the exterior, in addition to the trivial edge-boundaries (Lemma V-7.1), boundaries can be constructed by considering the behavior of the optimal path from each of the HCA vertices. For each vertex V of the HCA, let @E sub 1 @ and @E sub 2@ be the edges incident upon V, while @V sub 1 @ and @V sub 2 @ are the vertices such that @VV sub 1 = E sub 1 @ and @VV sub 2 = E sub 2 @. Additionally, let vertex @V sub 1 @ be closer to the goal than vertex @V sub 2 @, i.e., the cost of the optimal path from @V sub 1 @ be less than the cost of the optimal path from @V sub 2 @.
If the optimal path from V goes initially along HCA edge @E sub 1 @, (note that it will not go along @E sub 2 @ because of the naming convention above), the paths treat the edge like a road. Let P be the first point on the optimal path from V, which will be the point at which the path exits the HCA interior toward the goal. A vertex/edge-following boundary and a vertex/ edge-crossing boundary are associated with the paths from V with respect to edges @E sub 1 @ and @E sub 2 @ respectively. The vertex/edge-crossing boundary is a ray with vertex V lying in the HCA exterior such that the ray and the first leg of the optimal path from V form a Snell's-Law crossing of HCA edge @E sub 2 @ (see Lemma V-7.2). This type of boundary separates paths which go to vertex V and then along edge @E sub 1 @ from those that go directly to @E sub 1 @ and follow along it. The vertex/edge-following boundary is a special case of the vertex/edge-crossing boundary where the Snell's-Law angle of the ray with edge @E sub 1 @ is the critical angle @ theta sub c @ (see Lemma V-7.3). These boundaries are labeled 1 in Figure 9. The vertex/edge-crossing boundary separates paths which go to a vertex V and then cut into the HCA interior from those that cross edge @E sub 1 @ into the interior. In Figure 9, these boundaries are labeled 2.
Also occurring is an edge-following/goal boundary which is a parabola with the goal point as focus and directrix perpendicular to a line from P at an angle @ pi over 2 + theta sub c @, lying a distance d away from P where d is the cost of an optimal path from P. This type of boundary separates paths which go to edge @E sub 1 @ and follow the edge from those which go directly to the goal (see Lemma V-7.4). Figure 9 has these type of boundaries labeled 4. Additionally, a vertex/goal boundary occurs beginning at the point at which the edge-following/goal boundary intersects the vertex/edge-following boundary, and is a hyperbola segment with V and G being the foci, and the hyperbolic constant being the cost of the optimal path from V (see Lemma V-7.5). Figure 9 labels this type of boundary 3. This boundary may continue indefinitely, or it may intersect the vertex/edge-crossing boundary emanating from V. If these two intersect, both terminate at the point of intersection and a third boundary discussed below begins.
For each HCA vertex V for which the optimal path from V goes initially into the HCA interior, a pair of linear vertex/edge-crossing boundaries will occur, just as in the interior-goal, low-cost case. These boundaries separate points whose optimal paths enter the HCA through a hidden vertex from those which enter through a hidden edge. Each boundary is constructed by extending a ray from V into the HCA exterior such that the ray and the first leg of the optimal path from V form a Snell's-Law crossing of @E sub 1 @ and @E sub 2 @ respectively. If in addition the vertex/goal boundary associated with vertex @V sub 1 @ intersects the vertex/edge-crossing boundary emanating from @V sub 1 @ associated with edge @E sub 1 @, a third boundary begins. If the first point P along the optimal path from V is an HCA vertex, the boundary will be an edge-following/goal boundary, a parabola, as discussed above. If P is an interior point of an HCA edge, the boundary will a more general type of curve similar in shape to a parabola, called an edge-crossing/goal boundary (see Lemma V-7.6) In Figure 8, these type of boundaries are labeled 5. A vertex/goal boundary also occurs, beginning at the point at which the edge-crossing/goal boundary intersects the vertex/edge-crossing (or edge-following) boundary associated with edge @E sub 1 @. Whenever an interior boundary (see below) intersects a hidden edge of the HCA, an exterior boundary begins, called an opposite-edge boundary (see Lemma V-7.8 and Figure 8 boundary labeled 7). Opposite-edge boundaries separate paths which cross an edge into the HCA interior and then go across the HCA to exit across a second, visible edge, from those which cross the same first edge into the HCA but exit across a third, visible edge. Just as in the high-cost, exterior-goal case, these boundaries may intersect and new opposite-edge boundaries begin, but in this case they are of only one type and separate paths which cross one pair of edges from those which cross another pair.
There is only one type of boundary in the interior of a low-cost, exterior-goal HCA. It begins at a visible vertex which is not directly connected to any other boundaries, and separates points whose optimal paths cross one visible edge incident to the vertex from those which cross the other visible edge. Because of its similar boundary type in the high-cost exterior-goal case, it is called a visible-edge boundary (see Lemma V-7.7 and the boundary labeled 6 in Figure 9). Just as in that case, the interior boundaries may intersect and generate new boundaries, which are also visible-edge boundaries. Whenever a visible-edge boundary intersects a hidden edge, the visible-edge boundary terminates and an opposite-edge boundary begins in the HCA exterior. Both the visible-edge boundary and the opposite-edge boundary types are similar in shape to hyperbola segments, although their algebraic form is not expressible in closed form. These boundaries typically have very little curvature.
The cost of optimal paths from each start point in the plane is a function of the location of the start point. In other words, there is a cost function of X and Y which characterizes the entire map. Consider the region around the goal, for which the goal is the region root. Cost is proportional to distance from the goal, in the absence of intervening terrain, so iso-cost contours form circles about the goal. This cost function is an inverted cone with vertex at the goal-point, or the upper half of a cone as defined in classical geometry. In any homogeneous-behavior region with a point as its root, there will be some additional cost of the optimal path from the root to the goal. For each region whose root is a single point then, the cost function in the region will be conical with respect to a vertical axis through the point. The vertex of the cone representing the cost function will be shifted upward on the cost axis by the amount of the cost of an optimal path from the root.
Another type of region root is an edge along which, on the lower-cost side, paths travel en route to the goal. The path from a point whose optimal path reaches the edge to travel along it does so at the critical angle @ theta sub c = sin sup -1 (C sub r / C sub b )@, where @C sub r @ is the cost of traveling a unit distance along the edge and @C sub b @ is the cost of traveling a unit distance in background terrain. Therefore, the cost of traveling from the point of entrance onto the edge @P sub E @ to the point of exit from the road @P sub X @ is @C sub r | P sub E P sub X | = C sub b sin theta sub c | P sub E P sub X | @.
The cost of traveling from point S to the edge and along it to the point of exit @P sub X @ is then @ | SP sub E |C sub b + |P sub E P sub X |C sub b sin theta sub c = C sub b ( | SP sub E | + |P sub E V sub X | sin theta sub c ) @. Consider a right triangle with hypotenuse @P sub E P sub X @, with one leg a continuation of @SP sub E @ to the other side of the edge from S to point Q. Now @|P sub E Q| = |P sub E P sub X |sin theta sub b @, so the cost of traveling from S to @P sub E @ and along the edge to @P sub X @ is @C sub b (|SP sub E | + |P sub E Q|) = C sub b |SQ| @ since @S, P sub E @, and @Q@ are colinear. Thus, the cost from any point S to move to an edge and travel along it to some point @P sub X @ is proportional to the distance from S to a line at angle @ theta sub c @ with the edge and passing through @P sub X @. But by this description, S describes a plane which intersects line @QP sub X @ lying in the plane of the map, such that the slope of the plane in the gradient direction is @C sub b |SQ|/|SQ| = C sub b @. So the cost function associated with a length-wise-traveled edge is a plane.
A third type of region root is an edge which paths cross, obeying Snell's Law as they do so. As each path crosses the edge, it enters a region where the cost function becomes proportionally greater or less than before. But each edge which is crossed according to Snell's Law performs a transformation on the current cost function, or intuitively speaking, distorts the cost function. The cost function associated with a Snell's-Law edge is therefore a distortion of the cost function associated with the parent of the edge in the optimal-path tree. Thus there are two cost functions associated with Snell's-Law edges, one where the cone of a point-type root is transformed by the edge resulting in a distorted cone, and one where the plane of a edge-type root is transformed by the Snell's-Law edge, resulting in a plane. For regions with conical cost functions, paths which crossed into it from a region with a lower cost would have a cost function which was a flattened "cone". Paths crossing into it from a region with a higher cost would have a cost function which was a "cone" with greater curvature. For regions with planar cost functions, higher-cost adjacent regions would have a more sloped cost function, while lower-cost adjacent regions would have a less sloped cost function.
There are any number of "higher-order" cost functions associated with Snell's-Law edges ending in a point. For example, paths could cross three edges enroute to a point. So it does not appear to be possible to derive a finite number of analytic characterizations of cost functions for all varieties of Snell's-Law edges. Note, however, that although a cost function may be transformed by any number of Snell's-Law edges, it has its basis in either a point or a linearly-traversed edge root, so there are really only two general classifications of Snell's-Law cost functions, those for n crossings rooted in a point, and those for n crossings rooted in a linearly-traversed edge. Once a sequence of region roots leads back to a point or a traversed edge, a fixed cost is associated with the point or the goal end of the edge, which is the cost from that point to the goal, and so no other previous information about cost functions remains relevant.
Since these are the only types of region roots which occur in the terrain defined for this research, there are only three general types of cost functions: cones, planes, and various orders of distorted cones, depending respectively on whether the region has a point as its root, a linearly-traversed-edge or one or more Snell's-Law edges ending in a linearly-traversed edge as its root, or finally a Snell's-Law edge as its root leading to one or more Snell's-Law edges and a point.
The occurrence of many of the simpler types of boundaries can now be explained in terms of the cost functions of the region roots for regions which the boundary separates. Since at a boundary between two regions, the cost function for both regions applies, it must be that the boundary is the projection on the XY plane of the intersection of the two cost functions. The intersection of two cones with parallel axes is, according to basic analytic geometry, a hyperbola, and so it becomes clear why the boundary between two regions with points as roots is always a hyperbola.
The intersection of two planes is a line, so the boundary between regions which both have linearly-traversed edges as roots is a line segment. For example, the hidden-edge merging-path boundary of a high-cost, external-goal HCA. The boundary between a region whose root is a point and a region whose root is an cost-region edge was shown in Section 2.2 to be a parabola. Since the slope of the plane which is the cost function of the edge's region was shown above to be the cost rate of the background, and the slope of the cone is also the cost rate of the background, we have the condition which specifies in intersecting a plane with a cone that the intersection is a parabola.
The more complicated boundaries involving one or more Snell's-Law edges ending in a point also are consistent with this view, although the mathematics involved in computing the intersections of generalized shapes is complex. Boundaries involving Snell's-Law edges ending in a linearly-traversed edge are of the same types as those involving single linearly-traversed edges. Since there are three general types of cost functions, and each boundary can be described as the intersection of two cost functions, there are six non-redundant ways that two cost functions may intersect, as in Table 5. Each entry in the last row and the last column depends on the number of edges crossed by the region root, and will be different for different numbers of edges. For some cases, a boundary listed as a parabola, hyperbola, or distorted parabola or hyperbola will degenerate to a straight line.
The algorithm to compute the planar partition for high-cost area with an external goal is called hca-opm-high-ext (see Table 1). The equations for each boundary can be found in the Appendix. Each vertex of such a HCA is associated with an internal boundary, whose character depends on whether the edges incident to the vertex are visible or hidden (and for vertices on two hidden edges, on whether the vertices nearest the goal for each edge have optimal paths which go in the same, or different directions around the HCA, called merging or diverging paths respectively). These boundaries are computed first, and then procedure pair-and-merge-bdrys constructs a network (or networks) of interior boundaries which is connected to the initially-computed boundaries. This procedure pairs boundaries which intersect, and then plots a new boundary which has an endpoint at the point of intersection of the paired boundaries. It continues pairing boundaries and plotting new ones until all the boundaries are joined together on both ends or intersect an edge of the HCA. Note that deciding which adjacent boundaries should be paired together is not simple, and it may take several iterations for the procedure to settle on a correct configuration.
The interior boundaries are then joined into trees, and since each interior boundary tree intersects an opposite edge exactly once, this can serve to begin generation of the external opposite-edge boundaries. There can be several HCA opposite edges and opposite-edge boundaries. Corner-cutting boundaries are indicated when an interior boundary associated with a vertex actually begins, not at the vertex, but somewhere along the boundary. The algorithm next checks for this situation, which can only happen with respect to a vertex joining a hidden and a visible edge. This type of vertex is also a good place to begin generating shadow boundaries. Finally, procedure pair-and-merge-bdrys is again used, this time with the exterior shadow and opposite-edge boundaries.
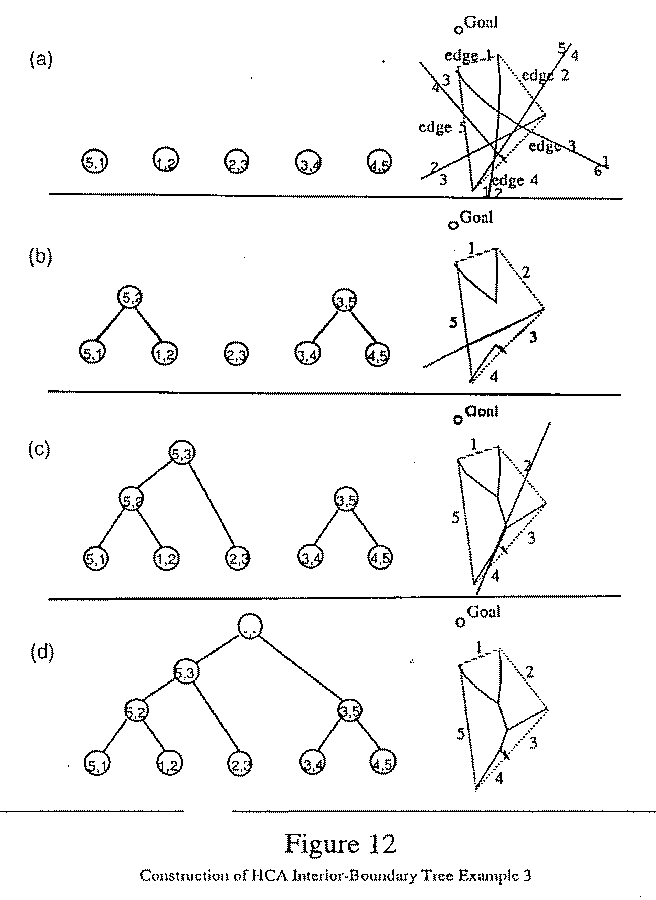
Figures 10, 11, and 12 illustrate the state of procedure
pair-and-merge-bdrys at various intermediate stages in its execution
for the example HCAs of Figures 4, 5, and 6 respectively. Edges
of the HCAs are numbered, and boundaries are labeled "i,j", where
i and j represent the edges crossed by paths on either side of the
boundary. Boundaries which are paired with another boundary at each
stage are noted by an asterisk. Boundaries which are stored in the
data structure PairedBdrySet are noted in the Figures as dark lines.
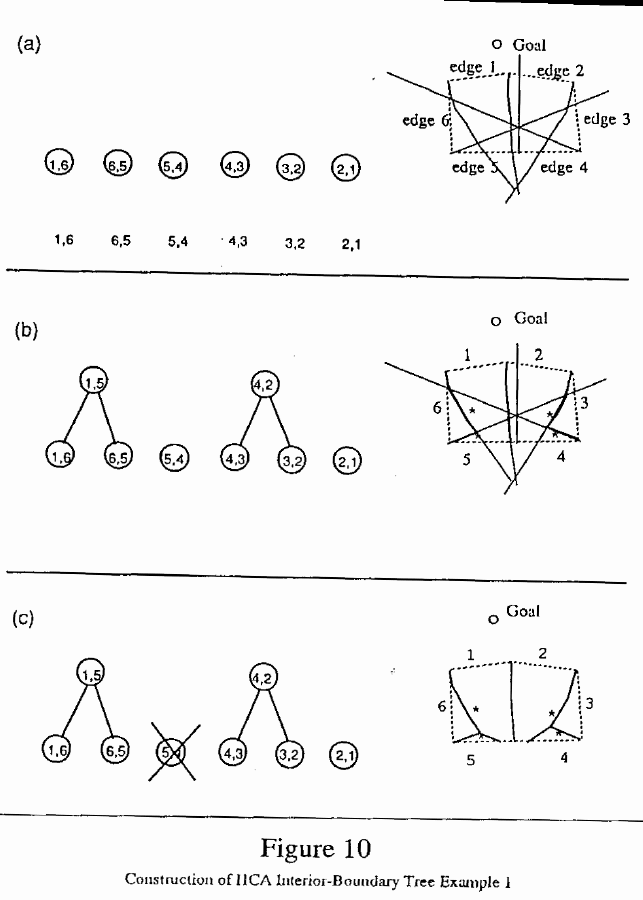
Figures 10a, 11a, and 12a show the interior boundaries associated with
each terrain-feature vertex at the beginning of the algorithm (beginning
at the vertex or associated short-cutting point, extending indefinitely
into the interior and then beyond. The current set of interior-boundary
trees is also shown, with each node labeled by the boundary it represents.
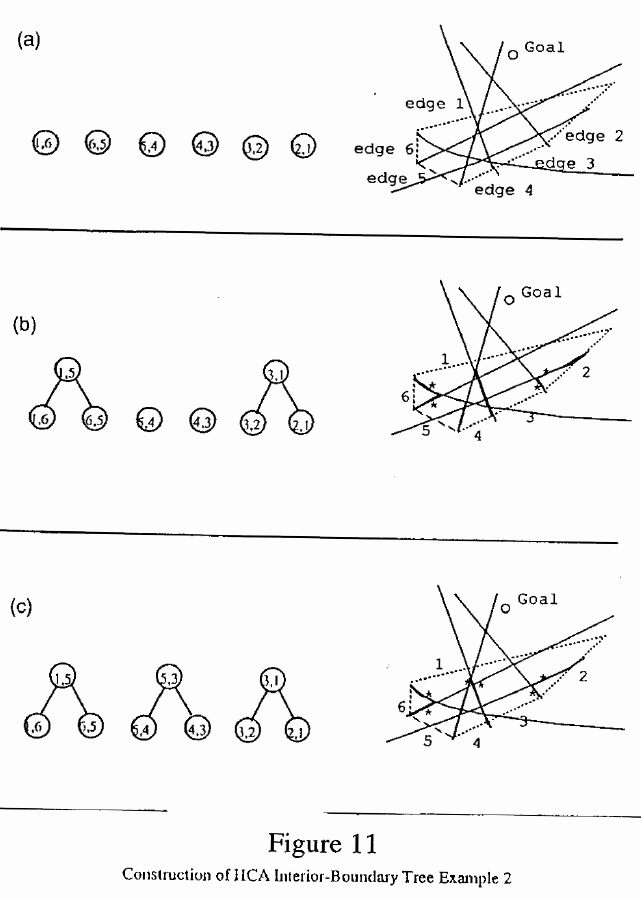
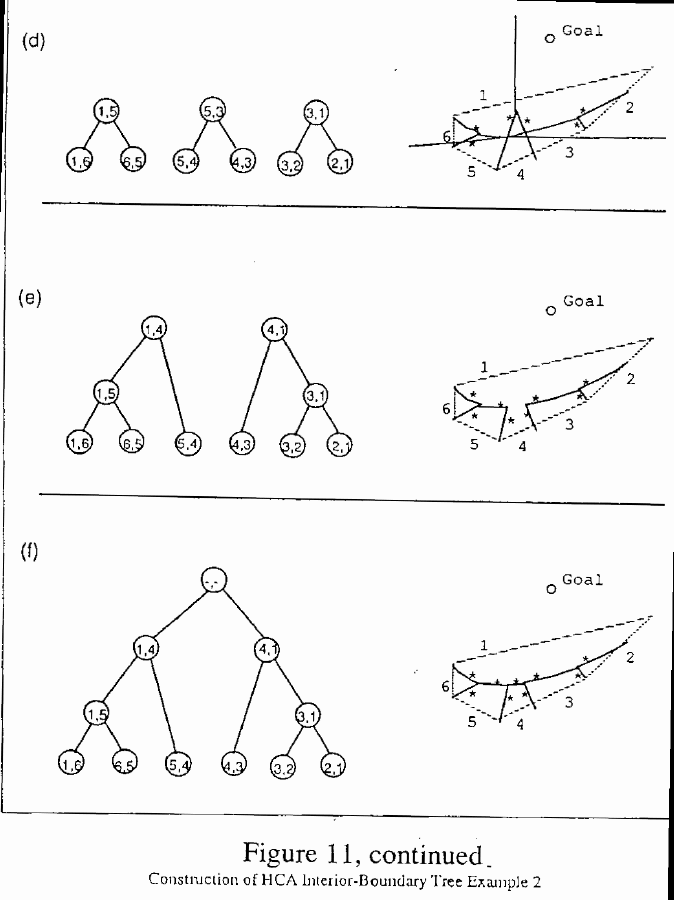
Consider, for example, Figure 11. Figure 11b shows the state of PairedBdrySet with respect to the HCA after the first pass through the inner loop ("while PairedBdrySet is changing"), where each boundary "i,j" in the initial set of boundaries is intersected with the two adjacent boundaries, and the shortest version of "i,j" is retained in PairedBdrySet. Those boundaries which pair up with an adjacent boundary are marked with "*". In Figure 11b, "1,6" pairs with "5,6" and "1,2" pairs with "2,3". "4,5" and "3,4" were not marked, and so are going to be replaced in PairedBdrySet by the full versions of their respective boundaries at the start of the next pass through the inner loop. After the second pass through the inner loop, all boundaries are marked as in Figure 11c, so on the next iteration no changes to PairedBdrySet will be made, so the "while changing" condition will fail, ending the inner loop.
As the outer loop ("while BdrySet is changing") finishes its first pass, new boundaries are generated from each intersection point of paired boundaries, and these boundaries are placed, unmarked, into PairedBdrySet, which replaces BdrySet. This situation is reflected in Figure 11d. Figure 11e reflects the state of PairedBdrySet after the outer loop has started its second pass, and the inner loop has run until it stabilizes again. Note that some boundaries which were paired after pass one, i.e., "4,5" and "3,4", are in fact intersected by second-level boundaries instead, and so the truncated versions of the boundaries need to be retracted from PairedBdrySet and the full versions put back into PairedBdrySet for further interaction with second-level boundaries. This illustrates why such this procedure is complicated, because we are not able to tell with a single pass which boundaries will be paired. Boundary "1,4" is now propagated from both directions from the intersection points of "4,5" and "1,5" as well as "1,3" and "3,4". It is truncated at both ends and paired with itself, after which the configuration is stable. Thus BdrySet will not change further, so the outer loop will halt with BdrySet as illustrated in Figure 11f. At each stage, the interior-boundary trees are built up until, in Figure 11f, a single tree results.
In algorithm hca-opm-high-ext, it is assumed initially that there is an opposite point, i.e., a point on the hidden side of the HCA where two optimal paths go in opposite directions around the HCA. Further, this assumed opposite point is initially considered a vertex for the purposes of the algorithm. Figure 10 shows a situation where the algorithm leads to the conclusion that the opposite point does not exist after all, and so there is no interior boundary incident to it, because there is shortcutting of paths from the outside of the HCA across the HCA to the goal. The figure also shows a situation where there is more than one interior-boundary tree. There is one exterior opposite-edge boundary incident upon an HCA edge associated with each interior-boundary tree. It has one endpoint at the point at which a boundary of the tree intersects an opposite edge.
A much different algorithm is needed to construct boundaries for the case of a high-cost HCA with an interior goal point (see Figure 7). The existence of interior boundaries are more predictable without the need for the iterative checking as in the high-cost, exterior-goal HCA case. It is still necessary, however, to check the intersections of various boundaries and truncate them appropriately, and insert portions of edges into the optimal-path tree, which is done at the algorithm's conclusion. (See Table 2.)
The algorithm proceeds by looking at each HCA vertex in turn, and determining by observing its optimal path whether it is a hidden or a visible vertex. If it is a hidden vertex, the path from the vertex will travel along an edge of the HCA before cutting into the interior, while if it is a visible vertex, the path will go directly to the goal. If it is hidden, several interior boundaries and one exterior shadow boundary are generated, as well as possibly an opposite-edge boundary. If it is visible, only one exterior boundary, a visible-edge boundary, is generated.
It is necessary to insert portions of edges into the optimal-path tree according to the traversal characteristics of optimal paths across or along them. For example, it is possible for a portion of an edge from one vertex to act like a road, where paths leave the HCA interior to travel along the lower-cost edge, and then cut back in to the HCA when nearer to the goal. Thus the first portion of the edge would be the root of a homogeneous-behavior region characterized by paths crossing from the interior to the exterior and traveling along the edge, and the next portion of the edge would be the root of another region characterized by paths crossing from exterior to interior. All this information is not available when processing each individual vertex, however, so edges which may become region roots are stored temporarily, and at each step when information is gained which could rule out portions of edges as roots, that information is stored as a "mask", which can mask out portions of edges. At the conclusion of the algorithm, these edges and masks are processed to determine exactly which portions of edges belong as region roots in the optimal-path tree. Also done at the conclusion of the algorithm is the intersecting of opposite-edge and shadow boundaries and plotting of new boundaries in the HCA exterior, much like in the interior of a high-cost, exterior-goal HCA.
The exterior-goal-low-cost-region algorithm shown in Table 3 looks at each HCA vertex in turn, basing its logic on the initial direction of the optimal path from the vertex being examined (see Figure 8). If the optimal path from a vertex goes into the HCA interior, two rays, or vertex/edge-crossing boundaries, are constructed forming a wedge outward from the vertex and away from the goal. If the optimal path goes along an edge of the HCA, one of the above boundaries, the one closer to the direction of travel of the optimal path, is instead a vertex/edge-following boundary, and in addition a parabolic, or vertex/goal boundary is constructed. The third possibility is that the optimal path goes directly into the HCA exterior, i.e., toward the goal. If so, more boundaries may or may not be generated. If a portion of each edge adjacent to the vertex is visible to the goal, i.e., if for both edges there are paths starting at some points on the edges which go directly into the HCA exterior, then a visible-edge boundary will emanate from the vertex into the HCA interior.
With the above boundaries generated, two tasks remain. First, each parabolic, or edge-following/goal boundary must be followed away from the goal to see if it intersects the next ray boundary. If so, a hyperbolic, or vertex/goal boundary will begin, with one focus at the vertex. This hyperbola must then be followed in turn. If it intersects a ray boundary, a "distorted-parabolic", or edge-crossing/goal boundary will begin. As we continue to follow this sequence of boundaries, hyperbolas and distorted-parabolas occur alternately until no intersection with a ray is found. Note that this algorithm generates each parabolic and distorted-parabolic boundary in the initial phase, and then generates hyperbolas as needed in procedure add-hyp-bdrys-for-low-ext-hca below, which in addition truncates each boundary as necessary.
Although this type of HCA has interior boundaries, which one might suppose would need to be paired and merged as with the high-cost, exterior-goal case, in fact it is not necessary to do this. The reason is that such boundaries are all of the visible-edge type, and because the HCA interior is of lower cost than the surrounding terrain, these boundaries will never intersect. Intuitively in the high-cost exterior-goal case, a path travels to an edge further away in straight-line distance in order to take advantage of the lower external cost outside that edge, and at that point, two boundaries would intersect and a third emerge. Here, however, the path is already in the least costly terrain possible, and so further paths will continue to follow the same paths as those closer to the goal. For each visible-edge boundary, a point of intersection is plotted with the far edge of the HCA, and an opposite-edge boundary is generated, which is really just a continuation of the visible-edge boundary after crossing another edge.
Procedure construct-low-ext-hca-bdry performs the low-level function of generating each boundary for the low-cost, exterior-goal HCA as needed. For boundaries whose forms are general curves, the reader is referred to the Appendices.
Algorithm hca-opm-low-int is the simplest of the four HCA algorithms, in keeping with the simple nature of the regions and boundaries associated with this type of HCA (see Figure 9 and Table 4). Since a low-cost, interior-goal HCA generates only one wedge of two rays at each vertex, and these rays are guaranteed by the orientation of the HCA edges not to interact, the corresponding algorithm can do its work in one pass through the list of vertices.
Although the investigation into the problem of creating optimal-path maps for multiple HCAs is not complete in all its details, we propose the following high-level description of such an algorithm (see Table 5). Methods for constructing Voronoi diagrams [7] provide a model for approaches to the construction of an optimal-path map for multiple terrain features. Voronoi diagram methods use a divide-and-conquer approach, in which the points in the plane are divided into two roughly equal sets, the Voronoi diagrams of the two sets computed recursively, and the two Voronoi diagrams merged to produce the final one. The first key question is how to divide the points in the plane. The answer is that in order to support the merge phase, the plane is partitioned into two half-planes by a line (by convention, a vertical line) which equally divides the set of points in the plane. The other key question is whether the two intermediate Voronoi diagrams can be merged. Standard generalized-Voronoi-diagram construction algorithms provide an affirmative answer to this question, depending on the fact that the boundary between any two Voronoi regions in binary terrain (i.e., obstacles on a homogeneous-cost background) is a straight line segment or a hyperbola segment [5].
The analogous questions with respect to optimal-path map construction are whether terrain features can be divided in the same way as points, and how two optimal-path maps with the same goal can be merged into a single, combined OPM. An encouraging aspect of this problem is that when constructing OPM's for single terrain features, we rely on the optimal paths from only the terrain-feature vertices, which are computed by standard point-to-point path planners and take all the features of a map into account. Thus the optimal paths from any vertex will remain the same regardless of which terrain features are incorporated into the OPM. Another important aspect of this problem is the unifying perspective with regard to regions and boundaries proposed earlier. Since there are only three types of non-degenerate region roots, i.e., points, edges traversed length-wise, and edges traversed cross-wise (according to Snell's Law), it should be possible at the intersection of any two general boundaries to generate a new boundary by considering the six types of boundaries between regions of three possible types of roots.
To divide such decomposable terrain features into two approximately equal sets whose resulting OPM's can be merged is not difficult. In fact, it appears that any partition is feasible as long as it does not split a terrain feature, but some will be much more efficient than others. The advantage of a divide-and-conquer algorithm is its logarithmic performance in the recursive stage if it is guaranteed that divisions are approximately equal-sized, so any partitioning procedure should have this property. Also, it should not take an excessive amount of time to partition, since this step will play an important part in the overall time complexity. And thirdly, since the merging step will depend on checking for intersections between all boundaries of one sub-OPM and all boundaries of the other, it would be very useful if it were not necessary actually to check most of these boundaries. This would be the case if at each step in the recursion, the two OPM's represented terrain which did not, loosely speaking, "interleave". For such OPM's, boundaries which lay wholly within the interior of the two planar partitions would not have to be checked for intersection.
The merge step depends on the fact that any two boundaries, when they intersect, represent the meeting point of three regions, one of which is common to both boundaries. A new boundary will emanate from the point of intersection which separates the two regions which the original boundaries did not have in common. Rather than attempt to study all the special cases of possible region intersections among boundaries present in the nine algorithms thus far presented, it is preferable to use the unifying approach to boundary generation which considers the two types of region roots involved and selects from the limited number of boundary types to find the new boundary. However, since there are infinitely many possible types of Snell's-Law edges based on the number of edge-crossings between the edge and the goal, an approximate solution is proposed. Since boundaries between Snell's-Law edges are similar to hyperbolas, it is proposed that for all except the varieties already derived in the Appendix, hyperbolas be used as approximations to the exact curves.
When a new boundary has been generated because of the intersection of two boundaries from different sets, the effects may propagate into both partial OPM's. This will be, in the worst case, a very expensive operation, because unlike Voronoi diagram construction, the boundaries between regions are not simple lines, and the effects are not guaranteed to be local. Each boundary which is truncated by the new boundary must be followed to its end (before it was truncated), and if it intersected other boundaries, these in turn must be reconsidered with respect to the new boundary.
Algorithm VI-9 describes this method of constructing an optimal-path map for input maps containing any number and kind of HCAs. At each level of recursion, the algorithm divides the terrain into two roughly equal sets, based on a calculation of the median leftmost vertex. At the lowest level, that of a single terrain feature, the algorithm calls on Algorithms VI-1 through VI-8 to construct an OPM for the feature. At higher levels, OPM's are merged by procedure merge-opms.
Each boundary whose analytical form does not have a closed-form solution is represented by a piecewise-linear approximation. These boundaries are plotted parametrically, iteratively setting one parameter and solving for the other. Fortunately for the precision of the algorithm, most boundaries had very little curvature in experiments, too small to be seen on an 8.5 by 11 sheet of paper. What error does occur will cause start points which are close to a boundary to be placed in an incorrect region. The cost error will be no greater than the cost-rate in the region times the maximum distance of the piecewise-linear approximation from the actual curve, a generally very small number.
The algorithm of [4] is @O ( n sup 7 L ) @ in time complexity in the worst case, @L@ an accuracy parameter, and the algorithm of [10] is @O ( n sup 2 )@ in the average case, @n@ the number of terrain vertices. We ignore this phase in the subsequent discussion.
We first consider the high-cost-exterior-goal HCA OPM algorithm. For a HCA with n vertices there are at most n shadow boundaries, which can be constructed in O(n) time by a depth-first traversal of the the optimal-path tree, generating a shadow boundary for each node in the tree. Each hyperbola segment which is part of the opposite edge can be constructed in constant time, and there are at most n-2 intersections of the opposite-edge boundary with shadow boundaries. Thus the opposite-edge boundary can be constructed in O(n) time, so the entire OPM can be constructed in O(n) time. Each shadow boundary and each hyperbola segment of the opposite-edge boundary can be represented in O(constant) space. Since the optimal-path tree can be stored in O(n) space, and assuming constant accuracy, the representation of the entire OPM is O(n) space.
However, the interior boundaries can be more time-consuming. In the worst case, each pair of these boundaries intersects and a third boundary begins at the intersection point, giving n/2 new boundaries, and each pair of new boundaries intersects and another begins, for n/4 new boundaries at the third level, and so on until a final boundary occurs which connects all the others. Then there are n+n/2+n/4+n/8+...+1 boundaries. There are in the limit n/(1-1/2) = 2n boundaries. Procedure pair-and-merge-bdrys takes at worst n-2 passes through the inner ("while PairedBdrySet is changing") loop, which itself processes n boundaries. The outer loop, which checks for intersections by newly propagated boundaries with already-paired boundaries, could also take O(n) passes in the worst case. Thus procedure pair-and-merge-bdrys, and thus the whole algorithm, is @O ( n sup 3 )@. The space complexity is O(n) because at most 2n interior boundaries, n-2 shadow boundaries, and n-2 portions of opposite-edge boundaries exist.
As for the high-cost-interior-goal-HCA-OPM algorithm, for each vertex at most one exterior and four interior boundaries are generated, as well as additional boundaries for each pair of visible edges and each interior opposite-edge boundary. Both the exterior visible-edge boundaries and the exterior opposite-edge boundaries display the same behavior as obstacle opposite-edge boundaries, so that all of them together have no more than O(n) segments. The only iterative loop in the algorithm is the outer one which processes each of the n vertices, so the overall worst-case time complexity is O(n), as is the space complexity.
As for the low-cost-exterior-goal-HCA-OPM algorithm, it generates at most four boundaries per HCA vertex. Although there are interior boundaries similar to the high-cost, exterior-goal case, here they are never mutually intersecting. Thus the entire algorithm has time complexity O(n). The space complexity is also O(n).
As for the low-cost-interior-goal-HCA-OPM algorithm, there are exactly two linear boundaries emanating from each HCA vertex. Thus the time and space complexity is O(n).
This algorithm spends O(n) time dividing the map at each stage of size n, by standard median-finding algorithms from computational geometry. Let the time complexity of the algorithm itself be expressed as T(n). Then the recursive application of the algorithm to both halves of the map will take 2T(n/2) time. Thus the dividing, recursion, and merging will take T(n) = O(n) + 2T(n/2) + O(f(n)), where f(n) is the time complexity of the merge step.
The procedure merge-opms is very similar to procedure pair-and-merge-bdrys associated with the algorithm for high-cost, exterior-goal HCA OPM's, which joined the interior boundaries and propagated new ones as needed. It is subject to the same possibility that multiple levels of newly-propagated boundaries may occur, and has the added complexity that for each boundary truncated in one of the subordinate OPM's, the procedure intersect-and-merge must be performed to reconstruct any other boundaries which previously intersected the truncated boundary but no longer do so. By the same reasoning as above, even assuming that procedure intersect-and-merge has O(constant) worst-case time complexity, procedure merge-opms operates in @O ( n sup 3 )@ time. In fact, procedure intersect-and-merge operates in O(n) time in the worst case, because there are at most O(n) boundaries which a boundary can possibly intersect. Thus, procedure merge-opms has worst-case time complexity @O ( n sup 4 )@. We note also that the base case of the recursion requires the solution of a single-terrain-feature algorithm, which may have as much as @O ( n sup 3 )@ time complexity. Thus the worst-case time complexity of the entire algorithm may be stated as T(n) less than @O ( n) + 2 T ( n / 2 ) + O ( n sup 4 )@. By further analysis [1], it can be shown the the whole algorithm is @O ( n sup 4 )@.
The high-cost, exterior-goal case, was implemented as a proof-of-concept program. The high-cost, exterior-goal HCA was chosen because it was the most complex of the seven cases and incorporated most of the types of boundaries. The implementation was not intended to be particularly efficient, but was primarily designed to corroborate the shapes of various boundaries when compared with multiple runs of a point-to-point weighted-region path-planning implementation by Richbourg [10]. OPMs of fairly simple complexity such as the above three Figures took four to six minutes apiece to construct, not counting the OPM construction. This implementation was done in C-Prolog on a VAX 11/785 running under BSD 4.3 Unix.
[1] Alexander, R. S., "Construction of Optimal-Path Maps for Homogeneous-Cost-Region Path-Planning Problems", Ph.D. thesis, U.S. Naval Postgraduate School, Department of Computer Science, September 1989.
[2] Lee, D. T. and Preparata, F. P., "Euclidean Shortest Paths in the Presence of Rectilinear Barriers", Networks, 14, pp. 393-410, 1984.
[3] Mitchell, J. S. B., "An Algorithmic Approach to Some Problems in Terrain Navigation", Artificial Intelligence, Vol. 37, 1988, pp. 171-201.
[4] Mitchell, J. S. B., and Papadimitriou, C. H., "The Weighted Region Problem", to appear in Journal of the ACM, 1990.
[5] Mitchell, J. S. B., "A New Algorithm for Shortest Paths Among Obstacles in the Plane", to appear in Journal of the ACM, 1990.
[6] Payton, D. W., "Internalized Plans: A Representation for Action Resources", presented at the Workshop on Representation and Learning in an Autonomous Agent, Faro, Portugal, 1988.
[7] Preparata, F. P., and Shamos, M. I., Computational Geometry, An Introduction, Springer-Verlag, 1988.
[8] Reif, J. H., and Storer, J. A., "Shortest Paths in the Plane with Polyhedral Obstacles", Technical Report CS-85-121, Computer Science Department, Brandeis University, Waltham, Massachusetts, 1985.
[9] Richbourg, R. F., Rowe, N. C., Zyda, M. J., and McGhee, R., "Solving Global Two-Dimensional Routing Problems Using Snell's Law and A* Search", Proceedings IEEE International Conference on Robotics and Automation, pp. 1631-1636, Raleigh, North Carolina, 1987.
[10] Rowe, N. C., and Richbourg, R. F., "An Efficient Snell's-Law Method for Optimal-Path Planning Across Multiple Two-Dimensional Irregular Homogeneous-Cost Regions", to appear in International Journal of Robotics Research, 1990.
This appendix contains the statements of six theorems from [1] which specify the algebraic form of six commonly occurring boundaries. Proofs of these theorems follow directly from trigonometric identities, principles of optimal paths, and algebraic manipulations.
THEOREM 1: (Boundary between two regions with paths which go initially to two different points) Given goal point G and two adjacent homogeneous-behavior regions of cost rate r whose region roots are points @V sub 1 @ and @V sub 2 @, costs @c sub 1 = |(V sub 1 G)*|@ and @c sub 2 = |(V sub 2 G)*|@ (the costs of optimal paths from @V sub 1 @ and @V sub 2 @ respectively) where without loss of generality it is assumed that @c sub 2 > c sub 1 @, the boundary between regions 1 and 2 is a portion of the hyperbola branch which is closer to @ V sub 2 @ than to @V sub 1 @, and is described by
(Equation 1)
@{{x sup 2 } over {a sup 2 }} - {{y sup 2 } over {b sup 2 }} = c sup 2@
where @a = {(c sub 2 - c sub 1 )} over 2 , c = r cdot d(V sub 1 ,V sub 2 )@, and @b sup 2 = c sup 2 - a sup 2 @, and where the x-axis is oriented along the line segment @V sub 1 V sub 2 @ with the origin at a point half-way between @V sub 1 @ and @V sub 2 @ .
THEOREM 2: (Boundary between a region with paths which go
initially to a point, and a region with paths which go to and travel
along a linearly-traversed-edge, or "road") Given goal point G
and two adjacent homogeneous-behavior regions with cost-rate @r sub 0 @,
one region having point U as root and the other having linearly-traversed
edge VW as root, where VW is a sub-segment of some terrain-feature
edge such that OPL(V) = [W | OPL(W)] and the cost-rate along the edge
is @r sub vw @, (for example, a road segment where paths leave the
road from point W), the boundary between them is a portion of the
curve
(Equation 2)
@y sup 2 = 4 p x@,
where p is defined as follows. From W extend a ray @WW sub d @ away from region 2 (i.e., no point on @WW sub d @ lies in region 2) such that angle @VWW sub d = pi over 2 + psi @, and the distance between @W@ and @W sub d @ is @{(c sub w - c sub u)} over {r sub 0} @. Let point @U sub d @ be the point such that line @UU sub d @ is parallel to @WW sub d @, and the line @U sub d W sub d @ is perpendicular to line @UU sub d @. Let point O be the point on line @UU sub d @ equidistant between @U@ and @U sub d @. Then the coordinate axes are the line @UU sub d @ (x-axis with U in the positive x direction) and the line through O parallel to @U sub d W sub d @ (y-axis with @W sub d @ in negative y direction), and @p = {(c sub w - c sub u )} over {r sub 0 }@, where @ psi = sin sup -1 r sub vw over {r sub 0 }@ is the critical angle, @c sub w = |(WG)*| @, and @c sub u = |(UG)*| @ (the costs of optimal paths to goal point G from W and U respectively). Note that the x-axis is the parabola axis and the line @U sub d W sub d @ is the directrix.
.br THEOREM 3: (Boundary between regions having paths which go to and travel along two different linearly-traversed edges, or "roads") Given goal point G and two adjacent homogeneous-behavior regions with cost-rate @r sub 0 @, one region having linearly-traversed edge XY as root and the other having linearly-traversed edge VW as root, where XY and VW are sub-segments of terrain-feature edges such that OPL(X) = [Y | OPL(Y)], OPL(V) = [W | OPL(W)] and the cost-rates along the edges are @r sub xy @ and @r sub vw @ respectively, (for example, two road segments where paths leave road XY from point Y or leave road VW at point W), the boundary between them is a segment of line L defined as follows. Let @D sub xy @ be the line which forms angle @ psi sub xy @ with line XY, is distance @ c sub y @ from point Y, and lies on the side of XY which does not include the region of which XY is the root. Let @D sub vw @ be the line which forms angle @ psi sub vw @ with line VW, is distance @c sub w @ from point W, and lies on the side of VW which does not include the region of which VW is the root. Let @P sub 0 @ be the point of intersection of @D sub xy @ and @D sub vw @, and let @ alpha @ be the angle between line XY and line VW. Then the boundary lies on line L, which is the line through point @P sub 0 @ which lies at an angle @ {( alpha + psi sub vw + psi sub xy )} over 2 @ with both @D sub xy @ and @D sub vw @.
THEOREM 4: (Boundary between two regions having paths which cross two different edges) Given goal point G and two adjacent homogeneous-behavior regions with cost-rate @r sub 0 @, one region having Snell's-Law edge VW and the other having Snell's-Law edge XY, where paths which cross VW go directly to point U at cost-rate @r sub vw @, paths which cross XY go directly to point Z at cost-rate @r sub xy @, and where the total cost from U to the goal is @c sub u @ and from Z to the goal is @c sub z @, the boundary between them consists of points P such that the distance from P to edge VW is @x sub 2 @, the distance from VW to U is @x sub 1 @, the distance from point P to edge XY is @y sub 2 @, the distance from XY to Z is @y sub 1 @, the angle of incidence of the path from P across edge VW to U is @ theta sub 2 @, the angle of refraction is @theta sub 1 @, the angle of incidence of the path from P across edge XY to Z is @ theta sub 4 @, and the angle of refraction is @ theta sub 3 @, where the seven equations of Equation Set 4 are satisfied.
(Equation Set 4)
x sub 1 = {d sub 1 sin gamma } over {cos theta sub 1 }
, y sub 1 = {d sub 0 sin beta } over {cos theta sub 3 },
y sub 2 = {sin alpha} over {sin theta sub 4 } ({d sub 1 cos ( theta sub
1 - gamma )} over {cos theta sub 1 } - {cos ( theta sub 2 + alpha )}
over {cos theta sub 2 } (
{ { {d sub 0 cos ( { theta sub 3 - beta } ) } over {cos theta sub 2 } -
{ {d sub 1 cos ( { theta sub 1 - gamma } ) cos ( { theta sub 4 + alpha } ) }
over { cos theta sub 1 cos theta sub 4 } } }
over { 1 -
{ { cos ( { theta sub 2 + alpha } ) cos ( { theta sub 4 + alpha } ) }
over { cos theta sub 2 cos theta sub 4 } } } } ))
x sub 2 = { {d sub 0 sin alpha cos ( { theta sub 3 - beta } ) } over {cos theta sub 2 cos theta sub 3 } -
{ {d sub 1 cos ( { theta sub 1 - gamma } ) cos ( { theta sub 4 + alpha } ) }
over { cos theta sub 1 cos theta sub 4 } } }
over { 1 -
{ { cos ( { theta sub 2 + alpha } ) cos ( { theta sub 4 + alpha } ) }
over { cos theta sub 2 cos theta sub 4 } } } )).
Boundary Condition:
r sub vw x sub 1 + r sub 0 x sub 2 = r sub xy y sub 1 + r sub 0 y sub 2
Snell's Law for edge VW:
r sub vw sin theta sub 1 = r sub 0 sin theta sub 2
Snell's Law for edge XY:
r sub xy sin theta sub 3 = r sub 0 sin theta sub 4
where @ theta sub 1 @ and @ theta sub 3 @ are the dependent and independent variables.
THEOREM 5: (Boundary between a region with paths which go to and travel along a linearly-traversed edge ("road") and a region with paths which cross an edge) Given goal point G and two adjacent homogeneous-behavior regions with cost-rate @r sub 0 @, one region having linearly-traversed edge VW as root, and the other having as root Snell's-Law edge XY, where VW is a sub-segment of some terrain-feature edge such that OPL(V) = [W | OPL(W)] and the cost-rate along the edge is @r sub vw @, (for example, a road segment where paths leave the road from point W), and where paths which cross XY go directly to point Z at cost-rate @r sub xy @, and where the total cost from W to the goal is @c sub w @, and from Z to the goal is @c sub z @. The boundary between the regions consists of points P such that the six equations of Equation Set 5 are satisfied.
(Equation Set 5)
y sub 1 = {d sub 3 sin beta } over {cos theta sub 1 } ,
y sub 2 = x sub 1 {sin alpha } over {cos theta sub 2 } - x sub 2
{cos { ( psi + alpha } ) } over {cos theta sub 2 } + d sub 2 {sin gamma }
over { cos theta sub 2 }
x sub 2 = { d sub 2 (cos ( theta sub 2 + gamma )(r sub 0 sin alpha - r
sub vw cos theta sub 2 )+r sub 0 sin gamma cos ( theta sub 2 - alpha )) } over
{ sin ( theta sub 2 - alpha - psi )r sub vw cos theta sub 2 + r sub 0
cos ( theta sub 2 - alpha )(sin ( theta sub 2 - alpha - psi ) + r sub 0 (cos
theta sub 2 + cos ( theta sub 2 - alpha ))) }
{ d sub 3 cos theta sub 2 (r sub 0 sin alpha cos beta + r sub xy sin
beta cos ( theta sub 2 - alpha )) + ( c sub z - c sub w ) cos theta sub 2
cos ( psi - alpha ) } over
{ sin ( theta sub 2 - alpha - psi )r sub vw cos theta sub 2 + r sub 0
cos ( theta sub 2 - alpha )(sin ( theta sub 2 - alpha - psi )+r sub 0 (cos
theta sub 2 + cos ( theta sub 2 - alpha ))) }
x sub 1 = { ( { r sub 0 sin alpha } over {cos ( theta sub 2 - alpha ) }
+ r sub 0 ( { cos theta sub 2 + cos ( psi + alpha ) } over { sin ( theta
sub 2 - alpha - psi ) } - 1))(d sub 2 cos ( theta sub 2 + gamma )+d sub
3 cos beta cos theta sub 2 ) } over
{ r sub vw cos theta sub 2 + r sub 0 cos ( theta sub 2 - alpha )({cos
theta sub 2 + cos ( gamma + alpha ) } over { sin ( theta sub 2 - alpha -
psi ) } - 1 ) }
+ { d sub 2 r sub 0 sin gamma + d sub 3 ( {r sub vw cos beta cos sup 2
theta sub 2 } over { cos ( theta sub 2 - alpha ) } + r sub xy sin beta
cos theta sub 2 ) + (c sub z - c sub w ) cos theta sub 2 } over
{ r sub vw cos theta sub 2 + r sub 0 cos ( theta sub 2 - alpha )({cos
theta sub 2 + cos ( gamma + alpha ) } over { sin ( theta sub 2 - alpha -
psi ) } - 1 ) }
Snell's Law condition for edge XY:
r sub xy sin theta sub 1 = r sub 0 sin theta sub 2Snell's Law condition for edge VW:
sin psi = r sub vw over r sub 0
THEOREM V-0.6: (Boundary between two regions each having paths which cross two edges) Given goal point G and two adjacent homogeneous-behavior regions with cost-rate @r sub 0 @, one region having Snell's-Law edge VW and the other having Snell's-Law edge RS, where paths which cross VW go from there at cost-rate @r sub vw @ directly to a Snell's-Law crossing at edge XY, and then go at cost-rate @r sub xy @ directly to point @Z sub 1 @; paths which cross RS go from there at cost-rate @r sub rs @ directly to a Snell's-Law crossing at edge TU, and then go at cost-rate @r sub tu @ directly to point @Z sub 2 @, and where total cost from @Z sub 1 @ to the goal is @c sub 1 @ and from @Z sub 2 @ to the goal is @c sub 2 @, the boundary between them consists of points P such that the path distance from P to edge VW is @y sub 3 @, the path distance from VW to XY is @y sub 2 @, the path distance from XY to point P is @y sub 1 @, the path distance from point P to edge RS is @x sub 3 @, the path distance from RS to TU is @x sub 2 @, and the path distance from TU to @Z sub 2 @ is @x sub 1 @, where the fourteen equations of Equation Set 6 are satisfied.
(Equation Set 6)
x sub 1 = {d sub 7 sin beta sub 1 } over { cos theta sub 8 }
, y sub 1 = {d sub 5 sin beta sub 1 } over { cos
theta sub 1 } ,
x sub 2 = { sin alpha sub 3 } over { cos theta sub 6 }
(d sub 4 - {d sub 7 cos ( beta sub 2 - theta sub 8 ) } over { cos theta
sub 8 } ) , y sub 2 = { sin alpha sub 1 } over { cos theta
sub 3 } (d sub 1 - {d sub 5 cos ( beta sub 1 - theta sub 1 ) } over { cos
theta sub 1 } ) ,
x sub 3 = - { sin ( alpha sub 3 + gamma sub 1 ) } over {cos ( theta sub
5 + alpha sub 4 + gamma sub 1 ) } (d sub 3 - {d sub 4 cos theta sub
7 } over { sin theta sub 6 } + {d sub 7 cos ( beta sub 2 - theta sub 8
) cos theta sub 7 } over {cos theta sub 8 } ) ,
y sub 3 = { sin gamma sub 1 } over { cos ( theta sub 4 - gamma sub 1
) } (d sub 2 - {d sub 1 cos theta sub 2 } over {cos theta sub 3 } +
{d sub 5 cos ( beta sub 1 - theta sub 1 ) cos theta sub 2 } over {cos
theta sub 1 } ) ,
{cos ( theta sub 4 - gamma sub 1 ) } over { cos ( theta sub 5 + alpha sub
4 + gamma sub 1 ) } =
{d sub 3 - {d sub 4 cos theta sub 7 } over {
sin theta sub 6 } + {d sub 5 cos ( beta sub 2 - theta sub 8 ) cos theta
sub 4 } over {cos theta sub 8 } }
over
{d sub 3 - {d sub 4 cos theta sub 7 } over {
sin theta sub 6 } + {d sub 7 cos ( beta sub 2 - theta sub 8 ) cos theta
sub 7 } over {cos theta sub 8 } }
Boundary Condition:
r sub 0 y sub 3 + r sub vw y sub 2 + r sub xy y sub 1 = r sub 0 x sub 3 + r sub rs x sub 2 + r sub tu x sub 1Snell's Law:
r sub vw sin theta sub 2 = r sub xy sin theta sub 1
r sub 0 sin theta sub 4 = r sub vw sin theta sub 3
r sub rs sin theta sub 7 = r sub tu sin theta sub 8
r sub 0 sin theta sub 5 = r sub rs sin theta sub 6
Trigonometric Identities:
theta sub 3 = alpha sub 1 - theta sub 2 theta sub 6 = alpha sub 3 - theta sub 7