Finding Optimal-Path Maps

Finding Optimal-Path Maps
for Path Planning Across Weighted Regions

Neil C. Rowe and Robert S. Alexander

Computer Science Department, Code CS/Rp

U.S. Naval Postgraduate School Monterey, CA 93943 USA

Abstract

Optimal-path maps tell robots or people the best way to reach a goal point from anywhere in a known terrain area, eliminating most of the need to plan during travel. We address the construction of optimal-path maps for two-dimensional polygonal weighted-region terrain, terrain partitioned into polygonal areas such that the cost per unit distance traveled is homogeneous and isotropic within each polygon. This is useful for overland route planning across varied ground surfaces and vegetation. We propose a new algorithm that recursively partitions terrain into regions of similar optimal-path behavior, and defines corresponding "path subspaces" for these regions. This process constructs a piecewise-smooth function of terrain position whose gradient direction is everywhere the optimal-path direction, permitting quick finding of optimal paths. Our algorithm is more complicated than the current path-caching and wavefront-propagation algorithms, but gives more accurate maps requiring less space to represent. Experiments with an implementation confirm the practicality of our algorithm.

This paper appeared in the International Journal of Robotics Research, 19, 2 (February 2000), pp. 83-95, with elaborating additions from [Rowe and Alexander, 1997]. The equations were redone for greatly improved clarity in 2008.

This work was supported in part by the U.S. Army Combat Developments Experimentation Center under MIPR ATEC 88-86. This work was also prepared in part in conjunction with research conducted for the Naval Air Systems Command and funded by the Naval Postgraduate School.

Introduction

Paths that are optimal with respect to cost or safety are often desirable for robots or people operating in a known environment. Computing such paths for complex and interesting parts of the real world requires significant effort. But optimal paths computed long before their use could answer a frequent complaint that optimal-path planning takes too long to be relevant to real-world problems. A library of precomputed optimal paths could quickly route automated sentry vehicles for minimum energy expenditure in varying circumstances, provide fast escape routes for robots in dangerous environments, or permit a robot that wanders off a route to always find their way back. They can also be useful for virtual terrain like a robot configuration space.

We investigate here the problem of systematically precomputing a large or infinite number of optimal paths to a goal point for known two-dimensional isotropic terrain consisting of polygonal "weighted regions" [Hwang and Ahuja 1992; Mitchell 1988; Rowe and Richbourg 1990], among which a mobile agent of negligible size can travel freely except for designated impassable "obstacle regions." A "weighted region" is an area homogeneous with respect to cost per unit distance for travel, and where the cost per distance does not vary with direction ("isotropic" terrain). For example, weighted regions can distinguish forest from grasslands in overland terrain, or rocky terrain from smooth terrain, or terrain visible to an overhead enemy from terrain invisible. The cost of a path on weighted-region terrain is where is cost per unit distance ("weight") on the ith region in the path, and where is the distance traveled through the ith region. Snell's Law determines how optimal paths turn when they cross boundaries between weighted regions of different cost per unit distance [Rowe and Richbourg 1990], and says that , where is the cost per unit distance in region i and is the angle between the path and the normal to the boundary. Because Snell's Law applies to optics and light rays follow Fermat's Principle of using the shortest path between two points, solutions of the weighted-region problem also help in designing lenses and other optical systems. They are also useful for planning permanent linear features like electric lines. Useful results are still obtainable from weighted-region modeling even when cost-per-distance has significant variation as in [Mobasseri 1990].

For our work reported here we assume that the weighted regions modeling some two-dimensional terrain have already been created. For instance, U.S. Defense Mapping Agency data gives vegetation and surface-cover regions for much of the world at a 100-meter resolution. Other work of ours has generalized these methods to three-dimensional space, but here we shall consider only a planar two-dimensional world.

Specifically, we generalize here the common problem in robotics of finding an optimal path between two points to the "optimal-path-map" problem of computing all optimal paths to a given goal point. Formally, an optimal-path map for a known two-dimensional terrain area with a known goal point is a function o(x,y) whose values describe how to best reach the goal from location (x,y). (Alternatively, an optimal path map could describe how best to get anywhere in an area from some fixed start point.) This o must be defined for every (x,y) in the terrain area, not just for a finite set of places, so the problem does not immediately reduce to graph search. The value of o can be defined as a vector so that o creates a vector field on some terrain. It can be made a potential field in the physics sense by setting the vector magnitude proportional to cost to the goal, but this is not helpful: We cannot exploit superposition effects and contour invariants as with electromagnetic fields. Many current potential-field methods for path planning do use superposition, but yield heuristic paths with no guarantees of optimality.

Previous work on true optimal-path maps has investigated restricted cases. While many optimal-path planners do a thorough search, this search is almost always over a finite set of locations; thus the data structures created by path-planning searches do not automatically "solve" the optimal-path-map problem of assigning paths to an infinite number of starting points. [Payton and Bihari 1991] does suggest approximating a vector field by the results of a wavefront propagation on a uniform grid of paths about a start point, an idea we will discuss in section 2. [Hwang and Ahuja 1992] and [Mitchell 1993] give algorithms to find "shortest-path maps" (optimal-path maps for terrain with obstacles only), using a recursive decomposition of the terrain into wedges like in [Mitchell and Papadimitriou 1991]. In [Mitchell 1993] these wedges or "wavelets" partition the terrain into subregions of similar optimal-path behavior, exploiting the property of terrain with only obstacles that discontinuities in optimal-path behavior occur only along straight-line and hyperbola segments. This work exploits similarities to the construction of Voronoi (closest-point) diagrams as in [Chew and Drysdale 1985]. Other work on restricted cases of shortest-path maps is [Lee and Preparata 1984] and [Reif and Storer 1994].

Unfortunately, generalizing shortest-path-map work to the weighted-region problem is not straightforward. [Chen et al 1995] provides an algorithm to find all optimal paths between members of a finite set of points on weighted-region terrain, but that is a different problem. The "generalized Voronoi diagram" of [Chew and Drysdale 1985] and in [Lee and Drysdale 1981] requires convexity of equi-cost contours, something that rarely occurs in the weighted-region problem, and "weighted Voronoi diagrams" address an essentially unrelated problem. (Despite some misleading terminology, [Mitchell and Papadimitriou 1991] does not solve the weighted-region optimal-path-map problem because it does not find behavioral boundaries in weighted regions as in section 4.2 below.) Unfortunately, it appears that no spatial distortion of a weighted-region terrain will convert an optimal-path-map weighted-region problem on it into a Voronoi problem, because the abrupt discontinuities in cost-per-distance on boundaries sabotage attempts to define a Euclidean distance metric unless we abandon most of the usual meaning of "distance." Some work such as [Schoppers 1989] discusses generalizations of optimal-path maps called "universal plans", but such generalized problems are much harder combinatorially. Our own previous work [Alexander 1989; Alexander and Rowe, 1989] solved the optimal-path-map problem for specialized "decomposable weighted-region terrain" in which homogeneous-cost regions were separated from one another and embedded in a single "background-cost" region. Then optimal-path maps for regions of the terrain can be independently constructed and merged to produce a complete optimal-path map, something not possible on general weighted terrain.

It should be noted that unlike shortest-path maps and many other problems in computational geometry, optimal-path maps for the weighted-region problem can only be approximated even for completely known terrain. This is because the finding the optimal path to a point across a weighted-region boundary requires iteration when Snell's Law is inverted this way, and the resulting map is best defined with approximate "behavioral boundaries" (see section 4.2). However, it is still fair to call these maps "optimal" because the error can be bounded unlike with potential-field approaches.

This paper will first examine the two most obvious ways to create optimal-path maps: precomputing a set of optimal paths to a goal point (section 2), and propagating a "wavefront" around a start point over a grid of evenly-spaced points (section 3). Both are "skeleton" approaches [Hwang and Ahuja 1992] that construct a framework of good paths to which new start points are related, and both have disadvantages. We then propose a new algorithm (section 4) that subdivides the terrain into areas of qualitatively similar optimal-path behavior; we can then find what area a start point is in, retrieve its qualitative behavior, and build an optimal path quickly. Fig. 1 compares the three approaches.

Algorithm	Approximation from cached paths (section 2)	Wavefront propagation on a square grid (section 3)	Recursive wedge (path-subspace) partition (section 4)
Worst-case map-building time complexity
Average-case map-building time complexity
Map-building space complexity
Worst-case execution time complexity
Average-case execution time complexity
Execution-time space complexity
Maximum error (found-path cost minus optimal-path cost)		representation error	Small, set by Snell's Law tolerance and distorted-cone approximation
Other disadvantages	Hard to guess points to cache	Unreasonably jagged paths	A more complex algorithm

m: Number of cached points or grid cells
v: Number of vertices in the weighted-region graph
: Maximum finite cost-per-distance for a grid cell
d: Least-common multiple of all cost-per-distances
: Cost from start point to the nearest cache or cell-center neighbor
: Cost from start point to the goal on a path

Figure 1: Comparative summary of the three algorithms for finding optimal-path maps, based on Theorems 2.1 and 3.1 of [Rowe and Alexander, 1997] and Theorem 4.3 of this paper.

The path-caching approach to optimal-path maps

A simple way to approximate an optimal-path map for a particular goal point is to find paths to that goal from a variety of start points, store the paths, and interpolate somehow between them when asked to find an optimal path from a new start point. Evenly-spaced start points are easiest. Fig. 2 shows an example, summarizing 1656 runs of an optimal-path planner reported in [Rowe 1990]. The terrain is a homogeneous medium-cost-rate background region upon which have been overlain some "road" segments (the solid black lines) of half the cost-per-unit-distance of the background region, "river" segments (the gray shaded lines) of a 2.2 times the cost-per-unit-distance of the background, and an impassable "obstacle" region (the solid black triangle). The short lines represent the initial direction of the optimal path at evenly-spaced points to a goal point in the lower right. The effectiveness of such a map greatly depends on the quality of the path planner. The planner used for Fig. 2 reasons geometrically about terrain features and gives true optimal paths.

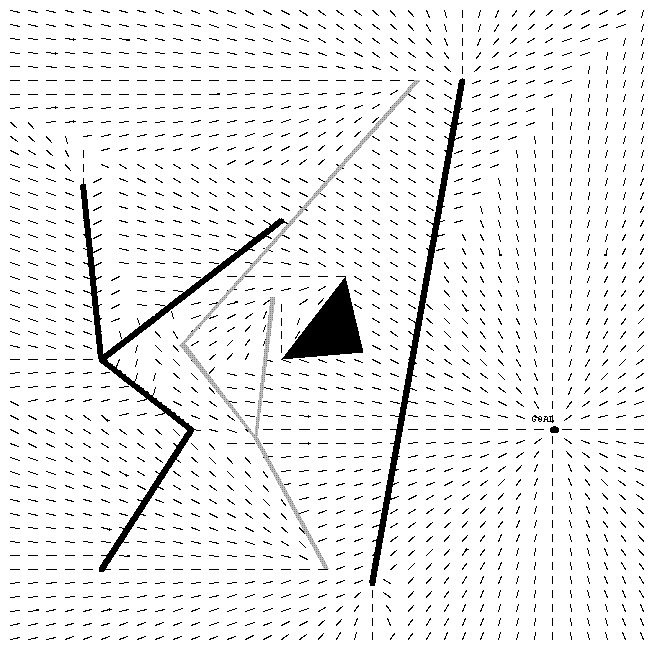
Figure 2: An example optimal-path field for a goal point on the right. The thick long lines are roads (of low cost to follow), the gray linear structure is a fence (of high cost to cross), the black triangle is an obstacle (impossible to cross), and the small lines indicate optimal-path direction.

The simplest way to use such preanalysis to reach the goal G from an arbitrary starting point S is to head directly to the nearest preanalyzed point N (nearest in cost, to be more precise) and follow its path to G. The cost of such a path is the cost S to N, call that , plus the cost of precomputed optimal path N to G, call that , and this is an upper bound on the cost of an optimal path from S to G. A lower bound is then because otherwise the optimal path from N to G could go through S and be less costly than , a contradiction.

The time and space complexity for this algorithm shown in Fig. 1 were obtained in Theorem 2.1 of [Rowe and Alexander, 1997]. A key weakness of the algorithm is the tricky task of choosing the cache points to obtain a desired level of accuracy. The appropriate density may vary considerably over the picture, as Fig. 2 suggests. But we cannot properly choose this density until we have found many paths, since the features that critically control path behavior in some area may lie quite some distance away. So to be safe we must find many more paths than necessary, then store only the initial path directions of those that are not predictable from their neighbors. This will increase preanalysis time considerably.

[The following three paragraphs do not appear in the journal version of this paper but appear in [Rowe and Alexander, 1997] ]

Theorem 2.1: The above algorithm for finding a near-optimal path to a goal from an arbitrary start point, using a finite set of cached paths, requires preanalysis space, execution-time space, preanalysis time in the worst case, preanalysis time in the average case, execution time in the worst case, and execution time in the average case, where v is the number of vertices in the polygonal representation of the weighted regions, and m is the number of cached paths. Proof: [Mitchell and Papadimitriou 1991] presents an algorithm for the weighted-region problem with a single start point and single goal point which is in time for a fixed level of accuracy; we just need run this m times for preanalysis. Then run-time work for a given start point is to find the nearest neighbor in cost to the start point.

For the average case, the weighted-region path-planning algorithm of [Rowe and Richbourg 1990] was shown both analytically and experimentally to require steps each involving a numerical optimization for which substeps appear experimentally to be always sufficient. This gives for the preanalysis for an optimal-path map in the average case. As for average execution time, the search for the nearest neighbor is similarly in general. But if the cached points are closely enough spaced so that the nearest neighbors are usually within the same weighted region, something usually easy to arrange, then the path to the nearest neighbor is a usually a straight line and requires time.

The space required for map building can be reused by each start point. The space must be for wedge-boundary paths of piecewise-linear pieces each since there are edges and an edge can be visited at most times [Rowe and Richbourg 1990]. Hence preanalysis space is . We must store m cached paths at execution time, and each is size as in preanalysis. Hence execution time requires space. QED.

An optimal path P1 from S1 to G never should cross an optimal path P2 from S2 to G, although they can merge, because P1 would then be no better than a path that followed P1 to the intersection point and then followed P2 to G. However, exploiting this to rule out terrain for later optimal-path consideration seems to require repeated comparison of terrain features to paths. Section 4 will present a better way.

[The following four paragraphs do not appear in the journal paper but appear in [Rowe and Alexander, 1997] ]

Some further post-hoc analysis can be done with cached optimal-path information at sample points, to provide guarantees of the qualitative nature of the optimal path at all start points within a region. Optimal paths for the weighted-region problem must be straight within weighted regions because there is no reason to turn there [Rowe and Richbourg 1990]. So label all polygonal region edges and vertices with unique identifiers; then define the qualitative behavior B(P) of an optimal path P as the sequence of edge and vertex identifiers in that path. The following theorem describes a region of start points in which B(P) is constant.

Theorem 2.2: On weighted-region terrain, let P be an optimal path from point S to point G. Let the cost of P be , the qualitative behavior of P be B(P), and the cost of the minimum-cost path S-to-G having a different qualitative behavior than B(P) be . Suppose point S is in a region R of cost-per-unit-distance , and suppose the path P leaves R at point E at distance D from S. Then B(P) is also the optimal behavior to G from any point A within an ellipse whose foci are S and E, whose major axis is length provided the ellipse does not intersect any cost-region boundaries other than the one containing E. Proof: We do not know in what direction the second-best behavior from S to G will head from S, but in the worst case A will be precisely in this direction, and hence heading toward A will decrease its cost by the distance between S and A times ; so the cost of the second-best behavior from S to G will decrease by at most this same cost. At the same time, the cost of following B(P) from S to A (and then straight to E, and then following the original path from S to G from there) can be increased no more than from the definition of an ellipse. The condition that no other region edges appear in the ellipse is necessary to ensure that paths in R from an ellipse focus to the ellipse boundary cross any edges unless first crossing E's edge. QED.

An important consequence of Theorem 2.2 is that whenever it applies to determine B(P) for some point Q, determination of the true optimal path from Q to goal G is considerably faster, since we only need adjust the crossing points on a set of known edges to satisfy Snell's Law.

Another way to approximate paths from cached optimal-path information would be to store only the first direction of the optimal path to the goal for each preanalyzed point. Then average the optimal-path directions at the corners of the smallest polygon of preanalyzed points that encloses the given start point. Then move forward in this direction, interpolate among the new neighbors, and so on until you reach the goal. In other words, approximate a field line from neighbor directions. This works well in portions of the terrain where the field direction either does not change much, as in the upper right of Fig. 2, or changes in a smooth way, as in the upper left. But interpolation cannot give guaranteed-optimal paths, or even be guaranteed to come close to optimal paths. Four points are usually insufficient to represent the complex functions that determine the optimal-path direction for even greatly simplified terrain, since rarely are all four points directed toward a single intermediate point, and nonlinear phenomena like Snell's Law distort the directions. Interpolation can be improved by taking the sixteen closest neighbor points, but this does not solve the problem. Furthermore, there can be unexpected changes in optimal-path direction between nearby points. For instance at the top of Fig. 3, optimal-path direction reverses abruptly near a road end; and in the middle, optimal-path direction temporarily aims around an obstacle instead of its usual direction. Interpolation between the first and third starting points vertically, or between the third and fifth, would infer a wrong direction. The terrain features that cause such failures of interpolation need not be close, so it is hard to anticipate when interpolation will be good. And these errors can mount as one proceeds to the goal following these interpolated directions.

Wavefront-propagation methods for constructing optimal-path maps

Wavefront propagation is a fast way to get approximate optimal-path directions for many evenly-spaced points. It works across a terrain grid of square uniform-size cells by propagating a wavefront at a uniform-cost rate in all directions [Kambhampati and Davis 1986; Mitchell et al 1986; Parodi 1985]. (Some wavefront-propagation methods use nonuniform grids, but this is uncommon, significantly more difficult to implement, and requires human judgment as to the appropriate resolution for different areas of terrain.) Usually "backpointers" are set whenever the wavefront reaches a new cell, indicating from what direction the "wave" came, though some algorithms set the pointers only for cells meeting certain criteria (like those that use A* search [Nilsson 1980] to improve performance). These backpointers can be used to build an optimal-path map, and they can be interpreted as optimal-path directions at the centers of the grid cells. To use these directions more easily, the step-size for reconstructing paths can be a function of direction so that each step takes you to the center of another cell; so for the usual case of eight directions of propagation on a square grid, the step size is 1 cell width for horizontal and vertical motion, for diagonal motion. A detour to a nearby cell center must still be done for a start point that does not lie at a cell center. Chapter 3 of [Alexander 1989] discusses algorithm details.

Wavefront propagation for the weighted-region problem has several disadvantages. Restricting vectors to a finite set of directions usually prevents travel at optimal path headings, since even when terrain feature boundaries are horizontal and vertical and traversal costs form integer ratios, Snell's Law makes optimal directions unevenly spaced. (Note the subtle variations in path direction in Fig. 2 that a wavefront algorithm could not produce.) So the paths found make abrupt turns at rather arbitrary places. This can be improved, at the risk of losing path optimality, by local smoothing of segments of the crooked portions of the path [Mitchell et al 1986]. The effect is due to the digitization bias in the propagation calculation method, and means there can be a many theoretically optimal paths where better terrain modeling would permit only one. Note that the bias does not decrease as the grid size decreases since the geometry remains the same at finer resolutions. [Rowe and Richbourg 1990] shows that for eight-direction propagation (the most common form) in a square grid, this type of cost error of a supposedly optimal path found by the method can be up to 7.6% more than the true optimal path cost due to the increased distance that could be traveled. But again, this assumes the path is followed exactly, which can be hard for people and even robots.

In addition, as with path caching, an extra error is added in getting from the start point to the center of a grid cell. And there is a third source of error, representation error with the grid. Weighted-region polygon boundaries rarely coincide with square grid cells, so some cells will include regions of more than one cost-per-distance. If an average, weighted by area within the square, is used to compute the cell cost-per-distance, the accumulated error in traversing that cell could be very large if cost-per-unit-distance varies considerably on the terrain. An example would be a fence of high traversal cost-per-distance running north-south: Should we set the cost of a cell over it to a high or low value? If high, we are unfair to north-south traversals; if low, we are unfair to east-west traversal. This problem does not occur with a polygonal region representation, for then the fence could be a separate narrow region.

So there are three independent sources of error in wavefront propagation, the first of which does not improve with increased resolution m, and the third of which can give potentially big errors. Even if the terrain knowledge comes directly in the form of a grid of cost-per-distance values obtained from satellite imaging, and wavefront propagation is done on the raw grid without any cell aggregation, the resulting optimal-path map only finds paths connecting centers of grid cells. Thus wavefront propagation is not a true method for finding optimal paths. Theorem 3.1 of [Rowe and Alexander, 1997] provides time, space, and accuracy analysis of wavefront propagation, which we include in Fig. 1.

Another disadvantage of wavefront-propagation "optimal"-path maps is the amount of data generated: backpointers for evenly-spaced points across the whole map, even in uninteresting parts of the terrain. An improvement is to store only "behavioral boundaries" between "behavioral regions", regions of significantly different optimal-path direction, and store a single average path direction for each behavioral region. To study this, [Alexander 1989] modified a wavefront-propagation program to do extra work on each propagation into a cell that is already on the wavefront. Several heuristics were tried for marking behavioral boundaries; the best found was to draw a boundary when the backpointer chains of adjacent cells have different lists of terrain features (regions and edges) that they cross. But spurious boundaries can occur with this heuristic, and boundaries were often ugly (distorted and jagged) due to the digitization bias.

[The following paragraph does not appear in the journal paper but appears in [Rowe and Alexander, 1997]]

Theorem 3.1: For wavefront propagation on a square grid of m cells, d the least common multiple of all cost-per-distance values, and the maximum finite (i.e. excluding obstacles) cost-per-distance, building the approximate optimal-path map for a weighted-region problem requires preanalysis time, execution time, and space, in both the worst case and the average case. Proof: The m cells will form a by square grid, for which steps are required to propagate the wavefront across the entire grid, since the least common multiple of the cost-per-distance values must be the cost increment for wavefront expansion to ensure output correctness, and since an optimal path could be cells long in the worst case. Each step requires update of a wavefront of size since it could be highly irregular. So the whole map-building is . Then use of the resulting map requires finding the nearest cell center to the start point, but that is easy on a square grid, and furthermore the route there is through a single homogeneous cell and hence must be a straight line, so the execution time is to follow the pointers to the goal. There are m grid cells, and each need store just a cost and one backpointer (since all path segments are between cell centers), and the agenda size is , so storage is for both preanalysis and execution time. The times for the average case are no different from the worst case, since the same operations must be performed to propagate independent of the cost-per-unit-distances on the graph or to assemble paths. QED.

Optimal-path maps by wedge partition of the terrain

Another way to construct optimal-path maps is to reason geometrically about terrain areas. This approach is used by some algorithms for the fixed-start fixed-goal weighted-region problem [Mitchell and Papadimitriou 1991; Rowe and Richbourg 1990], and is called "continuous-Dijkstra" in [Mitchell and Papadimitriou 1991]. The idea is to partition terrain in equivalence classes with respect to optimal-path behavior.

Since a straight line is the shortest distance between two points, and path cost is proportional to path distance in a weighted region, optimal paths across weighted-region terrain must be piecewise-linear, turning only on weighted-region boundaries. Then a qualitative description of an optimal path over weighted-region terrain is its "behavior" B(P), the list of the edges and vertices of the polygonal weighted regions encountered in order along the path. For a particular start point, starting direction, and B(P), it is straightforward to "ray trace", obeying Snell's Law at each edge, to find an optimal path to the goal. We can also address the inverse problem of finding the proper starting direction given a start point, goal point, and B(P) such that the goal point is reached by an optimal path from the start point; this must be solved by iteration, and it helps that the path cost is shown convex in [Rowe and Richbourg 1990].

Places in the terrain where B(P) changes are thus behavioral boundaries partitioning terrain into behavioral regions. (Such boundaries generalize Voronoi-diagram "bisectors" since the behavior change does not necessitate a discontinuity in optimal-path direction.) Finding them would accomplish most of the work of constructing an optimal-path map. To do this, we will work simultaneously in two separate spaces, the terrain space and the space of all possible paths to a particular goal point. We will recursively partition the latter into subspaces called "wedges" until each weighted-region segment corresponding to each part of each wedge has a single B(P). We shall call such nice wedges "well-behaved path subspaces" or WBPSs. Some small additional work can then calculate the behavioral boundaries in wedge boundaries and wedge overlaps.

Cost surfaces

It helps to envision three-dimensional cost surfaces to understand optimal-path maps. Let c(x,y) represent the cost of getting from (x,y) in the map plane to the goal point along an optimal path. Let the o(x,y) of section 1 be defined as a vector with direction the direction of optimal travel at (x,y), and magnitude the cost-per-distance there in that direction. Then o is the gradient of c within weighted regions (since the optimal direction decreases the cost to the goal faster than any other direction), and can be found by path planning to vertices otherwise.

Cost surfaces are simpler within WBPSs than in arbitrary wedges since WBPSs are generally-narrow corridors wherein all the paths are subject to similar constraints. Thus our strategy will be to partition optimal paths into WBPSs and then compute cost surfaces for the terrain enclosed. Cost surfaces within each weighted-region portion of a WBPS for the weighted-region problem are of only three types: cone, plane, and distorted cone.

A cone cost surface occurs around a "converging vertex" in a weighted region when optimal paths in a WBPS converge directly on the vertex with a range of headings. An example is the cost of optimal paths with goal point C1 of Fig. 3 and start point somewhere in region R. The cost function can be written as where is the center vertex, is the cost of the optimal path from there to the goal, and is the cost-per-distance in the region.

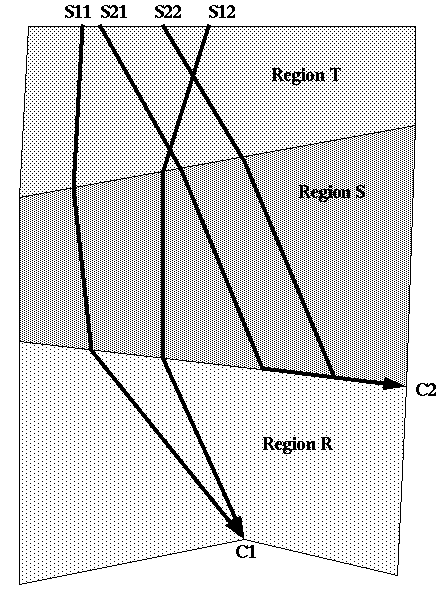
Figure 3: Example situations for the three kinds of cost-to-goal functions.

Optimal paths within a weighted region may not converge directly to a vertex, but may cut across to an adjoining lower-cost region and follow along its edge to the end vertex (a "reflection wedge"). This situation occurs with cross-country travel when it is easier to head for a nearby road rather than straight toward a goal. Fig. 3 shows an example of two optimal paths from S21 and S22 travelling through region S to the boundary of lower-cost region R, then following along the boundary to converging point C2. Then the cost surface is a tilted plane in the region before the edge following (region S of Fig. 3) . This is since all optimal paths there must be parallel to achieve the critical "internal reflection" turn angle of with the edge to obey Snell's Law, where is the cost per distance in the high-cost region and in the low-cost (edge-following) region. In a coordinate system where the edge is horizontal and the converging vertex (edge endpoint) is , the cost surface is:

where is the cost to the goal from the converging vertex.

If paths cross other weighted-region edges before reaching such a converging edge, the cost surface is planar in the earlier regions too (for instance, in region T for the paths S21 to C2 and S22 to C2 in Fig. 3). This is because all optimal paths in the earlier regions must be parallel too, since Snell's Law requires that the heading in an earlier region be a function of the heading in the subsequent region; and because the optimal cost to the goal anywhere along an intermediate weighted-region boundary must be a linear function of distance along the boundary, since the intersection of a tilted plane for the cost function with a vertical plane representing the boundary must be a straight line. The exact plane can be fit by tracing any two optimal paths through the area of interest and calculating cost-to-goal at three places.

Finally, if paths in a WBPS cross one or more weighted-region edges before converging directly on a vertex rather than along a line, the cost surface in each of the regions except the last is an asymmetric distortion of a cone (and a perfect cone in the last region). An example is the cost in region S for paths like S11 to C1 and S12 to C1 in Fig. 3. These "distorted cones" asymptotically approximate cones away from their central vertex. The distortion is to the direction of the gradient vector on the cone surface, and is analogous to what happens to light rays in a poor optical lens. Mathematically, the surface can only be expressed parametrically [Alexander and Rowe 1990].

However, an exact cone can often fit the surface well since the surface must be smooth (cost-to-goal cannot change abruptly) and WBPSs are often narrow. Consider the cost surface in the weighted region across a single edge from a vertex to which all paths converge. Use a Cartesian coordinate system in which the region edge coincides with the x-axis, and the y-axis is the line through the converging vertex that is perpendicular to the edge. Let be the cost-per-distance in the distorted-cone region, in the perfect-cone region; h the distance of the converging vertex from the edge; the angle the optimal path from (x,y) makes with respect to vertical to the edge in the distorted-cone region; and the angle with respect to vertical that same path makes in the converging-vertex region. Then paths in the distorted-cone region near this path appear to converge on a virtual cone center at a distance from the edge of where is the x-coordinate of the edge crossing, which simplifies to . So the center of this distorted cone is at and , with an inferred cost at that virtual-cone center of where is the cost to the goal from the actual converging vertex. This says the virtual cone center is always on the converging-vertex side of the edge. When , the virtual center is close to the edge and more distortion occurs; when , the virtual center is farther from the edge, the surface approaches a plane with less distortion.

The cost surface for paths that cross two or more weighted-region boundaries before converging to a vertex (like for region T and the paths S11 to C1 and S12 to C1 in Fig. 3) can be obtained by computing the virtual-cone center at each boundary in succession backward from the convergence point. The radius to the distorted-cone center replaces that to the exact-cone center in the above calculation. Distortions of the cone are typically less with each boundary, since the virtual cone radius usually increases and hence the surface approaches a plane. The radius usually increases because the paths have further to travel to the goal, and a consistently strong "focusing" effect is necessary to counteract this. WBPSs tend to narrow anyway as they cross region boundaries because they often get partitioned there as explained in section 4.3.

How good is the approximation of a distorted cone by an ideal cone? We conducted representative experiments. Fig. 4 shows the relative cost error of an exact-cone approximation of the cost surface for optimal paths that cross two weighted-region boundaries before converging on a vertex, like the paths S11-C1 and S12-C1 in region T of Fig. 3. We assume that the converging vertex is 1 unit from the lower boundary, and that the cost rate in its region is 1; we also assume the lower boundary is the line y=0. The horizontal axis of the graphs is the average rate of cost change per unit distance along the lower boundary, the best predictor parameter that we found. The top graph shows the maximum error and the bottom graph the mean error. In each graph, the top curve is for start points on the edge of the top region (the region furthest from the converging vertex), the middle curve for start points 1 unit into the top region, and the bottom curve for start points 10 units into the top region. Fig. 4 was obtained from 21,198 data points covering a five-dimensional space defined by the starting heading, the cost rates in the top and middle regions, and two parameters describing the top-region boundary line. The starting headings tested were 0.037 radians apart; cost rates ranged from 0.2 to 5; the boundary-line y-intercept from 0.1 to 10; and the boundary heading from -1.5 to 1.5. Although our experiments covered a wide variety of situations including some extreme ones, the graphs demonstrate that the error is to some extent predictable, and the mean error is quite small. The few situations of large errors (for headings near the critical heading for a nearby boundary) can be eliminated by subdividing WBPSs lengthwise.

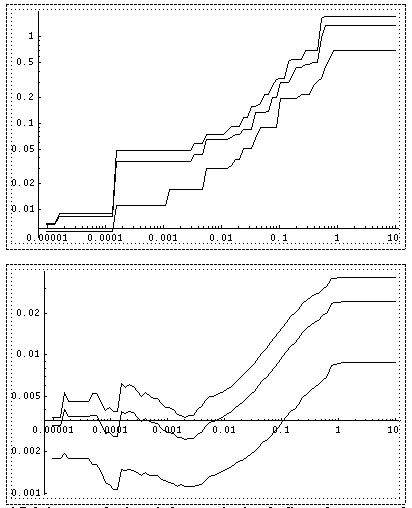
Figure 4: Relative error of estimate in the approximation of a distorted-cone cost surface by an exact-cone surface for optimal paths crossing two weighted-region boundaries before converging on a vertex. See the text for assumptions made. The horizontal axis is the absolute value of the rate of change of the cost of the optimal path to the converging vertex per unit distance along the further boundary where the test path crosses it. The top graph shows maximum error and the bottom shows mean error. On each graph, the top curve represents the error along the further boundary, the middle curve the error for paths that start one unit from the boundary on the side away from the converging vertex, and the bottom curve the error for paths that start ten units from the boundary.

Intersections of cost surfaces

Behavioral boundaries become easier to understand when related to intersections of three-dimensional optimal-cost surfaces. When two WBPSs overlap in the map plane, the resulting optimal-cost surface is the minimum of their two surfaces. Thus the projections to the map plane of where those surfaces intersect represent behavioral boundaries for optimal paths, across which the optimal WBPS changes. To find the boundaries we must thus intersect cones, planes, and distorted cones. Note that intra-wedge behavioral boundaries only appear where the two associated WBPSs overlap. If a calculated behavioral boundary lies entirely outside the region of overlap, one WBPS is always optimal in that region.

Hyperbola boundaries occur when two cone cost surfaces intersect. This happens when , where is the cost rate for the region in which the boundary occurs, and are the map-plane distances of a behavioral-boundary point from the center points of the two cones, and and are the costs from each cone center to the goal. Thus the boundary is the locus such that is a fixed constant of , one definition of a hyperbola.

Parabola boundaries occur when a cone cost surface intersects a plane cost surface. This happens in the simplest case when , where is the distance to a converging edge for the plane, is the distance along the edge, is the cost rate of the region in question, is the cost of the lower-cost outside region, and is the cost from the converging point on the edge to the goal point. Thus for the behavioral boundary, is a fixed constant . But is just the distance from the edge to the projection of the converging point on the line of the path. Hence is the total distance to a directrix through the plane's defining point at an angle of away from the boundary. Hence the boundary is the locus of points equidistant from a point and a line, a parabola.

Linear boundaries occur when two plane cost surfaces intersect, and for all weighted-region boundaries by definition. They also occur for adjacent wedges separated by an optimal path. "Adjacent" means that they represent contiguous ranges of headings at the goal point and all other defining points for each wedge. Since optimal paths are piecewise-linear, these behavioral boundaries are piecewise-linear.

Distorted hyperbolae and parabolae occur when distorted cones intersect other surfaces. If the distorted cone approximates an ideal cone with an error of E, its behavioral boundaries in a region with cost rate will lie within distance of the exact-cone boundaries. [Alexander and Rowe 1990] showed that behavioral boundaries were most curved near a start or converging point, and that it is best to approximate the cone on its side of greatest curvature. With more significant errors, as for a wide WBPS, accuracy can be improved by partitioning the WBPS lengthwise by ray-tracing paths equally spaced within it. Fig. 4 provides guidance as to the approximation accuracy. Our experience with implementation of the algorithm has been that error is usually negligible.

Partitioning of path subspaces about vertices

Now we must explain the algorithm by which WBPS wedges and behavioral boundaries are found. We will follow our fixed-start fixed-goal algorithm [Rowe and Richbourg 1990] with behavioral-boundary calculations attached in certain circumstances. The algorithm uses A* search to recursively partition path subspaces about terrain vertices until the wedges are all sufficiently narrow to be WBPSs. The main loop splits a wedge into left, right, middle, and reflection subwedges (or path subspaces) associated with a weighted-region or critical-angle (explained below) vertex V within the wedge. At each step in an A* heuristic search, we choose the unexamined V closest in cost to the goal and split it.

More specifically, to split a wedge we first find the optimal path backward from the goal to the chosen vertex V. Then we ray-trace V's "left-grazing path" from the goal, the optimal path that passes just left of V. Such paths may just continue straight if V is a left corner of a region, or they may be refracted according to Snell's Law (like the paths V1 to SL1, V2 to SL2, V3 to SL3, and V4 to SL4 in Fig. 5) if a weighted-region edge extends from V to the left. Continue tracing the left-grazing path as far as possible; if Snell's Law does not permit a continuation across some edge encountered, the path terminates there. Define the "left subwedge" now as a wedge whose left side is the original left side, and whose right side is followed by the left-grazing path from V.

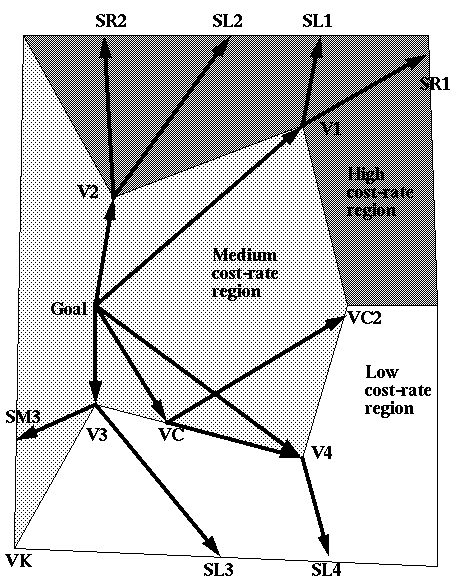
Figure 5: Cases for partition of wedges into subwedges at vertices. (Arrows are the reverse of path direction because analysis proceeds backward from the goal.)

An analogous method can find the right-grazing path and the right subwedge at vertex V. Fig. 5 shows right-grazing paths for V1 to SR1 and V2 to SR2. (V3 and V4 in Fig. 5 have no right-grazing paths because Snell's Law does not permit entering the low-cost region for such shallow angles of incidence.) If the left-grazing path does not cross the right-grazing path, a "middle subwedge" is created between the left subwedge and the right subwedge, a subspace of paths that follow to V and then travel off at headings between those of the left-grazing and right-grazing paths (except where such paths would enter an untraversable obstacle). Vertex V is a converging point for this middle wedge, and has a perfect-cone cost surface near V. Vertex V1 in Fig. 5 has a middle wedge for paths between SL1 and SR1. But there is no middle wedge if the left-grazing path crosses the right-grazing path, like at vertex V2 in Fig. 5; then the left and right subwedges overlap in the high-cost region and create a behavioral boundary extending away from the vertex in a distorted hyperbola.

Another kind of middle subwedge is a "reflection middle subwedge". These are wedges that follow to V, follow along the lower-cost side of a weighted-region edge emanating from V, and then cut into the higher-cost region at the critical reflection angle (defined in section 4.1) for that edge, so that the edge functions like a low-cost "road" and the criteria of [Rowe 1990] apply. Paths through V3 in Fig. 5 can do this along the edge V3-VK; the reflection wedge is bordered above by the path V3 to SM3. Such wedges have a plane cost surface in the higher-cost region. Such a reflection wedge can overlap another reflection wedge at the same vertex V coming from the opposite side of a high-cost region (creating a straight-line behavioral boundary bisecting the two edges). But some reflection wedges and their behavioral boundaries are ruled out by the following theorem.

Theorem 4.1: Optimal paths from S through weighted-region vertex V that follow a weighted-region edge E away from V and then refract across E at its critical angle can only occur if E is not reachable by either the left-grazing or right-grazing paths about V; and that behavior is always then better than following to V and then travelling straight in the high-cost region. Proof: Assume that such a reflection path follows an edge E reachable by the right-grazing path (the argument is analogous for left grazing). The right-grazing path, obeying Snell's Law across all edges, must reach points on E infinitesimally close to V at a lower cost than going through V since Snell's Law gives a concave local optimum within a WBPS [Rowe and Richbourg 1990]; and we can always pick a path close enough to V to be guaranteed a WBPS between it and if V is the closest unexamined vertex to S. Hence the first part of the theorem follows. To prove the second part, let the cost-per-distances of the two regions along edge E be and , , and the lengths of the two parts of the reflection-wedge path from V to some I in the high-cost region be and ; then the reflection wedge provides a better route to I than the middle wedge if:

which simplifies to, which must always be true. QED.

Another kind of reflection wedge can start from the middle of an edge. These represent paths that reach an edge from a higher-cost region, follow along the edge on the lower-cost side, and then cut back into the higher-cost region; both turns must be of the critical reflection angle. Fig. 5 gives an example for paths from the goal to VC at the critical angle, which can then follow along the VC-V4 edge any distance before cutting back into the medium-cost region at the critical angle; this wedge is bordered by the path VC to VC2. Such wedges can be found for each edge of a lower-cost region in turn by iterative ray tracing from the start point of a wedge, looking for starting angles such that the path meets the edge at the critical angle; the place where the path so meets the edge is the converging point for the wedge, and [Rowe and Richbourg 1990] proves there is only one such vertex. Since finding such a vertex is analogous to finding the optimal path to a weighted-region vertex, both can be done within the same A* search, where the nearest vertex in cost of either kind should be chosen next to work on. Note that such a reflection wedge must always overlap itself, and this creates a behavioral boundary extending from its converging point that is either a line, a parabola, or a distorted parabola.

Examples

Fig. 6 shows behavioral boundaries created by our algorithm implementation for a quadrilateral weighted region (shaded) of twice the cost-per-distance of its surroundings with a goal point beneath the quadrilateral. The numbers represent behavioral regions, and the arrows approximate the optimal path direction to the goal for each region. (All paths in region 9 head directly at the goal.) Fig. 7 is the optimal-path tree for the behavioral regions of Fig. 6; each path to the tree root represents a WBPS. For instance, there is a WBPS for start points in region 3, whose optimal paths travel north-northwest to the edge of region 6, then turn left sixty degrees to follow the region-6 side of the edge to the upper left corner of the quadrilateral, then follow the region-8 side of the quadrilateral down to its lower right corner, and then head to the goal through region 9.

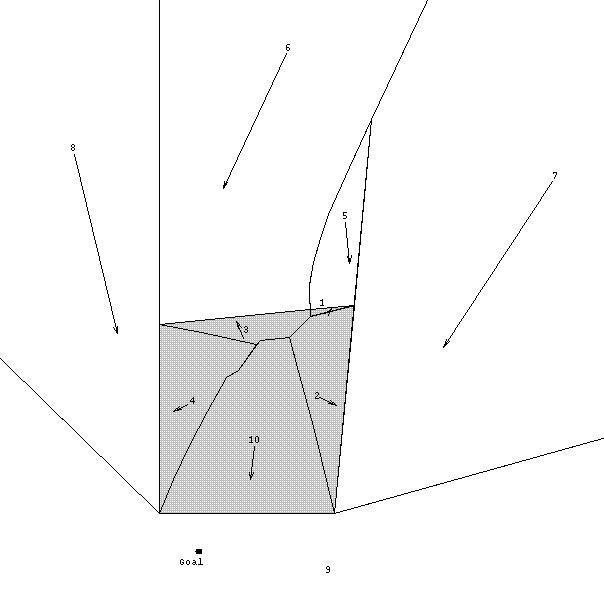
Figure 6: An example optimal-path map resulting from the wedge-partition algorithm on terrain with a single quadrilateral area (shaded) of twice the cost-per-distance of its surroundings. The goal point is on the bottom; the other lines are behavioral boundaries, the numbers indicate behavioral regions, and arrows indicate the approximate optimal direction for paths within the behavioral region.

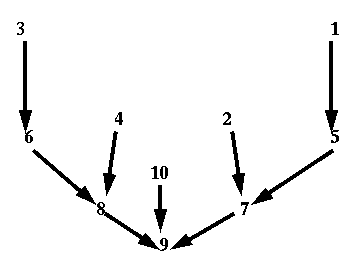
Figure 7: The optimal-path tree for the behavioral regions in Fig. 6; paths to the root correspond to WBPSs (well-behaved path subspaces).

The linear boundaries 8-9, 7-9, 6-8, 5-7, 4-8, 3-6, 1-5, and 2-7 in Fig. 6 are created by optimal paths between adjacent wedges. The linear boundaries 3-4, 2-3, 1-2, and 1-3 are created by intersections of plane surfaces of reflection wedges. The boundary for 5-6 and 5-7 is a true hyperbola, created by intersecting cone surfaces for paths that go around the quadrilateral clockwise and counterclockwise. The boundaries 4-10, 3-10, and 2-10 are distorted parabolae, created when planes for three reflection wedges intersect the distorted cone surface for region 10; the center of the distorted cone for region 10 is below the goal near the framing line. The glitches in the boundaries 3-10 and 4-10 signal errors that could be eliminated by smoothing or subdividing the 10-9 wedge. This run took 634 seconds of CPU time using semi-compiled Quintus Prolog on a Sun-3 server, and used 925K of storage including the language interpreter. Much of the time was spent on computing line intersections since we used only a simple method.

Fig. 8 shows the results of the algorithm on terrain where the left polygon is an obstacle and the right polygon is a weighted region. (The Figure was drawn by the implementation, as was Fig. 6). The lower boundary of region 9 and the upper boundary of regions 8 and 7 are hyperbolae; the upper boundaries of regions 18 and 17 are distorted parabolae; and all other boundaries are straight. Fig. 8 required about an hour of CPU time.

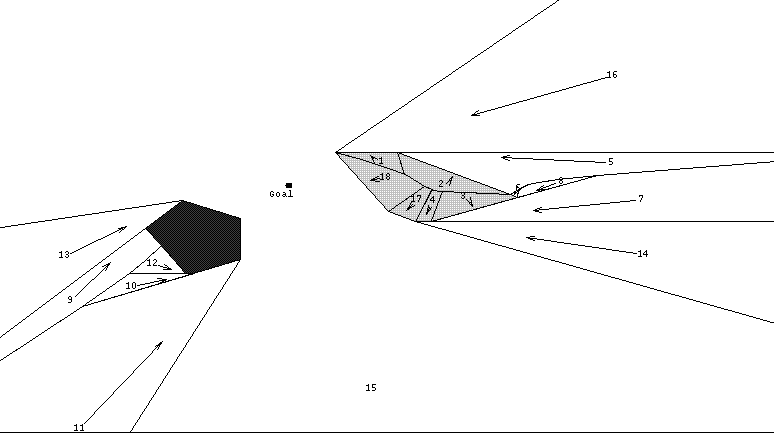
Figure 8: The final region boundaries found by the wedge-partition algorithm on terrain with an untraversable obstacle polygon on the left and a high-cost polygonal region (of twice the cost-per-distance as its surroundings) on the right; the goal point is between the two regions. Arrows represent approximate optimal-path directions, and the other lines represent behavioral boundaries.

Wedge-termination behavioral boundaries

Some behavioral boundaries in Fig. 8 (like 9-11, 2-18, and 5-7), and 3-10 in Fig. 6, involve overlaps of wedges not adjacent on the optimal-path tree, a generalization of the cases mentioned in section 4.3. Finding all such boundaries might seem to require checking every wedge pair. But these boundaries only can occur only where the wedges actually overlap in a weighted region, and only where all intermediate wedges in the optimal-path tree (those whose starting headings from the goal point lie between the starting headings of the overlapping wedges) terminate before the region of overlap. Termination can occur at an uncrossable edge or along a behavior boundary. For instance in Fig. 6, the wedge for region 4 terminates along behavioral boundaries with regions 10 and 3, permitting regions 10 and 3 to create their own behavioral boundary extending right from the intersection of the 3-4 and 4-10 boundaries. Note that since nonpath behavioral boundaries extend from intersections of other behavioral boundaries, all boundaries form a connected graph like the Delaunay triangulation dual for Voronoi diagrams.

To get the behavioral boundary when two arbitrary wedges overlap, cost surfaces can be computed following section 4.1, and the behavioral boundary found following section 4.2. If the boundary lies outside the region of overlap, one wedge is better than the other everywhere they overlap (and can be found by calculating the cost to a single point in the overlap), and the poorer wedge must be truncated where it starts the overlap. Otherwise, the behavioral boundary must be intersected with the region of overlap. Paths in the wedges that hit the boundary remainder terminate there. If the remainder comprises several pieces, analysis can be done separately on each piece, but this occurred very rarely in our experience.

Accuracy analysis

The following theorem answers a key question about the wedge-partition algorithm.

Theorem 4.2: The wedge-partition algorithm described above will obtain the optimal-path map to an arbitrary degree of accuracy provided the Snell's Law inversion is done to an arbitrary degree of accuracy and provided that all behavioral boundaries are accurate to an arbitrary degree of accuracy. Proof: The fixed-start fixed-goal weighted-region algorithm of [Mitchell and Papadimitriou 1991] is proved correct for an arbitrary degree of accuracy in the Snell's Law inversion. In the worst case, this algorithm finds optimal paths to every vertex in the area of interest, which is equivalent to finding optimal paths to the start point from every one of those vertices since a weighted-region path is reversible. Our algorithm above extends [Rowe and Richbourg 1990] (if we triangulate regions) to reason about all possible start points, not just weighted-region vertices. But for the algorithm to correctly terminate in the worst case, every wedge must be a WBPS, because the optimal path might be found in expansion of the very last non-WBPS wedge. Within a WBPS, all start points have the same locally optimal behavior to reach the goal. Hence, since the globally optimal behavior must be a locally optimal behavior, one of the WBPSs reaching an arbitrary point V must contain the globally optimum path to V.

So the problem is just to figure which WBPS provides the global optimum for a point V when more than one WBPS reaches V. This can be ensured by truncating suboptimal parts of WBPSs, as soon as possible after they are created, to ensure that no overlaps occur between any segments. The branch-and-bound aspect of the algorithm ensures this. With this, no wedge is extended past a segment until we are sure it has not been sliced by another wedge within that segment. Hence we will end up with non-overlapping behavioral regions that represent globally optimal behaviors. QED.

Complexity analysis

Our algorithm extends the single-start single-goal algorithms of [Rowe and Richbourg 1990] and [Mitchell and Papadimitriou 1991] by doing additional work. We can obtain a worst-case complexity for our algorithm by comparing it to [Mitchell and Papadimitriou 1991] and an average-case complexity by comparing it to [Rowe and Richbourg 1990].

Theorem 4.3: The worst-case preanalysis time of wedge-partition algorithm is , average-case is , worst-case execution time is , average-case execution time is , and preanalysis and execution-time space is , where v is the number of weighted-region vertices. Proof: Use of the map at execution time in the worst case requires effort for finding of the behavioral region a given start point is in, since there are edges, and time for adjustment of the path to the goal as per [Rowe and Richbourg 1990]. In the average case, however, the adjustment of the path to the goal can be adequately accomplished by a fixed number of iterations per edge as discussed in [Mitchell and Papadimitriou 1991], so average execution time is from the first step.

As for map-building (preanalysis) time, this is at least the complexity of [Rowe and Richbourg 1990] because in the worst case of the fixed-start fixed-goal problem, every optimal path to weighted-region vertex must be found just as in constructing an optimal-path map, and the wedge-decomposition method is the same. ([Mitchell and Papadimitriou 1991] triangulates nonconvex regions, which can increase v.) Additional work is required, however, to compute wedge overlaps and behavioral boundaries. The final optimal-path tree contains WBPSs, since v partitions are done. Each wedge has segments, since there are edges and each edge can be crossed times on the same path, for total segments. The number of possible wedge-segment overlaps that must be considered is thus because adjoining wedges do not necessarily cross the same regions and we must, in the worst case, check a segment against all the other segments on the two neighbor wedges.

Then for each potential overlap, we must compute the behavioral boundary from the equations of the cost surfaces in the overlapping segments. The cost surface for each new segment can be computed as the wedge is expanded at just constant extra time per segment, and need only be represented by the cost on the endpoints of the last weighted-region boundary plus the focus or virtual focus, if any, as discussed in section 4.1. The computation of the behavioral boundary can be done in time independent of v using the methods of section 4.2, or perhaps even with decreased time as v increases since more terrain vertices mean smaller regions and easier fitting of curves. Then the boundary must be intersected with the two overlapping wedge segments, requiring intersection checks. In the worst case, the boundary will intersect both segments, so an operation must traverse the boundaries of the segments to construct the truncated segments, as discussed in section 4.5. Hence there are operations for each pair of overlapping wedges. Hence there are operations to build the optimal-path map in addition to the wedge decompositions. But the wedge decomposition process itself is . Hence that remains the worst-case complexity of the problem of building an optimal-path map.

In the average case, [Rowe and Richbourg 1990] shows an algorithm similar to [Mitchell and Papadimitriou 1991] that has complexity in the average case for the fixed-start fixed-goal problem. In that paper, the tree of wedges on the average is because each of the wedges consists on the average of segments. There are then checks for possible segment intersections, and each requires checks for intersection with the boundaries. Hence the average-case complexity of our optimal-path algorithm .

The space required for map building must hold wedges of segments, following the space analysis in Theorem 2.1. Each segment requires a description of previous region of space, a cost function for the segment of space, and a description of its polygonal boundary. The latter requires space because segment polygons before overlap have four vertices, and each overlap and truncation adds points to the boundary, following the previous discussion, and there are possible overlaps for a given segment. Hence preanalysis space is . At execution time, we can eliminate the cost function information from the storage space, but everything else is still required, so the space remains . QED.

Note that despite the above worst-case results, a big advantage of our wedge-partition approach to optimal-path maps is in its reduced final storage requirements in the average case. Only behavioral boundaries need be stored, and only a few parameters describe each behavioral boundary within a weighted region. The parameters stored for wedge partition also simplify the task of finding the optimal behavior using an optimal-path map: One need only calculate on what side of a near-quadratic curve your position lies rather than checking against a list of points as with the other algorithms. Since the amount of detail stored can vary over the terrain, redundant data is eliminated with our approach unlike with wavefront-propagation methods. At the same time, our algorithm improves upon the space required by path-caching methods because it represents an informed way to find the paths most critical in defining an optimal-path map. The reduced storage requirements of our algorithm speed the use of the optimal-path map; the degree of speedup depends on the terrain, but speedups on the order of 10 were achieved in our experiments.

Implementation issues

Our actual implementation uses bounding rectangles around behavioral regions to quickly test whether two regions can overlap. Anytime a new region is discovered not to contain any terrain vertices, its bounding rectangle is checked for overlap with bounding rectangles of other behavioral regions; if an intersection is found, the actual overlap is computed. This improves average performance at the expense of worst-case performance.

The implementation does several things to get accurate behavioral boundaries. When overlapping wedges are found, it first computes the region of overlap, and then fits cost surfaces within it. This gives very accurate approximations for distorted cones in small areas of overlap. (The overlap calculation is complex, because the regions are often nonconvex and require many-sided polygons to model accurately after being sliced by curved boundaries). When new behavioral regions are created, it immediately tries to merge them into adjacent regions with the same behavior. Finally, it caches records of all behavioral-region pairs found to be nonoverlapping although their bounding rectangles overlap; and when such behavioral regions are subdivided, we can infer the subpieces do not overlap.

Conclusions

We have provided the first general algorithm for constructing optimal-path maps to a controllable degree of accuracy for the weighted-region path-planning problem. Such maps specify the best route to a goal point from anywhere in two-dimensional weighted-region terrain. Good ways to build them address the complaint that finding optimal paths takes too much time to be useful in the real world: Map construction can be done long in advance and map use can be fast. Our approach is to compute a cost-to-goal function for everywhere in a terrain area, and then its gradient indicates the direction of the optimal path everywhere. Our wedge partition algorithm is slower than its two main competitors (see Fig. 1) but its results are more accurate and generally require less storage space. Our algorithm should be desirable when much planning time is available (as for daily routes of a sentry robot), when high accuracy is needed (as for indoor emergency paths or for lens-system design), or for evaluating the accuracy of other path-planning methods (as for deciding whether potential fields produce paths sufficiently close to optimum for an application). The next steps should be further testing of the algorithm on real-world terrain, and development of methods for updating maps when the terrain changes.

References

Alexander, R. S. 1989 (September). Construction of optimal-path maps for homogeneous-cost-region path-planning problems. Ph.D. thesis, Dept. of Computer Science, U.S. Naval Postgraduate School, Monterey, CA , USA.

Alexander, R. S. and Rowe, N. C. 1990 (May). Path planning by optimal-path-map construction for homogeneous-cost two-dimensional regions. Proceedings of IEEE International Conference on Robotics and Automation, Cincinnati, OH, pp. 1924-1929.

Chen, D. Z., Klenk, K. S., and Tu, H.-Y. T. 1995. Shortest path queries among weighted obstacles in the rectilinear plane. Proceedings of the 11th Annual ACM Symposium on Computational Geometry, Vancouver, BC, Canada, pp. 370-379.

Chew, L. P. and Drysdale, R. L. 1985 (June). Voronoi diagrams based on convex distance functions. ACM Symposium on Computational Geometry, Baltimore, Maryland, pp. 235-244.

Hershberger, J. and Suri, S. 1993. On computing euclidean shortest paths in the plane. Proceedings of the 34th Annual IEEE Symposium on the Foundation of Computer Science (FOCS 93).

Hwang, Y. K. and Ahuja, N. 1992 (September). Gross motion planning--a survey. ACM Computing Surveys, 24, 3, pp. 219-291.

Kambhampati, S. and Davis, L. S. 1986. Multiresolution path planning for mobile robots. IEEE Journal Of Robotics And Automation RA-2: 3, September 1986, pp. 135-145.

Lee, D. T. and Drysdale, R. L. 1981 (February). Generalization of Voronoi diagrams in the plane. SIAM Journal on Computing, 10, 1, pp. 73-87.

Lee, D. T. and Preparata, F. P. 1984. Euclidean shortest paths in the presence of rectilinear barriers. Networks, 14, pp. 393-410.

Mitchell, J. S. B., Payton, D. W., and Keirsey, D. M. 1986. Planning and reasoning for autonomous vehicle control. International Journal of Intelligent Systems, 11, 129-198.

Mitchell, J. S. B. and Papadimitriou, C. H. 1991 (January). The weighted region problem: finding shortest paths through a weighted planar subdivision. Journal of the Association for Computing Machinery, 38: 1, 18-73.

Mitchell, J. S. B. 1988. An algorithmic approach to some problems in terrain navigation. Artificial Intelligence, 37, 171-201.

Mitchell, J. S. B. 1993 (May). Shortest paths among obstacles in the plane. Proceedings of the Ninth Annual ACM Symposium on Computational Geometry, pp. 308-317.

Mobasseri, B. G. 1990 (November). Impact of uncertain terrain models on the weighted region problem. Proceedings of Mobile Robots V, SPIE (The International Society for Optical Engineering), volume 1388, Boston MA, USA, pp. 269-277.

Nilsson, N. 1980. Principles of artificial intelligence. Palo Alto, CA: Tioga.

Parodi, A. M. 1985. Multi-goal real-time global path planning for an autonomous land vehicle using a high-speed graph search processor. Proceedings of the 1985 IEEE Conference on Robotics and Automation. New York: IEEE Press, pp. 161-167.

Payton, D. W. and Bihari, T. E. 1991 (August). Intelligent real-time control of robotic vehicles. Communications of the ACM, 34, 8, pp. 48-63.

Reif, J. H. and Storer, J. A. 1994. Shortest paths in the plane with polyhedral obstacles. Journal of the ACM, 41, 5, pp. 982-1012.

Rowe, N. C. 1990 (December). Roads, rivers, and obstacles: optimal two-dimensional route planning around linear features for a mobile agent. International Journal of Robotics Research, 9, 6, pp. 67-74.

Rowe, N. C. and Alexander, R. S. Path planning across weighted regions using optimal-path maps. Technical report, U. S. Naval Postgraduate School, January 1997.

Rowe, N. C. and Richbourg, R. F. 1990 (December). An efficient Snell's-law method for optimal-path planning across multiple homogeneous-cost regions. International Journal of Robotics Research, 9(6), pp. 48-66.

Schoppers, M. J. 1989 (Winter). In defense of reaction plans as caches. AI Magazine, 10, 4, pp. 51-60.

Go to paper index