I

NAVAL POSTGRADUATE SCHOOL

Monterey, California

THESIS

Approved for public release; distribution is unlimited.

STATIC-TASK SCHEDULING INCORPORATING PRECEDENCE CONSTRAINTS AND DEADLINES IN A HETEROGENEOUS-COMPUTING ENVIRONMENT

Michael D. Niedert-Lieutenant, United States Navy

B.S., United States Naval Academy, 1990

Master of Science in Computer Science-June 2000

Advisor: Neil Rowe, Department of Computer Science

Second Reader: CDR Deborah Kern, Department of Computer Science

Distributed systems have grown in popularity due to the rapid increase in networking of personal computers. A mixture of computers consisting of different architectures can be more powerful, reliable, and scalable than a single supercomputer. The problem of optimally scheduling jobs on a cluster of heterogeneous machines to minimize the time at which the last machine finishes is NP-complete. Nonetheless, the choice of a heuristic algorithm greatly affects the speed of solution. This work evaluates a greedy algorithm, an A* algorithm, and a simulated annealing algorithm applied to the heterogeneous scheduling problem with deadline and dependency constraints. Tradeoffs of speed and schedule quality were noted between the algorithms. The greedy algorithm produced results quicker than the A* and simulated annealing algorithms, but with a lower schedule quality. Because of these offsetting performance criteria, an analysis was conducted to determine which algorithms should be used for which input cases.

DoD KEY TECHNOLOGY AREA: Computing and Software

KEYWORDS: Scheduling, Algorithms, Artificial Intelligence, Distributed Computing

REPORT DOCUMENTATION PAGE				Form Approved OMB No. 0704-0188
Public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instruction, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing this burden, to Washington headquarters Services, Directorate for Information Operations and Reports, 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302, and to the Office of Management and Budget, Paperwork Reduction Project (0704-0188) Washington DC 20503.
1. AGENCY USE ONLY (Leave blank)		2. REPORT DATE June 2000		3. REPORT TYPE AND DATES COVERED Master?s Thesis
TITLE AND SUBTITLE : Static-Task Scheduling Incorporating Precedence Constraints and Deadlines in a Heterogeneous-Computing Environment				5. FUNDING NUMBERS
6. AUTHOR(S) MICHAEL D. NIEDERT, LT, USN
7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES) Naval Postgraduate School Monterey, CA 93943-5000				8. PERFORMING ORGANIZATION REPORT NUMBER
9. SPONSORING / MONITORING AGENCY NAME(S) AND ADDRESS(ES) N/A				10. SPONSORING / MONITORING AGENCY REPORT NUMBER
11. SUPPLEMENTARY NOTES The views expressed in this thesis are those of the author and do not reflect the official policy or position of the Department of Defense or the U.S. Government.
12a. DISTRIBUTION / AVAILABILITY STATEMENT Approved for public release; distribution is unlimited.				12b. DISTRIBUTION CODE
ABSTRACT (maximum 200 words) Distributed systems have grown in popularity due to the rapid increase in networking of personal computers. A mixture of computers consisting of different architectures can be more powerful, reliable, and scalable than a single supercomputer. The problem of optimally scheduling jobs on a cluster of heterogeneous machines to minimize the time at which the last machine finishes is NP-complete. Nonetheless, the choice of a heuristic algorithm greatly affects the speed of solution. This work evaluates a greedy algorithm, an A* algorithm, and a simulated annealing algorithm applied to the heterogeneous scheduling problem with deadline and dependency constraints. Tradeoffs of speed and schedule quality were noted between the algorithms. The greedy algorithm produced results quicker than the A* and simulated annealing algorithms, but with a lower schedule quality. Because of these offsetting performance criteria, an analysis was conducted to determine which algorithms should be used for which input cases.
14. SUBJECT TERMS Scheduling, Artificial Intelligence, Distributed Computing					15. NUMBER OF PAGES
					16. PRICE CODE
17. SECURITY CLASSIFICATION OF REPORT Unclassified	18. SECURITY CLASSIFICATION OF THIS PAGE Unclassified		19. SECURITY CLASSIFICATION OF ABSTRACT Unclassified		20. LIMITATION OF ABSTRACT UL

NSN 7540-01-280-5500 Standard Form 298 (Rev. 2-89)

Prescribed by ANSI Std. 239-18

THIS PAGE INTENTIONALLY LEFT BLANK

Approved for public release; distribution is unlimited.

STATIC-TASK SCHEDULING INCORPORATING PRECEDENCE CONSTRAINTS AND DEADLINES IN A HETEROGENEOUS-COMPUTING ENVIRONMENT

Michael D. Niedert

LT, United States Navy

B.S., United States Naval Academy, 1990

Submitted in partial fulfillment of the

requirements for the degree of

MASTER OF SCIENCE IN COMPUTER SCIENCE

from the

NAVAL POSTGRADUATE SCHOOL

June 2000

Author: ___________________________________________

Michael D. Niedert

Approved by: ___________________________________________

Neil Rowe, Thesis Advisor

Approved by: ___________________________________________

Deborah Kern, Second Reader

Approved by: ___________________________________________

Dan Boger, Chairman, Computer Science

THIS PAGE INTENTIONALLY LEFT BLANK

ABSTRACT

Distributed systems have grown in popularity due to the rapid increase in networking of personal computers. A mixture of computers consisting of different architectures can be more powerful, reliable, and scalable than a single supercomputer. The problem of optimally scheduling jobs on a cluster of heterogeneous machines to minimize the time at which the last machine finishes is NP-complete. Nonetheless, the choice of a heuristic algorithm greatly affects the speed of solution. This work evaluates a greedy algorithm, an A* algorithm, and a simulated annealing algorithm applied to the heterogeneous scheduling problem with deadline and dependency constraints. Tradeoffs of speed and schedule quality were noted between the algorithms. The greedy algorithm produced results quicker than the A* and simulated annealing algorithms, but with a lower scheduler quality. Because of these offsetting performance criteria, an analysis was conducted to determine which algorithms should be used for which input cases.

THIS PAGE INTENTIONALLY LEFT BLANK

TABLE OF CONTENTS

I. INTRODUCTION *

II. PREVIOUS ATTEMPTS TO SOLVE THIS PROBLEM *

III. DESCRIPTION OF THE APPLICATION *

A. SMARTNET 7

B. MSHN 7

IV. DESCRIPTION OF THE PROGRAM *

A. NOTATION 11

B. THE SCHEDULING PROBLEM 13

C. GREEDY ALGORITHM 18

D. A* ALGORITHM 19

1. General Description 19

2. Cost Functions 20

3. Evaluation Functions 20

4. Data Structures 21

E. SIMULATED ANNEALING ALGORITHM 21

F. TEST SETUP 23

V. DISCUSSION OF RESULTS *

VI. CONCLUSION 29

APPENDIX A: TEXT OF THE PROGRAM 31

LIST OF REFERENCES 79

BIBLIOGRAPHY 81

INITIAL DISTRIBUTION LIST 83

THIS PAGE INTENTIONALLY LEFT BLANK

LIST OF FIGURES

Figure 1. MSHN Architecture. 9

Figure 2. A Directed Acyclic Graph (DAG) Representing a Task. *

Figure 3. Directed Acyclic Graph (DAG) in a Heterogeneous Environment. *

Figure 4. Multiple Schedules Satisfying the Same Directed Acyclic Graph (DAG). *

Figure 5. A Master Directed Acyclic Graph (DAG) representing Multiple Tasks. 17

THIS PAGE INTENTIONALLY LEFT BLANK

LIST OF TABLES

Table 1. Results of scheduling using a greedy algorithm, A* search algorithm,

and Simulated annealing algorithm with various precedence

constraints among jobs. 27

THIS PAGE INTENTIONALLY LEFT BLANK

I. INTRODUCTION

A distributed system is a collection of heterogeneous computers and processors connected via a network [GALLI00]. This collection works closely together to accomplish a common goal. The goal of a distributed operating system is to provide a common, consistent global view of the file system, name space, time, security, and access to resources. To provide this common view, there are numerous constraints and requirements on all participating systems; thus, distributed systems are generally referred to as tightly coupled systems.

Distributed systems have grown in popularity due to the rapid increase in personal-computer computing power per dollar. A mixture of computers with different architectures can be more powerful, reliable, and scalable than a single big supercomputer. A heterogeneous mixture of computers can be more powerful because of the sheer quantity of processors in the distributed system; it can be more reliable because failure of one computer does not result in failure of the system; and it can be more scalable because adding or removing computers from the system is easily accomplished.

To maximize performance in cluster environments, users can submit programs to a resource scheduling and management system that will execute them at the best location, returning the results to the user. Preferably, this management system will execute the application in a transparent manner; that is, the user will not know, except perhaps by getting better performance, that the application is not executed on the local machine. A scheduler for such a heterogeneous environment must be sophisticated. It must effectively schedule all of the jobs across the available machines, taking into account numerous factors, such as the deadlines of each job, the interdependencies among the jobs, and the heterogeneity of both jobs and machines.

Powerful, reliable, and scalable distributed systems have many applications in our current military. Examples of current military research in distributed systems are in real-time systems like telemedicine, video conferencing, distributed interactive simulations such as virtual battlefields, anti-ballistic missile systems, and communication systems.

The problem of optimally scheduling jobs on heterogeneous machines to minimize the time at which the last machine finishes is NP-complete. Nonetheless, the choice of a heuristic algorithm greatly affects the speed of solution. This work evaluates several approaches for the heterogeneous scheduling problem with deadline and dependency constraints. Specifically, three algorithms have been constructed and tested for the problem of scheduling jobs on a cluster of heterogeneous machines: a greedy algorithm, an A* search algorithm, and a simulated-annealing algorithm. The algorithms could be used by the Management System for Heterogeneous Network (MSHN) research program currently in progress at the Naval Postgraduate School.

PREVIOUS ATTEMPTS TO SOLVE THIS PROBLEM

A scheduling problem occurs whenever there is a choice as to the order in which tasks can be performed and/or in the assignment of tasks to servers for processing. A problem may involve jobs that need to be processed in a manufacturing plant, bank customers waiting to be served by tellers, aircraft waiting for landing clearances, or program tasks run on a parallel or distributed computer. There is a fundamental similarity to scheduling problems regardless of the difference in the nature of the tasks and the environment.

In the era of parallel and distributed computing, scheduling has started to gain the attention of many researchers. A program can be viewed as a collection of tasks which may run serially or in parallel. The goal of scheduling a set of tasks is to determine an assignment of tasks to processing elements and the times at which tasks are executed to optimize some performance measures.

If there are no precedence relations among the tasks forming a program, this problem is known as the task allocation problem [ALI94]. Task allocation has been studied extensively for the past two decades. The general problem of task scheduling is one of the most challenging problems in parallel and distributed computing. It is known to be NP-complete even in several restricted cases. Researchers have studied restricted forms of the problem by constraining either the task graph or the computer model. These cases can be solved efficiently, but are too far from real-world applications. To solve the problem in the general case, a number of heuristics have been introduced. These heuristics do not guarantee an optimal solution to the problem, but they try to find near-optimal solutions most of the time.

The scheduling investigated in this thesis is static scheduling, the assignment of tasks to processors before program execution begins. Static scheduling methods are nonpreemptive, meaning that once a job has begun execution, it cannot be interrupted. The goal of static scheduling is to minimize the overall execution time of a given set of tasks. Work on static scheduling methods by other researchers has attempted to [HURSON95]:

Predict the program execution behavior at compile time;

Group smaller tasks into coarser-grain processes to reduce the communication costs; and

Allocate processes to processors.

My work continues with this research, concentrating on the first and third of the bulleted items above.

Static scheduling can be either optimal or suboptimal [HURSON95]. One of the most critical shortcomings of static scheduling is that generating optimal schedules has been proven, even for it, to be NP-complete except in restricted cases (for example, when the execution time of all tasks is the same and only two processors are used). So most of the research and development has been focused on suboptimal solutions. These methods are classified into exact and heuristic suboptimal approaches. In heuristic methods, the solution space is searched in either a depth-first or a breadth-first fashion and the algorithm stops when a "good" (or acceptable) solution is reached.

The algorithms I present in this thesis illustrate both the exact and heuristic approaches. The "greedy" algorithm I implement uses a heuristic approach: A higher priority in the scheduling of tasks is given to those that have the smallest estimated computation time. The rule of thumb is that by scheduling a task on a machine with a smaller than average estimated time, we map the tasks to the machines which execute them most efficiently. In contrast, the A* algorithm I implemented uses an exact approach: Utilizing both a cost function which measures the actual time expended along a path, and an evaluation function which is an estimate of the time from any state to a goal, it is possible to find the quickest path to a goal whenever it exists. In order to take advantage of both the speed that heuristic approaches provide and the thoroughness that exact approaches provide, the simulated annealing algorithm I implemented uses the A* algorithm as a base and adds some random heuristics to enhance performance. The heuristics will cause the search to explore additional parts of the search graph which may result in finding a goal to the path quicker than the A* algorithm did.

Static scheduling suffers from a wide number of additional problems, most notably [HURSON95]:

The lack of efficient and accurate methods for estimating task execution times and communication delays can cause unpredictable performance degradations. Compile-time estimation of the execution time of a program?s tasks is often difficult due to conditions or iteration counts that are unknown before execution.

Existing task scheduling methods often ignore that data can be geographically distributed. This omission causes performance degradations due to run-time communication delays for accessing data at remote sites.

Static scheduling schemes need a tool to provide a performance profile of the predicted execution of the scheduled program on a given architecture. The user can then utilize this tool to improve the schedule or to experiment with a different architecture.

Although my thesis does not address these problems, they are areas researchers are currently studying. Several students and faculty performing research on the Management System for Heterogeneous Network (MSHN) have done research on these topics; they are critical to the success of the scheduling component of MSHN. Armstrong, Hensgen, and Kidd investigated estimation of task execution times, and discussed the relative performance of various mapping algorithms [ARMSTRONG98]. Bhat, Raghavendra, and Prasanna investigated various aspects of communication delays and their effect on performance in a distributed system [BHAT99]. Alhusani, Prasanna, and Raghavendra investigated a unified resource scheduling framework for heterogeneous computing environments [ALHUSAINI99]. Similar work was done with MSHN [FREUND98],[KIDD96].

DESCRIPTION OF THE APPLICATION

SMARTNET

The research which led to the current MSHN project originated with the SmartNet project. SmartNet was a scheduling framework for heterogeneous computing. Several research groups contributed to its development: NCCOSC RDTE Division in San Diego, SAIC, the University of Cincinnati, and the Naval Postgraduate School. SmartNet was different than other scheduling frameworks. Most frameworks use policies that employ Opportunistic Load Balancing (OLB). SmartNet, however, took into account not only the loads on various machines, but also, the performance of the application on various platforms (heterogeneity) [MSHN00].

The scheduling engine of SmartNet employed several scheduling algorithms. Two algorithms, "gensked" and "metasked", took into account scheduling of jobs with precedence constraints. Gensked and metasked belong to a class of "generational" scheduling algorithms that schedule the jobs starting at the root of the directed acyclic graph of task precedences and schedule a task after all its predecessor tasks are scheduled. They both use static algorithms.
MSHN

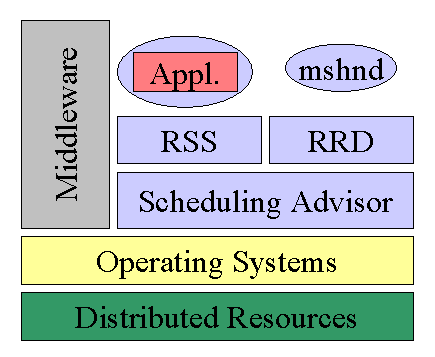
The MSHN project is an extension of the SmartNet research. The goal of MSHN is to develop a distributed system which will have naval shipboard applications. It is a part of the DARPA/ITO QUORUM program which is developing technologies that allow end users to achieve predictable and controllable end-to-end quality of service (QoS) for critical defense computing needs in a global heterogeneous distributed computing environment. The MSHN team is a collaboration between DoD (Naval Postgraduate School), academia (Naval Postgraduate School, University of Southern California, Purdue University), and industry (NOEMIX). The MSHN architecture will permit execution of multiple, disparate tasks that use a set of shared, heterogenous resources in a way that maximizes a collection of application-specific quality of service (QoS) measures. Factors influencing QoS for MSHN include security, deadlines, priority, adaptability (preferences for different versions), resource availability, and external users.

MSHN's components will perform several key functions. These include (1) monitoring general resource availability, (2) transparent sensing of resource requirements of applications, (3) on-line measurement of resource and system state, (4) mapping tasks and subtasks onto a heterogeneous suite of machines in a way that exploits heterogeneity, (5) adaptation of jobs to variations in the availability of resources, and (6) meeting QoS requirements including real-time deadlines, fault tolerance, security, and priorities. Because MSHN will be operating in an environment where usages and loads are not predictable, uncertainty will be quantified and accounted for in all of MSHN's components.

MSHN's architecture, shown in Figure 1, consists of (1) a client library that wraps system calls (including process-start requests), (2) a daemon (mshnd), (3) the Scheduling Advisor, (4) the Resource Requirements Database (RRD), and (5) the Resource Status Server (RSS). Users may submit jobs at any of the client sites. Process-start requests are sent to the Scheduling Advisor. The Scheduling Advisor queries the RRD for historical

Figure 1. MSHN Architecture.

and other information on the job, and also the RSS for information on status of resources. The Scheduling Advisor then determines the resources that are to be allocated for the job. The job is executed on these resources. Finally, the RRD and the RSS are updated. MSHN may use CORBA in its architecture, as well as integrating the above scheduling functions into an ORB (Object Request Broker) [MSHN00].

Scheduling is important to the MSHN project since it particularly addressed military applications and these generate scheduling problems. The detection and tracking of aircraft is a problem which needs efficient scheduling to ensure reliable performance of the system. Resources can?t be solely dedicated to detection, or solely dedicated to tracking one platform; scheduling must allow adequate allocation of resources such that each part of the air traffic control problem is satisfied. Or consider a naval ship which is required to detect, track, and target incoming missiles. Efficient scheduling is necessary to adequately allocate resources such that each part of the naval ship?s air defense mission is satisfied.

DESCRIPTION OF THE PROGRAM

NOTATION

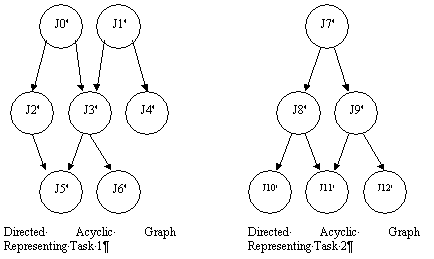
A task is a program or a set of programs to be executed upon a single request from a user. A task can consist of multiple jobs that can be distributed to multiple machines. Precedence constraints among jobs can be represented by ordered pairs of the form (Ji à Jj), which means that job Jj must not start executing before job Ji completes. Therefore, the precedence constraints define a partial order on the set of jobs that constitute a task. Hence, we can represent the tasks and precedence constraints by a Directed Acyclic Graph (DAG), which need not be a tree. We define the set of jobs that must complete before a job j can begin to be the Pred(j). Similarly, we define j to be a ready job if all of the jobs in Pred(j) have completed.

Figure 2 illustrates the above terms. A DAG representing a task consisting of 15 jobs is shown. The precedence constraints are shown by directed edges. Initially, Jobs J0, J1, and J2 are ready jobs. Jobs J3, J4, and J5 cannot be started until J0 completes. Similarly, Job J9 has to wait for both J3 and J4 to complete, before it becomes ready.

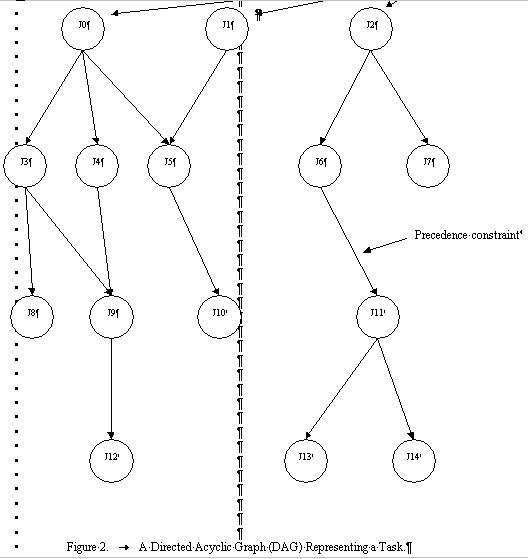
We now define an ETC matrix. ETC(j,m) is the expected time to complete job j on machine m, in a sterile environment. A sterile environment is one where no other jobs for the task use any other machines or the network connecting them.

A schedule is an assignment of the jobs to the available machines such that

the precedence constraints are not violated;
a job runs on exactly one machine;
a machine runs no more than one job at the same time; and
deadlines are met.

Figure 2. A Directed Acyclic Graph (DAG) Representing a Task.

The schedule will specify, for all jobs:

The machine on which the job should be executed;
The expected start time of the job on the selected machine; and
The expected completion time of the job on the selected machine.

THE SCHEDULING PROBLEM

The classic job scheduling problem is to determine an optimal schedule for a set of jobs and a set of machines, given precedence and deadline constraints, if any. For example, consider the DAG and the corresponding ETC matrix shown in Figure 3. Two different schedules are also shown in Figure 3 which satisfy this DAG. The DAG shows that job 2 and job 3 can start only after job 1 finishes. Similarly, job 4 can start only after both job 2 and job 3 finish, job 5 can start only after job 3 finishes, and job 6 can start only after both job 4 and job 5 finish. Its corresponding ETC matrix lists the ETC values of the jobs 1 through 6, for four different machines. For example, job 1 is expected to complete after 36 time units if it is executed on machine C, and job 3 after 41 time units if it is executed on machine A.

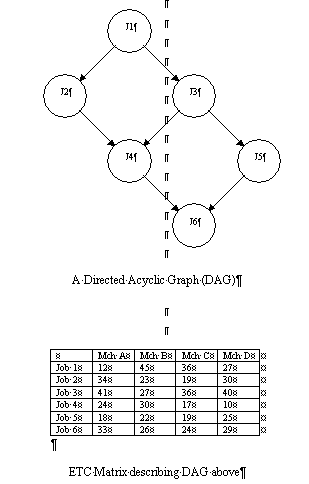
Figure 4 shows two example schedules for the DAG of Figure 3. Each row of the schedule depicts the execution of the machine corresponding to its label. Shaded boxes represent jobs. The job numbers are labeled. Empty boxes represent machine idle time. Schedule A has a length of 81 time units, and Schedule B, 90 time units. Schedule A is an optimal schedule. The best possible completion time will be bounded below by the time of the longest subsequence that starts at the root node of the DAG and ends at a leaf node. There are three sequences 1-2-4-6, 1-3-4-6, and 1-3-5-6 in this example DAG, having lengths 65, 73, and 81, respectively. The length of the longest path is 81. Hence, schedule A is an optimal schedule.

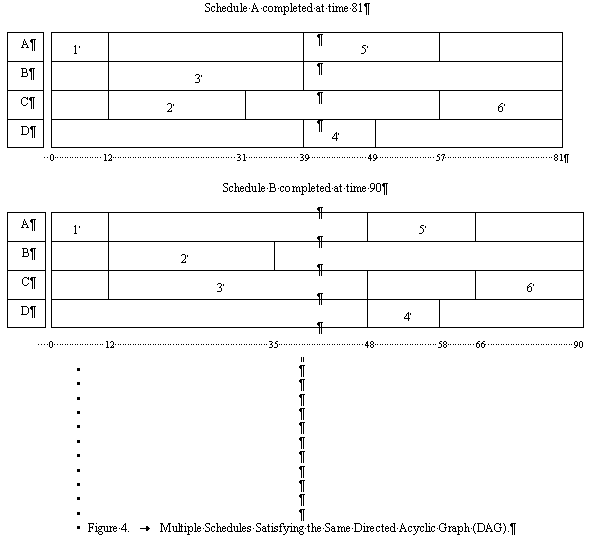
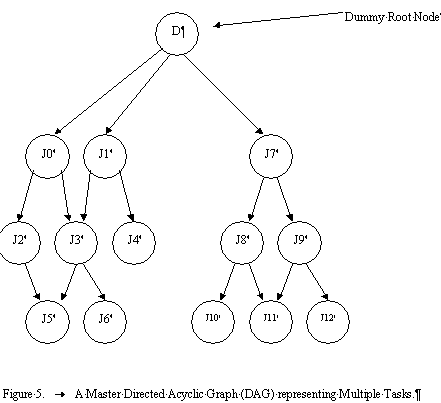
We note that machines can be idle in an optimal schedule, since there are precedence constraints among the jobs. We also note that if multiple tasks are submitted to the system, there will be multiple DAGs. However, throughout this thesis, we assume without loss of generality that there is only one DAG representing all the tasks since we can construct a master DAG which consists of a dummy root node and has the top level nodes of the DAGs representing the tasks as its children. See Figure 5

Each job is assumed to have a deadline, a time by which the job should be completed. The algorithms implemented use a "soft" deadline: If a job does not complete by its deadline, the system does not fail. However, each algorithm uses a cost function which penalizes missed deadlines. The more time from the deadline of the job to the start of the job, the higher the cost of the job. This relationship is linear.

It is useful to identify some additional assumptions made here.

These algorithms were tested in a linear heterogeneous environment where the ratio of the processing powers of any two machines is a constant. If two machines M1 and M2 are linearly heterogeneous, that means that one job running p times faster in machine M1 than in machine M2 implies that all jobs run p times faster in machine M1 than in machine M2.

These algorithms are for deterministic scheduling where it is assumed that complete information about the job to be scheduled is available prior to execution.

Figure 3. Directed Acyclic Graph (DAG) in a Heterogeneous Environment.

Figure 4. Multiple Schedules Satisfying the Same Directed Acyclic Graph (DAG).

Figure 5. A Master Directed Acyclic Graph (DAG) representing Multiple Tasks.

These algorithms are static scheduling algorithms. Scheduling algorithms can be classified based on the time at which scheduling decisions are made. In static scheduling algorithms, information regarding the entire task graph must be estimated prior to execution and all jobs are assigned to machines before any job starts execution.

These algorithms use non-preemptive scheduling, meaning that once a job has begun execution, it cannot be interrupted.

GREEDY ALGORITHM

A "greedy" algorithm was implemented to produce a schedule by a limited number of uncomplicated heuristics. Data structures used in the implementation of the algorithm were:

ETC[][]: A two-dimensional integer array is used to store the ETC values. As discussed, ETC(j,m) is the expected time to complete job j on machine m, assuming a sterile environment.

DEADLINES[]: A one-dimensional integer array is used to store the deadlines for each job.

DEPENDENCIES[][]: A two-dimensional integer array is used to represent precedence constraints among jobs. A "1" entered in the array represents precedence constraints between the i^thjob and the j^th job ? specifically, that job Jj must not start executing before job Ji completes. We say then that Ji is a parent of Jj, and Jj is a child of Ji.

CHECKSUM[]: A one-dimensional integer array is used to represent the current ability for a job to be scheduled without violating precedence constraints. Each index in the array corresponds to a job. The value stored represents the number of jobs currently required to be completed prior to the execution of that job. If the value is zero, then the job can be scheduled without violating any precedence constraints. Initial values are obtained by counting the nonzero values from the corresponding column of the dependency array. As jobs are scheduled, the array is updated to reflect current precedence constraints.

MACHINE_ETC[]: A one-dimensional integer array is used to represent the stop time of each machine, the time at which the machine will complete the job currently scheduled on it.

TASK_STATUS[]: A one-dimensional boolean array is used to represent the status of jobs scheduled, whether scheduled or not.

SCHEDULE_SUMMARY[][]: A two-dimensional array is used to store the results of the scheduling. The rows represent the jobs scheduled, and four columns give the job number, the machine that job was scheduled on, the start time of the job, and the completion time of the job.

The following steps are followed by the greedy algorithm.

Have all tasks been scheduled? If NO, continue with scheduling.

Look in the CHECKSUM array to determine all ready jobs, jobs that have no precedence constraints and can be scheduled.

Look in the TASK_STATUS array to determine which of these jobs have not been scheduled.

Find the minimum ETC value for each job which does not violate the corresponding job deadline in the DEADLINE array.

Select the minimum of these values over the jobs and identify the corresponding job and machine. Schedule this job on this machine.

Update the TASK_STATUS array to indicate the selected job has been scheduled.

Update the CHECKSUM array if the job scheduled was a parent of any other job remaining to be scheduled.

Repeat the above choices until all jobs have been scheduled.

The SCHEDULING_SUMMARY array will hold the final schedule.

A* ALGORITHM

General Description

The greedy algorithm discussed above is not guaranteed or designed to find the shortest schedule. This is desirable for our scheduling problem, as the main justification for distributed processing is speed. A heuristic that finds the minimum-cost path to a goal whenever it exists is said to be admissible [LUGER89]. One example of an admissible heuristic is that used by a restricted kind of breadth-first search, that explores in a level-by-level fashion. Since it looks at every state at level n of the graph before considering any state at the level n + 1, any goal nodes are found along the minimum-cost path provided that costs do not vary over branches.
Cost Functions

A cost function measures the work expended along a path between states. In our scheduling problem, the cost from the starting state (no jobs scheduled) to its descendants can be measured as total computing time. The cost of scheduling a specific job on a specific machine is simply the time it takes that job to execute on that machine. Then the cost of a state where multiple jobs are scheduled on multiple machines is the maximum of the individual machine completion times, or the time the last job completes.
Evaluation Functions

An evaluation function is an estimate of the cost from any state to a goal. In our scheduling problem, the cost from any state (where some jobs are scheduled) to the goal (where all jobs are scheduled) needs to incorporate the ETCs of the unscheduled jobs and the processing capabilities of the machines in the network. The best that could be accomplished at any given state would be to run all of the unscheduled jobs on the available machines with no idle time on any machine. To perform this calculation, we need the total estimated run time of all unscheduled jobs, and the total number of processors in the network. The estimated run time of an arbitrary unscheduled job is the mean of the estimated time to compute values over all machines for that job. The total estimated run time of all unscheduled jobs is the sum of the individual jobs estimated run times. The total number of processors in the network is known prior to scheduling. Therefore, to model all of the unscheduled jobs running on available machines with no idle time on any machine, we divide the total estimated run time of all unscheduled jobs by the total number of processors in the network. That total time could be used as a lower bound on the cost from any state to the goal. A* algorithms with a lower-bound evaluation function are admissible because they always find the optimal solution path as the first path to a goal. This is an important attribute for our scheduling problem, as we can use this as we compare results from A* to results of other algorithms.
Data Structures

Data structures used in the implementation of the algorithm are:

ETC[][]: A two-dimensional integer array is used to store the ETC values as with the greedy algorithm.

DEADLINES[]: A one-dimensional integer array is used to store the deadlines for each job as with the greedy algorithm.

DEPENDENCIES[][]: A two-dimensional integer array is used to represent precedence constraints among jobs as with the greedy algorithm.

agenda: A list representing all states visited that have not been evaluated for successor states or evaluated to be the goal state.

usedagenda: A list representing all states visited that have been evaluated for successor states and have been determined not to be the goal state.

SIMULATED ANNEALING ALGORITHM

The simulated annealing algorithm modifies the A* algorithm. In an A* search, the state chosen to be visited is the state with the lowest total cost plus evaluation function. In simulated annealing, that state has the highest probability of being chosen, but the other states are also possible with a probability. For example, if the first state in the sorted agenda had a total cost plus evaluation function of 20, and the second state had 21, the desirability of either state is virtually the same. However, if the first was 20, and the second was 50, the first should be definitely more desirable. So but the probability of choosing an item should depend on its total cost plus evaluation function relative to the first item in the agenda. The reason simulated annealing might perform better is that an A* search might start on a part of the search graph that looks promising, but is not a good path to the goal at all, and we don?t know that until we wasted valuable computation time. With simulated annealing, occasionally we explore other parts of the search graph.

As the search continues deeper into the search graph, we are more likely to have found the start of the best path, and need to decrease the probability of choosing a state other than the first state. Thus, as time progresses, simulated annealing becomes more like A* search. To implement simulated annealing, the likelihood of choosing a state in the sorted agenda can be proportional to the ratio of the total cost plus evaluation function of the best state on the agenda to the total cost plus evaluation function of the given state. For example, if the first state had a total cost plus evaluation function of 20, and the second state had a cost plus evaluation function of 40, we would be half as likely to select the second state than the first state. Likelihoods can be converted to probabilities by dividing by their total.

As we progress in our search, we want the likelihood of choosing states other then the first state in the sorted agenda to decrease. We do this by dividing the likelihood for each item except the first item by the time elapsed in the search. The method used to measure the time elapsed in the search is to count the number of steps we have progressed in the search. As the search progresses, this will result in a lower and lower likelihood of choosing a state other than the first state in the sorted agenda.

F. TEST SETUP

Because the algorithms implemented in this thesis were written in different languages, a program for generating test cases for input was necessary. The program was written in Java and outputs the following information to a text file which can be read by the algorithms:

Number of jobs to be scheduled

Number of machines in the network

ETC matrix

Deadlines for each job

Precedence constraints among jobs

Three levels of precedence constraints were modeled: low level, medium level, and high level. A low level of precedence constraints is achieved by filling the entire dependency array with zeros. A high level of precedence constraints is achieved by filling the portion of the dependency array below and to the left of the arrays diagonal with ones, and filling the rest of the array with zeros. A medium level of precedence constraints is achieved by filling the portion of the dependency array below and to the left of the arrays diagonal with some ones and some zeros.

Professor Neil Rowe provided the framework of the A* algorithm written in LISP. Utility functions were written by myself to interact it.

DISCUSSION OF RESULTS

The greedy algorithm, A* search algorithm, and the simulated annealing algorithm were run to produce schedules. The greedy algorithm was written in Java, and the A* and simulated annealing algorithms were written in LISP. We varied the parameters listed for the test cases in the last section. The results of the scheduling give:

The machine on which the job should be executed

The expected start time of the job on the selected machine

The expected completion time of the job on the selected machine

The time the last job completes over all machines

The overhead of the program (how long it took the program to compute the schedule)

Table 1 shows a summary of these test runs. Two criteria can compare algorithms: the time the last job completes, and the program overhead. With relatively simple scheduling problems, we see that the schedules produced by the three algorithms provide similarly good schedules. As the difficulty of the scheduling problem increases (the number of jobs needing to be scheduled increases), the A* search algorithm and the simulated annealing algorithm produce better schedules than the greedy algorithm. This was expected, as the greedy algorithm is not making necessarily wise choices. But as the difficulty of scheduling increases, the computation time increases faster for A* and simulated annealing than for the greedy algorithm. Although Table 1 shows no increase in algorithm overhead for the greedy algorithm as the difficulty of the scheduling problem increases from 10 jobs to 50 jobs to 100 jobs, an increase was seen with much more difficult scheduling problems.

Another point of interest is comparing A* and simulated annealing. Note that for the scheduling problems with high and medium-level precedence constraints, the simulated annealing algorithm did not find a solution faster than the A* algorithm. However, with no precedence constraints the simulated annealing algorithm did find a solution faster than the A* algorithm. The original intent of modifying the A* algorithm to a simulated annealing algorithm was to produce an algorithm with behaviors similar to an A* search, but which would find solutions in complex search problems faster than A*. Whether this has been accomplished is inconclusive at this point. A wider variety of test runs or different input data may be required to resolve this question.

	Greedy Algorithm Time last job finishes	A* Algorithm Time last job finishes	Simulated Annealing Algorithm Time last job finishes	Greedy Algorithm Algorithm compute time	A* Algorithm Algorithm compute time	Simulated Annealing Algorithm Algorithm compute time
10 jobs 10 machines	16	13	13	10 ms	52 s	57 s
50 jobs 10 machines	64	40	40	10 ms	660 s	582 s
100 jobs 10 machines	387	96	96	10 ms	70224 s	66722 s

Scheduling results with no precedence constraints among jobs

	Greedy Algorithm Time last job finishes	A* Algorithm Time last job finishes	Simulated Annealing Algorithm Time last job finishes	Greedy Algorithm Algorithm compute time	A* Algorithm Algorithm compute time	Simulated Annealing Algorithm Algorithm compute time
10 jobs 10 machines	34	25	25	10 ms	10 s	12 s
50 jobs 10 machines	576	285	285	10 ms	101 s	122 s
100 jobs 10 machines	1621	596	596	10 ms	9883 s	12333 s

Scheduling results with moderate precedence constraints among jobs

	Greedy Algorithm Time last job finishes	A* Algorithm Time last job finishes	Simulated Annealing Algorithm Time last job finishes	Greedy Algorithm Algorithm compute time	A* Algorithm Algorithm compute time	Simulated Annealing Algorithm Algorithm compute time
10 jobs 10 machines	47	34	34	10 ms	1 s	1 s
50 jobs 10 machines	718	322	322	10 ms	20 s	32 s
100 jobs 10 machines	1751	788	788	10 ms	1977 s	2211 s

Scheduling results with high precedence constraints among jobs

Table 1. Results of scheduling using a greedy algorithm, A* search algorithm, and simulated annealing algorithm with various level of precedence constraints among jobs.

THIS PAGE INTENTIONALLY LEFT BLANK

cONCLUSION

The implementation of a variety of algorithms with different heuristics and different properties is useful in scheduling. Simple algorithms produce results quicker than more complicated algorithms, but the schedules they produce are usually not as good as the schedules produced by the more complicated algorithms. Because of these offsetting performance criteria, a detailed analysis using a variety of input cases must be performed to determine which algorithms should be used for which input cases. The information gained by such an analysis would be useful in the implementation of a scheduler. The scheduler could analyze the makeup of a scheduling problem, compare that to various test cases, and choose the algorithm to do the scheduling that will perform best under initial conditions of the scheduling problem.

Future work which could extend this thesis could include:

Implementing other scheduling algorithms and comparing performance

Modeling the ETC values to known or expected inputs of a specific problem

Modeling the deadline values to known or expected deadlines of a specific problem

Modeling the precedence constraints to known or expected precedence constraints of a specific problem

Implementation of a GUI-based simulation tool giving the tester a user-friendly graphical way to alter input conditions and view scheduling results

THIS PAGE INTENTIONALLY LEFT BLANK

APPENDIX A: TEXT OF THE PROGRAM

public class scheduler implements setupConstants {

public static int NUM_TASKS = 0;

public static int NUM_MACHINES = 0;

public static long START_TIME = 0;

public static long FINISH_TIME = 0;

public static long COMPUTE_TIME = 0;

public static int ETC[][];

public static int DEADLINE[];

public static int DEPENDENCIES[][];

public static int CHECKSUM[];

public static int SCHEDULE_SUMMARY[][];

public static String TASK_ORDER[][];

public static boolean TASK_STATUS[];

public static boolean MACHINE_STATUS[];

generateMatrices generate;

generateTestFiles test;

generateResultFiles result;

displayMatrices display;

search_Greedy greedy;

//********************************

//ARGUMENTED CONSTRUCTOR

//********************************

public scheduler( int numtasks, int nummachines, String filename )

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

SCHEDULE_SUMMARY = new int[NUM_TASKS][4];

generate = new generateMatrices(NUM_TASKS,NUM_MACHINES);

display = new displayMatrices(NUM_TASKS,NUM_MACHINES);

greedy = new search_Greedy(NUM_TASKS,NUM_MACHINES);

test = new generateTestFiles(NUM_TASKS,NUM_MACHINES,filename);

result = new generateResultFiles(NUM_TASKS,NUM_MACHINES,filename);

ETC = generate.generateETC();

DEADLINE = generate.generateDeadlines();

DEPENDENCIES = generate.generateDependencies(dependency_type);

CHECKSUM = generate.generateCheckSum(DEPENDENCIES);

TASK_ORDER = generate.initializeTaskOrder();

TASK_STATUS = generate.initializeTaskStatus();

MACHINE_STATUS = generate.initializeMachineStatus();

display.displayInitialization(ETC,DEADLINE,DEPENDENCIES,CHECKSUM);

test.createTestFile(ETC,DEPENDENCIES,DEADLINE);

}//END CONSTRUCTOR

//********************************

//SCHEDULE THE META-TASK

//********************************

public void scheduleMetaTask()

{

START_TIME = System.currentTimeMillis();

SCHEDULE_SUMMARY = greedy.search(ETC,TASK_STATUS,MACHINE_STATUS,TASK_ORDER,CHECKSUM,DEPENDENCIES,SCHEDULE_SUMMARY);

FINISH_TIME = System.currentTimeMillis();

result.createSummaryFile(SCHEDULE_SUMMARY,START_TIME,FINISH_TIME);

}//END METHOD "schedule"

//********************************

//DRIVER

//********************************

public static void main(String args[])

{

if (args.length < 3 || args.length > 3){

System.err.println("USAGE: java TwoDArray <1>#tasks <2>#machines <3>filename");

System.exit(1);

}

scheduler ETC = new scheduler(Integer.parseInt(args[0]),

Integer.parseInt(args[1]),

args[2]);

ETC.scheduleMetaTask();

}// END METHOD "main"

}// END CLASS "scheduler"

import java.util.Random;

public class generateMatrices implements setupConstants{

public int NUM_TASKS;

public int NUM_MACHINES;

//use seed value to allow repeatable experiments

long seedValue = 0;

Random r = new Random( seedValue );

//********************************

//ARGUMENTED CONSTRUCTOR

//********************************

public generateMatrices(int numtasks, int nummachines)

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

}//END CONSTRUCTOR

//********************************

//GENERATE THE ETC MATRIX

//********************************

public int[][] generateETC()

{

int ETC[][] = new int[NUM_TASKS][NUM_MACHINES];

for(int task = 0; task < NUM_TASKS; task++)

{

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

ETC[task][machine] = Math.abs(r.nextInt()) % ETC_RANGE + 1;

}

return ETC;

}//END METHOD "generateETC"

//********************************

//GENERATE DEADLINES

//********************************

public int[] generateDeadlines()

{

int DEADLINE[] = new int[NUM_TASKS];

for(int task = 0; task < NUM_TASKS; task++)

{

DEADLINE[task] = Math.abs(r.nextInt()) % ETC_RANGE + 1;

}

return DEADLINE;

}//END METHOD "generateDeadlines"

//********************************

//GENERATE DEPENDENCIES

//********************************

public int[][] generateDependencies( int dependency_type )

{

int DEPENDENCIES[][] = new int[NUM_TASKS][NUM_TASKS];

double random_dependency;

for(int first_task = 0; first_task < NUM_TASKS; first_task++)

{

for(int second_task = 0; second_task < NUM_TASKS; second_task++)

{

//set diagonal of dependency matrix to zeros

//--> a task can't be dependent on itself

//also set lower half of dependency matrix to zeros

//--> eliminate the possibility for cyclical dependencies

if( first_task <= second_task )

{

DEPENDENCIES[first_task][second_task] = 0;

}

//full dependencies

else if(dependency_type == FULL_DEPENDENCY)

{

DEPENDENCIES[first_task][second_task] = 1;

}

//no dependencies

else if(dependency_type == NO_DEPENDENCY)

{

DEPENDENCIES[first_task][second_task] = 0;

}

//randomly generated dependencies

else if(dependency_type == RANDOM_DEPENDENCY)

{

random_dependency = Math.random();

if(random_dependency < 0.5)

DEPENDENCIES[first_task][second_task] = 0;

else

DEPENDENCIES[first_task][second_task] = 1;

}

return DEPENDENCIES;

}//END METHOD "generateDependencies"

//**********************************

//TRANSITIVE CLOSURE OF DEPENDENCIES

//**********************************

public int[][] transitiveClosureOfDependencies( int DEPENDENCIES[][] )

{

// USE TRANSITIVE CLOSURE ALGORITHM HERE

}//END METHOD "transitiveClosureOfDependencies"

//********************************

//CHECK-SUM OF DEPENDENCY MATRIX

//********************************

public int[] generateCheckSum( int DEPENDENCIES[][] )

{

int CHECKSUM[] = new int[NUM_TASKS];

for(int first_task = 0; first_task < NUM_TASKS; first_task++)

{

for(int second_task = 0; second_task < NUM_TASKS; second_task++)

{

if( DEPENDENCIES[first_task][second_task] == 1)

CHECKSUM[second_task]++;

}

return CHECKSUM;

}//END METHOD "generateCheckSum"

//********************************

//INITIALIZE TASK ORDER

//********************************

public String[][] initializeTaskOrder()

{

String TASK_ORDER[][] = new String[NUM_TASKS][NUM_MACHINES];

for(int task = 0; task < NUM_TASKS; task++)

{

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

TASK_ORDER[task][machine] = "NO";

}

return TASK_ORDER;

}//END METHOD "initializeTaskOrder"

//********************************

//INITIALIZE TASK STATUS

//********************************

public boolean[] initializeTaskStatus()

{

boolean TASK_STATUS[] = new boolean[NUM_TASKS];

for(int task = 0; task < NUM_TASKS; task++)

{

TASK_STATUS[task] = false;

}

return TASK_STATUS;

}//END METHOD "initializeTaskStatus"

//********************************

//INITIALIZE MACHINE STATUS

//********************************

public boolean[] initializeMachineStatus()

{

boolean MACHINE_STATUS[] = new boolean[NUM_MACHINES];

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

MACHINE_STATUS[machine] = false;

}

return MACHINE_STATUS;

}//END METHOD "initializeMachineStatus"

//********************************

//INITIALIZE MACHINE ETC

//********************************

public int[] initializeMachineETC()

{

int MACHINE_ETC[] = new int[NUM_MACHINES];

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

MACHINE_ETC[machine] = 0;

}

return MACHINE_ETC;

}//END METHOD "initializeMachineETC"

}//END CLASS "generateMatrices"

//creates and writes to a file using printstream object

import java.io.*;

import java.awt.*;

public class generateTestFiles

{

public PrintStream ps;

IOS os = new IOS();

public int NUM_TASKS;

public int NUM_MACHINES;

public generateTestFiles(int numtasks, int nummachines, String filename)

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

String file = new String(filename);

try {

ps = new PrintStream(

new FileOutputStream(filename));

}

catch( IOException e ) {

System.err.println("File not opened properly\n" +

e.toString());

System.exit(1);

}

public void addTestSetup()

{

ps.println(NUM_TASKS);

ps.println(NUM_MACHINES);

ps.println();

}

public void addETC( int ETC[][] )

{

for(int i = 0; i < NUM_TASKS; i++)

{

for(int j = 0; j < NUM_MACHINES; j++)

{

os.setJustify(IOS.LEFT);

os.setWidth(5);

os.print(ps,ETC[i][j]);

}

ps.println();

}

ps.println();

}

public void addDependencies( int DEPENDENCIES[][] )

{

for(int i = 0; i < NUM_TASKS; i++)

{

for(int j = 0; j < NUM_TASKS; j++)

{

os.setJustify(IOS.LEFT);

os.setWidth(5);

os.print(ps,DEPENDENCIES[i][j]);

}

ps.println();

}

ps.println();

}

public void addDeadline( int DEADLINE[] )

{

for(int i = 0; i < NUM_TASKS; i++)

{

os.setJustify(IOS.LEFT);

os.setWidth(5);

os.print(ps,DEADLINE[i]);

ps.println();

}

public void createTestFile( int ETC[][],

int DEPENDENCIES[][],

int DEADLINE[] )

{

System.out.println("Generating Test File....");

System.out.println();

addTestSetup();

addETC(ETC);

addDependencies(DEPENDENCIES);

addDeadline(DEADLINE);

}

public class search_Greedy implements setupConstants {

// *** Performance Metric ***

// Simply review the estimated time to complete (ETC) matrix

// and choose the task on the machine which will run fastest

// *** Algorithm Description ***

// 1. Find the minimum ETC for each task --

// take into consideration also time which each machine is available

// 2. Choose the minimum of the minimums (i.e., the min-min

// algorithm), and schedule that task

// 3. Update the task status and machine status to indicate

// which tasks are scheduled, and which machines are running

// 4. Do steps 1 thru 3 until all tasks are scheduled

public int NUM_TASKS;

public int NUM_MACHINES;

int[] MACHINE_STOP_TIME;

displayMatrices display;

//********************************

//ARGUMENTED CONSTRUCTOR

//********************************

public search_Greedy(int numtasks, int nummachines)

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

MACHINE_STOP_TIME = new int[NUM_MACHINES];

display = new displayMatrices(NUM_TASKS,NUM_MACHINES);

for(int i = 0; i < NUM_MACHINES; i++)

{

MACHINE_STOP_TIME[i] = 0;

}

}//END CONSTRUCTOR

//********************************

//PERFORM GREEDY SEARCH

//********************************

public int[][] search(int[][] ETC, boolean[] TASK_STATUS, boolean[] MACHINE_STATUS,

String[][] TASK_ORDER, int[] CHECKSUM, int[][] DEPENDENCIES,

int[][] SCHEDULE_SUMMARY)

{

int minETC;

int MIN_ETC = 10000;

int scheduledTask = 0;

int scheduledMachine = 0;

int tasks_completed = 0;

System.out.println("Commence scheduling.....");

System.out.println();

//ENSURE ALL TASKS ARE SCHEDULED

for(int schedule = 0; schedule < NUM_TASKS; schedule++)

{

minETC = MIN_ETC;

//FIND THE MINIMUM IN THE ETC ARRAY

for(int task = 0; task < NUM_TASKS; task++)

{

//ENSURE TASK HAS NOT BEEN SCHEDULED

//ENSURE TASK HAS NO IMMEDIATE DEPENDENCY

if(TASK_STATUS[task] == false &&

CHECKSUM[task] == 0)

{

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

if( (ETC[task][machine] + MACHINE_STOP_TIME[machine]) < minETC)

{

minETC = ETC[task][machine];

scheduledTask = task;

scheduledMachine = machine;

}

//update number of tasks completed

tasks_completed++;

//inform user of scheduling status

System.out.println("Scheduling TASK #" + Integer.toString(scheduledTask) +

" on MACHINE #" + Integer.toString(scheduledMachine) +

" at time " + Integer.toString(MACHINE_STOP_TIME[scheduledMachine]));

SCHEDULE_SUMMARY[schedule][0] = scheduledTask;

SCHEDULE_SUMMARY[schedule][1] = scheduledMachine;

SCHEDULE_SUMMARY[schedule][2] = MACHINE_STOP_TIME[scheduledMachine];

SCHEDULE_SUMMARY[schedule][3] = MACHINE_STOP_TIME[scheduledMachine] +

ETC[scheduledTask][scheduledMachine];

MACHINE_STOP_TIME[scheduledMachine] = MACHINE_STOP_TIME[scheduledMachine] +

ETC[scheduledTask][scheduledMachine];

//update matrices

TASK_ORDER[scheduledTask][scheduledMachine] = Integer.toString(schedule);

TASK_STATUS[scheduledTask] = true;

MACHINE_STATUS[scheduledMachine] = true;

if(tasks_completed < NUM_TASKS)

{

CHECKSUM = reviseCHECKSUM(CHECKSUM,DEPENDENCIES,scheduledTask);

}

else

{

System.out.println("\nScheduling complete.....\n");

}

return SCHEDULE_SUMMARY;

}//END METHOD "search"

//********************************

//REVISE THE CHECKSUM MATRIX

//********************************

public int[] reviseCHECKSUM(int[] CHECKSUM, int[][] DEPENDENCIES, int scheduledTask)

{

if( DISPLAY_MATRIX == true )

{

System.out.println("************************");

System.out.println("*** REVISE CHECKSUM()***");

System.out.println("************************");

System.out.println();

}

for(int second_task = 0; second_task < NUM_TASKS; second_task++)

{

if( DEPENDENCIES[scheduledTask][second_task] == 1)

CHECKSUM[second_task]--;

}

if( DISPLAY_MATRIX == true )

display.display1D_Integer_Matrix(CHECKSUM);

return CHECKSUM;

}//END METHOD "reviseCHECKSUM"

}// END CLASS "search_Greedy"

//creates and writes to a file using printstream object

import java.io.*;

import java.awt.*;

public class generateResultFiles

{

public PrintStream ps;

IOS os = new IOS();

public int NUM_TASKS;

public int NUM_MACHINES;

public generateResultFiles(int numtasks,int nummachines,String filename)

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

String file = new String("greedysummary_" + filename);

try {

ps = new PrintStream(new FileOutputStream(file));

}

catch( IOException e ) {

System.err.println("File not opened properly\n" +

e.toString());

System.exit(1);

}

public void addSummaryHeaders()

{

os.setJustify(IOS.LEFT);

os.setWidth(14);

os.print(ps,"JOB#");

os.setJustify(IOS.LEFT);

os.setWidth(14);

os.print(ps,"MACHINE#");

os.setJustify(IOS.LEFT);

os.setWidth(14);

os.print(ps,"START TIME");

os.setJustify(IOS.LEFT);

os.setWidth(14);

os.print(ps,"FINISH TIME");

ps.println();

}

public void addScheduleSummary( int schedule_summary[][],

long start,

long finish )

{

for(int task = 0; task < NUM_TASKS; task++)

{

for(int displaycolumns = 0; displaycolumns < 4; displaycolumns++)

{

os.setJustify(IOS.LEFT);

os.setWidth(14);

os.print(ps,schedule_summary[task][displaycolumns]);

}

ps.println();

}

ps.println();

ps.println("Algorithm Compute Time: " +

Long.toString(finish - start) +

" milliseconds");

ps.println("Meta-task Completion Time: " +

Integer.toString(getMetaTaskFinishTime(schedule_summary)));

}

public int getMetaTaskFinishTime( int[][] schedule_summary )

{

int meta_task_finish_time = 0;

for(int i = 0; i < NUM_TASKS; i++)

{

if(schedule_summary[i][3] > meta_task_finish_time)

meta_task_finish_time = schedule_summary[i][3];

}

return meta_task_finish_time;

}//END METHOD "getMetaTaskFinishTime"

public void createSummaryFile( int schedule_summary[][],

long start,

long finish )

{

System.out.println("Generating Result File....");

System.out.println();

addSummaryHeaders();

addScheduleSummary(schedule_summary,start,finish);

}

public class displayMatrices implements setupConstants {

public int NUM_TASKS;

public int NUM_MACHINES;

//class IOS allows text formatting similar to C++

IOS os = new IOS();

//********************************

//ARGUMENTED CONSTRUCTOR

//********************************

public displayMatrices(int numtasks, int nummachines)

{

NUM_TASKS = numtasks;

NUM_MACHINES = nummachines;

}//END CONSTRUCTOR

//********************************

//DISPLAY 1D INTEGER ARRAY - TASKS

//********************************

public void display1D_Integer_Matrix( int matrix[] )

{

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

os.setWidth(13);

os.println(System.out,matrix[task]);

}// END FOR

System.out.println();

}//END METHOD "displayMatrix"

//********************************

//DISPLAY 1D INTEGER ARRAY - MACHINES

//********************************

public void display1D_Integer_Machine_Matrix( int matrix[] )

{

displayMachineHeaders();

System.out.print("ETC ");

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,matrix[machine]);

}// END FOR

System.out.println();

}//END METHOD "display1D_Integer_Machine_Matrix"

//********************************

//DISPLAY 1D BOOLEAN ARRAY

//********************************

public void display1D_BOOL_Matrix( boolean matrix[] )

{

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

System.out.println(matrix[task]);

}// END FOR

System.out.println();

}//END METHOD "display1D_BOOL_Matrix"

//********************************

//DISPLAY 1D STRING ARRAY

//********************************

public void display1D_String_Matrix( String matrix[] )

{

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

System.out.println(matrix[task]);

}// END FOR

System.out.println();

}//END METHOD "display1D_String_Matrix"

//********************************

//DISPLAY 1D FLOAT ARRAY

//********************************

public void display1D_Float_Matrix( double matrix[] )

{

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

System.out.println(matrix[task]);

}// END FOR

System.out.println();

}//END METHOD "display1D_String_Matrix"

//********************************

//DISPLAY 2D INTEGER ARRAY

//********************************

public void display2D_Integer_Matrix( int matrix[][] )

{

displayMachineHeaders();

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,matrix[task][machine]);

}// END FOR

System.out.println();

}// END FOR

System.out.println();

}//END METHOD "display2D_Integer_Matrix"

//********************************

//DISPLAY SCHEDULING ARRAY

//********************************

public void displaySchedulingSummary( int schedule_summary[][] )

{

// displayMachineHeaders();

for(int task = 0; task < NUM_TASKS; task++)

{

for(int displaycolumns = 0; displaycolumns < 4; displaycolumns++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,schedule_summary[task][displaycolumns]);

}// END FOR

System.out.println();

}// END FOR

System.out.println();

}//END METHOD "displaySchedulingSummary"

//********************************

//DISPLAY 2D DEPENDENCY ARRAY

//********************************

public void display2D_Dependency_Matrix( int matrix[][] )

{

displayTaskHeaders();

for(int task1 = 0; task1 < NUM_TASKS; task1++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task1);

for(int task2 = 0; task2 < NUM_TASKS; task2++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,matrix[task1][task2]);

}// END FOR

System.out.println();

}// END FOR

System.out.println();

}//END METHOD "display2D_Dependency_Matrix"

//********************************

//DISPLAY 2D STRING ARRAY

//********************************

public void display2D_String_Matrix( String matrix[][] )

{

displayMachineHeaders();

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,matrix[task][machine]);

}// END FOR

System.out.println();

}// END FOR

System.out.println();

}//END METHOD "display2D_Integer_Matrix"

//********************************

//DISPLAY 2D DOUBLE ARRAY

//********************************

public void display2D_Double_Matrix( double matrix[][] )

{

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(6);

os.print(System.out,"TASK#");

os.setWidth(4);

os.print(System.out,task);

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

os.setJustify(IOS.LEFT);

os.setWidth(13);

os.print(System.out,matrix[task][machine]);

}// END FOR

System.out.println();

}// END FOR

System.out.println();

}//END METHOD "displayMatrix"

//********************************

//DISPLAY MACHINE HEADERS

//********************************

public void displayMachineHeaders()

{

System.out.print(" ");

for(int machine = 0; machine < NUM_MACHINES; machine++)

{

os.setJustify(IOS.LEFT);

os.setWidth(9);

os.print(System.out,"MACHINE #");

os.setWidth(4);

os.print(System.out,machine);

}// END FOR

System.out.println();

}// END METHOD "displayColumnHeaders"

//********************************

//DISPLAY TASK HEADERS

//********************************

public void displayTaskHeaders()

{

System.out.print(" ");

for(int task = 0; task < NUM_TASKS; task++)

{

os.setJustify(IOS.LEFT);

os.setWidth(9);

os.print(System.out,"TASK# ");

os.setWidth(4);

os.print(System.out,task);

}// END FOR

System.out.println();

}// END METHOD "displayTaskHeaders"

//********************************

//DISPLAY INITIAL SET UP

//********************************

public void displayInitialization(int[][] ETC, int[] DEADLINE, int[][] DEPENDENCIES,

int[] CHECKSUM)

{

if( DISPLAY_MATRIX == true )

{

System.out.println("************************");

System.out.println("*** INITIALIZING ETC ***");

System.out.println("************************");

System.out.println();

display2D_Integer_Matrix( ETC );

System.out.println("************************");

System.out.println("*** DEADLINES ***");

System.out.println("************************");

System.out.println();

display1D_Integer_Matrix( DEADLINE );

System.out.println("************************");

System.out.println("*** DEPENDENCIES ***");

System.out.println("************************");

System.out.println();

display2D_Dependency_Matrix( DEPENDENCIES );

System.out.println("************************");

System.out.println("*** CHECK SUM ***");

System.out.println("************************");

System.out.println();

display1D_Integer_Matrix( CHECKSUM );

}

}//END METHOD "displayInitialization"

}//END CLASS "displayMatrices"

* Frederick F. Chew, The Java/C++ Cross Reference Handbook (Book/CD-ROM)

* Published By HP Press/Prentice-Hall

* Permission to use, copy, modify, and distribute this

* software and its documentation for NON-COMMERCIAL purposes

* and without fee is hereby granted provided that this

* copyright notice appears in all copies.

* THE AUTHOR AND PUBLISHER MAKE NO REPRESENTATIONS OR

* WARRANTIES ABOUT THE SUITABILITY OF THE SOFTWARE, EITHER

* EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE

* IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A

* PARTICULAR PURPOSE, OR NON-INFRINGEMENT. THE AUTHOR

* AND PUBLISHER SHALL NOT BE LIABLE FOR ANY DAMAGES SUFFERED

* BY LICENSEE AS A RESULT OF USING, MODIFYING OR DISTRIBUTING

* THIS SOFTWARE OR ITS DERIVATIVES.

/**

* @version 1.00 01 May 1997

* @author Frederick F. Chew

/**

* Note: This program was built from the JDK version 1.02

* and has not been customized to work on version 1.1

* The precision of floating point numbers has undergone

* change in version 1.1

import java.awt.*;

import java.io.*;

public class IOS {

public IOS() {

radix = DEC;

width = 0;

fillchar = ' ';

justify_right = RIGHT;

precision = 6;

upper_case = false;

show_sign = false;

internal_pad = false;

fixed_format = FIXED;

}

public IOS(int base, int size, char fill, boolean just, int significant, boolean cap,

boolean sign, boolean pad, boolean format) {

if ((base < 0) || (base > 2))

base = DEC;

if (size < 0)

size = 0;

radix = base;

width = size;

fillchar = fill;

justify_right = just;

precision = significant;

upper_case = cap;

show_sign = sign;

internal_pad = pad;

fixed_format = format;

}

// public mutator methods for IOS attributes

public int setRadix(int base) {

int org_radix = radix;

if ((base < 0) || (base > 2))

base = DEC;

radix = base;

return org_radix;

}

public int setWidth(int size) {

int org_width = width;

if (size < 0)

size = 0;

width = size;

return org_width;

}

public char setFill(char fill) {

char org_fillchar = fillchar;

fillchar = fill;

return org_fillchar;

}

public boolean setJustify(boolean just) {

boolean org_just = justify_right;

justify_right = just;

return org_just;

}

public int setPrecision(int prec) {

int org_precision = precision;

precision = prec;

return org_precision;

}

public boolean setUpperCase(boolean cap) {

boolean org_upper_case = upper_case;

upper_case = cap;

return org_upper_case;

}

public boolean setShowSign(boolean sign) {

boolean org_show_sign = show_sign;

show_sign = sign;

return org_show_sign;

}

public boolean setInternalPad(boolean pad) {

boolean org_internal_pad = pad;

internal_pad = pad;

return org_internal_pad;

}

public boolean setNumericalFormat(boolean format) {

boolean org_fixed_format = fixed_format;

fixed_format = format;

return org_fixed_format;

}

void showState(PrintStream ps) {

String radix_str = "";

String width_str = "";

String just_str = "";

String fillchar_str = "";

String format_str = "";

switch (radix) {

case DEC: radix_str += "Decimal";

break;

case OCT: radix_str += "Octal";

break;

case HEX: radix_str += "Hexadecimal";

break;

}

if (width == 0)

width_str += "Default";

else

width_str += width;

if (justify_right)

just_str += "RIGHT";

else

just_str += "LEFT";

if (fillchar == ' ')

fillchar_str += "Space";

else

fillchar_str += fillchar;

if (fixed_format)

format_str += "Fixed";

else

format_str += "Scientific";

ps.println();

ps.println("Radix = "+radix_str);

ps.println("Width = "+width_str);

ps.println("Fill Character = "+fillchar_str);

ps.println("Justification = "+just_str);

ps.println("Precision = "+precision);

ps.println("Upper case = "+upper_case);

ps.println("Show sign = "+show_sign);

ps.println("Internal pad = "+internal_pad);

ps.println("Numerical format = "+format_str);

ps.println();

}

// public methods for print() and println()

public void println(PrintStream ps, char aChar) {

String newStr = "";

newStr += aChar;

print(ps, newStr);

ps.println();

}

public void println(PrintStream ps, char [] aCharArray) {

String newStr = "";

newStr += aCharArray;

print(ps, newStr);

ps.println();

}

public void println(PrintStream ps, int anInt) {

println(ps, (long)anInt);

}

public void println(PrintStream ps, long aLong) {

print(ps, aLong);

ps.println();

}

public void println(PrintStream ps, float aFlt) {

println(ps, (double) aFlt);

}

public void println(PrintStream ps, double aDbl) {

print(ps, aDbl);

ps.println();

}

public void println(PrintStream ps, String aStr) {

print(ps, aStr);

ps.println();

}

public void print(PrintStream ps, char aChar) {

String newStr = "";

newStr += aChar;

print(ps, newStr);

}

public void print(PrintStream ps, char [] aCharArray) {

String newStr = "";

newStr += aCharArray;

print(ps, newStr);

}

public void print(PrintStream ps, int anInt) {

print(ps, (long)anInt);

}

public void print(PrintStream ps, long aLong) {

String newStr = "";

if ((show_sign) && (aLong > 0))

newStr += "+";

switch (radix) {

case DEC: newStr += aLong;

break;

case OCT: newStr += "0" + newBase(aLong, 3, 7, "01234567");

break;

case HEX: if (upper_case)

newStr += "0X" + newBase(aLong, 4, 15, "0123456789ABCDEF");

else

newStr += "0x" + newBase(aLong, 4, 15, "0123456789abcdef");

break;

}

print(ps, newStr);

}

public void print(PrintStream ps, float aFlt) {

print(ps, (double)aFlt);

}

public void print(PrintStream ps, double aDbl) {

String newStr = "";

String tmpStr = "";

if (fixed_format)

tmpStr += prepareFixedFormat(aDbl);

else

tmpStr += prepareScientificFormat(aDbl);

newStr += padString(tmpStr, aDbl);

print(ps, newStr);

}

public void print(PrintStream ps, String aStr) {

ps.print(prepareField(aStr));

ps.flush();

}

// private helper methods

private void drawRuler(PrintStream ps) {

String interval = new String("1234567890");

String ruler = "";

for (int index = 0; index < 6; index++)

ruler += interval;

ps.println();

ps.println(ruler);

ps.println();

}

private String newBase(long value, int no_of_bits, int one_bits, String digits) {

String result = "";

if (value == 0) {

result += "0";

}

else {

while (value != 0) {

result = digits.charAt((int)(value & one_bits)) + result;

value = value >>> no_of_bits;

}

return result;

}

private String prepareField(String aStr) {

if (width == 0) {

return aStr;

}

if (width <= aStr.length()) {

return aStr;

}

String newStr = "";

int delta = width - aStr.length();

if (justify_right) { // RIGHT

for (int index = 0; index < delta; index++)

newStr += fillchar;

newStr += aStr;

}

else { // LEFT

StringBuffer sbuffer = new StringBuffer(aStr);

char [] cbuffer = new char[delta];

sbuffer.append(cbuffer);

for (int index = 0; index < delta; index++)

sbuffer.setCharAt(aStr.length()+index, fillchar);

newStr += new String(sbuffer);

}

return newStr;

}

private String eNotation(char sign, long exponent) {

String expStr = new Long(exponent).toString();

int leading_zeros = 3 - (expStr.length());

String result = "";

result += (upper_case)?"E":"e";

result += sign;

for (int index = 0; index < leading_zeros; index++)

result += "0";

result += expStr;

return result;

}

private String moveDecimalLeft(long aLong) {

String result = "";

String str = "";

str += aLong;

result += str.substring(0, 1) + "." + str.substring(1, str.length());

return result;

}

private String moveDecimalRight(String str) {

char ch;

long pwr = 0;

int index2 = 0;

String result = "";

String newStr = "";

for (int index1 = 0; index1 < str.length(); index1++) {

if ((ch = str.charAt(index1)) == '0')

pwr++;

else

newStr += ch;

}

pwr++;

if ((newStr.substring(1, newStr.length())).length() != 0)

result += newStr.substring(0, 1) + "." + newStr.substring(1, newStr.length()) + eNotation('-', pwr);

else

result += newStr.substring(0, 1) + "." + "0" + eNotation('-', pwr);

return result;

}

private boolean alreadyScientific(String str) {

boolean flag = false;

for(int index=0; index < str.length(); index++) {

if ( (str.charAt(index) == 'e') || (str.charAt(index) == 'E') )

flag = true;

}

return flag;

}

private String improveDefault(String str) {

boolean decimal_pt = false;

int e_index = 0;

for (int index = 0; index < str.length(); index++) {

if (str.charAt(index) == '.')

decimal_pt = true;

else

if ( (str.charAt(index) == 'e') || (str.charAt(index) == 'E') )

e_index = index;

}

String result = "";

if (decimal_pt) {

result += str.substring(0, e_index) + (upper_case?"E":"e") + str.substring(e_index+1, str.length());

}

else {

result += str.substring(0, e_index) + ".0" + (upper_case?"E":"e") + str.substring(e_index+1, str.length());

}

return result;

}

private String padString(String str, double num) {

int lgth = width - str.length();

if (((show_sign) || (num < 0.0)) && (lgth > 0) && (internal_pad)) {

String result = "";

result += str.substring(0, 1);

for (int index = 0; index < lgth; index++) result += fillchar;

result += str.substring(1, str.length());

return result;

}

return str;

}

private String prepareScientificFormat(double aDbl) {

String result = "";

// The double may already be in scientific format

String dblStr = "";

dblStr += aDbl;

if (alreadyScientific(dblStr)) {

String newStr = "";

if ((show_sign) && (aDbl > 0))

newStr += "+";

newStr += improveDefault(dblStr);

return newStr;

}

// Include the sign if necessary

if (aDbl < 0.0) {

result += "-";

aDbl = -1 * aDbl;

}

else if (show_sign)

result += "+";

// Find the whole part and the fractional part

long whole = (long) aDbl;

double fraction = aDbl - whole;

String wholeStr = "";

wholeStr += whole;

if (wholeStr.length() >= precision) {

if (fraction >= 0.5) whole++;

long pwr = wholeStr.length() - 1;

result += moveDecimalLeft(whole) + eNotation('+', pwr);

}

else {

int frac_prec = precision - wholeStr.length();

if (fraction == 0.0) {

long pwr = wholeStr.length() - 1;

result += moveDecimalLeft(whole) + ((whole==0)?"0":"") + eNotation('+', pwr);

}

else

result += determineFraction(frac_prec, fraction, whole);

}

return result;

}

private String determineFraction(int prec, double aDbl, long org_whole) {

String result = "";

String aDblStr = "";

aDblStr += aDbl;

int lgth = aDblStr.length()-2;

String frac_str = "";

if (prec < lgth) {

double newDbl = aDbl;

for (int index = 0; index < prec; index++)

newDbl *= 10.0;

long sub_whole = (long)newDbl;

double sub_fraction = newDbl - sub_whole;

if (sub_fraction >= 0.5) sub_whole++;

frac_str += sub_whole;

}

else

frac_str += aDblStr.substring(2, aDblStr.length());

String orgWholeStr = "";

orgWholeStr += org_whole;

if (org_whole > 0) {

long pwr = orgWholeStr.length() - 1;

result += moveDecimalLeft(org_whole) + frac_str + eNotation('+', pwr);

}

else {

result += moveDecimalRight(frac_str);

}

return result;

}

private String prepareFixedFormat(double aDbl) {

String result = "";

// The double may already be in scientific format

String dblStr = "";

dblStr += aDbl;

if (alreadyScientific(dblStr)) {

String newStr = "";

if ((show_sign) && (aDbl > 0))

newStr += "+";

newStr += improveDefault(dblStr);

return newStr;

}

// Include the sign if necessary

if (aDbl < 0.0) {

result += "-";

aDbl = -1 * aDbl;

}

else if (show_sign)

result += "+";

// Find the whole part and the fractional part

long whole = (long) aDbl;

double fraction = aDbl - whole;

String wholeStr = "";

wholeStr += whole;

if (wholeStr.length() >= precision) {

if (fraction >= 0.5) whole++;

result += whole;

}

else {

int frac_prec = precision - wholeStr.length();

if (fraction == 0.0)

result += whole;

else

result += whole + "." + findFraction(frac_prec, fraction);

}

return result;

}

private String findFraction(int prec, double aDbl) {

String result = "";

String aDblStr = "";

aDblStr += aDbl;

int lgth = aDblStr.length()-2;

if (prec < lgth) {

double newDbl = aDbl;

for (int index = 0; index < prec; index++)

newDbl *= 10.0;

long sub_whole = (long)newDbl;

double sub_fraction = newDbl - sub_whole;

if (sub_fraction >= 0.5) sub_whole++;

result += sub_whole;

}

else

result += aDblStr.substring(2, aDblStr.length());

return result;

}

// public final fields

public static final int DEC = 0;

public static final int OCT = 1;

public static final int HEX = 2;

public static final boolean RIGHT = true;

public static final boolean LEFT = false;

public static final boolean FIXED = true;

public static final boolean SCIENTIFIC = false;

// private variable fields

private int precision;

private int radix;

private int width;

private char fillchar;

private boolean justify_right;

private boolean upper_case;

private boolean show_sign;

private boolean internal_pad;

private boolean fixed_format;

public static void main(String args[]) throws IOException {

double [] dbl1 = {

0.0, 0.1, 0.01, 0.001, 0.0001, 0.00001,

0.000001, 0.0000001, 0.00000001, 0.000000001, 0.0000000001, 0.00000000001

};

double [] dbl2 = {

0.1, 0.12, 0.123, 0.1234, 0.12345, 0.123456, 0.1234567, 0.12345678, 0.123456789,

0.1234567891, 0.12345678912, 0.123456789123, 0.1234567891234, 0.12345678912345

};

double [] dbl3 = {

0.123456, 1.123456, 12.123456, 123.123456, 1234.123456, 12345.123456, 123456.123456,

12345.6123456, 1234.56123456, 123.456123456, 12.3456123456, 1.23456123456,

1234561.23456, 12345612.3456, 123456123.456, 1234561234.56, 12345612345.6, 1234567.123456, 12345678.123456, 123456789.123456, 1234567891.123456, 12345678912.123456, 123456789123.123456, 1234567891234.123456

};

double [] dbl4 = {

1.1, 12.12, 123.123, 1234.1234, 12345.12345, 123456.123456, 1234567.1234567, 12345678.12345678, 123456789.123456789, 1234567891.1234567891, 12345678912.12345678912, 123456789123.123456789123,

1234567891234.1234567891234, 12345678912345.12345678912345, 123456789123456.123456789123456, 1234567891234567.1234567891234567, 12345678912345678.12345678912345678, 123456789123456789.123456789123456789

};

// Test01

PrintStream prs1 = new PrintStream(new FileOutputStream("OS1A.TXT"));

IOS os1A = new IOS();

String bird = "penguin";

String fish = "rock cod";

String tree = "maple";

os1A.setFill('~');

os1A.setWidth(12);

os1A.println(prs1, bird);

os1A.println(prs1, fish);

os1A.setWidth(0);

os1A.println(prs1, tree);

prs1.close();

// Test02

PrintStream prs2 = new PrintStream(new FileOutputStream("OS2A.TXT"));

IOS os2A = new IOS();

double num1 = 17.7875678;

os2A.setPrecision(8);

os2A.println(prs2, num1);

prs2.close();

// Test03

PrintStream prs3 = new PrintStream(new FileOutputStream("OS3A.TXT"));

IOS os3A = new IOS();

int num2 = 160;

os3A.setRadix(IOS.OCT);

os3A.print(prs3, "Octal = ");

os3A.println(prs3, num2);

os3A.setRadix(IOS.HEX);

os3A.print(prs3, "Hexadecimal = ");

os3A.println(prs3, num2);

os3A.setUpperCase(true);

os3A.print(prs3, "Hexadecimal = ");

os3A.println(prs3, num2);

os3A.setRadix(IOS.DEC);

os3A.print(prs3, "Decimal = ");

os3A.println(prs3, num2);

prs3.close();

// Test04

PrintStream prs4 = new PrintStream(new FileOutputStream("OS4A.TXT"));

IOS os4A = new IOS();

String feline = "bob cat";

long lnum = 757905;

double dnum = 2345070.00915756;

os4A.setJustify(IOS.LEFT);

os4A.setFill('#');

os4A.setWidth(12);

os4A.setPrecision(14);

os4A.println(prs4, feline);

os4A.println(prs4, lnum);

os4A.println(prs4, dnum);

os4A.setJustify(IOS.RIGHT);

os4A.setFill('*');

os4A.setWidth(12);

os4A.setPrecision(14);

os4A.println(prs4, feline);

os4A.println(prs4, lnum);

os4A.println(prs4, dnum);

prs4.close();

// Test05

PrintStream prs5 = new PrintStream(new FileOutputStream("OS5A.TXT"));

IOS os5A = new IOS();

os5A.setJustify(IOS.LEFT);

os5A.setFill('*');

os5A.setWidth(12);

os5A.println(prs5, bird);

os5A.println(prs5, fish);

os5A.setJustify(IOS.RIGHT);

os5A.println(prs5, tree);

prs5.close();

// Test06

PrintStream prs6 = new PrintStream(new FileOutputStream("OS6A.TXT"));

IOS os6A = new IOS();

int int1 = 34950;

int int2 = -int1;

float flt1 = 17.5829f;

float flt2 = -flt1;

os6A.setInternalPad(true);

os6A.setFill('^');

os6A.setWidth(16);

os6A.println(prs6, int1);

os6A.println(prs6, int2);

os6A.println(prs6, flt1);

os6A.println(prs6, flt2);

os6A.setInternalPad(false);

os6A.println(prs6, flt2);

prs6.close();

// Test07

PrintStream prs7 = new PrintStream(new FileOutputStream("OS7A.TXT"));

IOS os7A = new IOS();

long long1 = 875090406;

double doub1 = 395.0;

double doub2 = 7693.8356;

double doub3 = 3409.958;

os7A.println(prs7, doub1);

os7A.setShowSign(true);

os7A.println(prs7, doub1);

os7A.setNumericalFormat(IOS.SCIENTIFIC);

os7A.println(prs7, long1);

os7A.println(prs7, doub2);

os7A.println(prs7, doub3);

os7A.setShowSign(false);

os7A.setNumericalFormat(IOS.FIXED);

os7A.println(prs7, long1);

os7A.println(prs7, doub1);

os7A.println(prs7, doub2);

os7A.println(prs7, doub3);

prs7.close();

// Test08

PrintStream prs8 = new PrintStream(new FileOutputStream("OS8A.TXT"));

IOS os8A = new IOS();

os8A.setPrecision(20);

os8A.setWidth(30);

os8A.setJustify(IOS.RIGHT);

os8A.drawRuler(prs8);

os8A.println(prs8, "Default System.out.println() - Positive");

for(int index = 0; index < dbl1.length; index++)

prs8.println(dbl1[index]);

os8A.println(prs8, "Default System.out.println() - Negative");

for(int index = 0; index < dbl1.length; index++)

prs8.println(-dbl1[index]);

os8A.println(prs8, "Fixed Format - Positive");

for(int index = 0; index < dbl1.length; index++)

os8A.println(prs8, dbl1[index]);

os8A.println(prs8, "Fixed Format - Negative");

for(int index = 0; index < dbl1.length; index++)

os8A.println(prs8, -dbl1[index]);

os8A.setNumericalFormat(IOS.SCIENTIFIC);

os8A.println(prs8, "Scientific Format - Positive");

for(int index = 0; index < dbl1.length; index++)

os8A.println(prs8, dbl1[index]);

os8A.println(prs8, "Scientific Format - Negative");

for(int index = 0; index < dbl1.length; index++)

os8A.println(prs8, -dbl1[index]);

prs8.close();

// Test09

PrintStream prs9 = new PrintStream(new FileOutputStream("OS9A.TXT"));

IOS os9A = new IOS();

os9A.setPrecision(20);

os9A.setWidth(30);

os9A.setJustify(IOS.RIGHT);

os9A.drawRuler(prs9);

os9A.println(prs9, "Default System.out.println() - Positive");

for(int index = 0; index < dbl2.length; index++)

prs9.println(dbl2[index]);

os9A.println(prs9, "Default System.out.println() - Negative");

for(int index = 0; index < dbl2.length; index++)

prs9.println(-dbl2[index]);

os9A.println(prs9, "Fixed Format - Positive");

for(int index = 0; index < dbl2.length; index++)

os9A.println(prs9, dbl2[index]);

os9A.println(prs9, "Fixed Format - Negative");

for(int index = 0; index < dbl2.length; index++)

os9A.println(prs9, -dbl2[index]);

os9A.setNumericalFormat(IOS.SCIENTIFIC);

os9A.println(prs9, "Scientific Format - Positive");

for(int index = 0; index < dbl2.length; index++)

os9A.println(prs9, dbl2[index]);

os9A.println(prs9, "Scientific Format - Negative");

for(int index = 0; index < dbl2.length; index++)

os9A.println(prs9, -dbl2[index]);

prs9.close();

// Test10

PrintStream prs10 = new PrintStream(new FileOutputStream("OS10A.TXT"));

IOS os10A = new IOS();

os10A.setPrecision(20);

os10A.setWidth(30);

os10A.setJustify(IOS.RIGHT);

os10A.drawRuler(prs10);

os10A.println(prs10, "Default System.out.println() - Positive");

for(int index = 0; index < dbl3.length; index++)

prs10.println(dbl3[index]);

os10A.println(prs10, "Default System.out.println() - Negative");

for(int index = 0; index < dbl3.length; index++)

prs10.println(-dbl3[index]);

os10A.println(prs10, "Fixed Format - Positive");

for(int index = 0; index < dbl3.length; index++)

os10A.println(prs10, dbl3[index]);

os10A.println(prs10, "Fixed Format - Negative");

for(int index = 0; index < dbl3.length; index++)

os10A.println(prs10, -dbl3[index]);

os10A.setNumericalFormat(IOS.SCIENTIFIC);

os10A.println(prs10, "Scientific Format - Positive");

for(int index = 0; index < dbl3.length; index++)

os10A.println(prs10, dbl3[index]);

os10A.println(prs10, "Scientific Format - Negative");

for(int index = 0; index < dbl3.length; index++)

os10A.println(prs10, -dbl3[index]);

prs10.close();

// Test11

PrintStream prs11 = new PrintStream(new FileOutputStream("OS11A.TXT"));

IOS os11A = new IOS();

os11A.setPrecision(20);

os11A.setWidth(30);

os11A.setJustify(IOS.RIGHT);

os11A.drawRuler(prs11);

os11A.println(prs11, "Default System.out.println() - Positive");

for(int index = 0; index < dbl4.length; index++)

prs11.println(dbl4[index]);

os11A.println(prs11, "Default System.out.println() - Negative");

for(int index = 0; index < dbl4.length; index++)

prs11.println(-dbl4[index]);

os11A.println(prs11, "Fixed Format - Positive");

for(int index = 0; index < dbl4.length; index++)

os11A.println(prs11, dbl4[index]);

os11A.println(prs11, "Fixed Format - Negative");

for(int index = 0; index < dbl4.length; index++)

os11A.println(prs11, -dbl4[index]);

os11A.setNumericalFormat(IOS.SCIENTIFIC);

os11A.println(prs11, "Scientific Format - Positive");

for(int index = 0; index < dbl4.length; index++)

os11A.println(prs11, dbl4[index]);

os11A.println(prs11, "Scientific Format - Negative");

for(int index = 0; index < dbl4.length; index++)

os11A.println(prs11, -dbl4[index]);

prs11.close();

System.out.println("(press Enter to exit)");

try {

System.in.read();

}

catch (IOException e) {

return;

}

public interface setupConstants {

public final static int ETC_RANGE = 40;

public final static boolean DISPLAY_MATRIX = false;

public final static boolean DISPLAY_TASKS = false;

public final static int FULL_DEPENDENCY = 0;

public final static int NO_DEPENDENCY = 1;

public final static int RANDOM_DEPENDENCY = 2;

public final static int GREEDY = 0;

public final static int A_STAR = 1;

public final static int GENETIC = 2;

int dependency_type = RANDOM_DEPENDENCY;

int search_type = GREEDY;

}//END INTERFACE "setupConstants"

;;;; astar search algorithm

(defun set-job-list ()

(let* ((job-list nil))

(dotimes (i *number-of-jobs* job-list)

(setf job-list

(append job-list (list i))))))

(defun set-machine-list ()

(let* ((machine-list nil))

(dotimes (i *number-of-machines* machine-list)

(setf machine-list

(append machine-list (list i))))))

(defun get-time-to-compute (job machine)

(elt (elt *etc-matrix* job) machine))

(defun astarsearch (start input-file output-file)

(read-input-file input-file)

(setf *algorithm-start-time* (get-universal-time))

(setf *schedule* (astarsearch2

(list (list (evalfn start) start)) nil))

(setf *algorithm-stop-time* (get-universal-time))

(write-output-file output-file))

(defun astarsearch2 (agenda usedagenda)

(when agenda

(if

(goalreached (second (first agenda)))

(last (reverse (rest (first agenda))))

(astarsearch2

(merge

'list

(remove-bad-agitems

(mapcar

#'(lambda

(newstate)

(let ((newpath

(cons newstate (rest (first agenda)))))

(cons (+ (evalfn newstate) (costfn newpath))

newpath)))

(successors (second (first agenda))))

(append agenda usedagenda))

(rest agenda)

#'firstlessp)

(cons (first agenda) usedagenda)))))

(defun remove-bad-agitems (agitems oldagitems)

(sort

(remove-if

#'(lambda (agitem)

(some #'(lambda (oldagitem)

(and (>= (first agitem) (first oldagitem))

(equalstate (second agitem) (second oldagitem))))

oldagitems))

agitems)

#'firstlessp))

(defun firstlessp (agitem1 agitem2)

(< (first agitem1) (first agitem2)))

(defun successors (state)

(let* ((immediate-successors (successors2 state))

(complete-successors nil))

(dotimes (i (length immediate-successors) complete-successors)

(setf complete-successors

(append complete-successors

(list (append (elt immediate-successors i) state)))))))

(defun successors2 (state)

(let* ((successors nil)

(jobs-to-schedule (get-jobs-to-schedule state))

(machine-stop-times (get-machine-stop-times state)))

(dotimes (m (length *machines*) successors)

(dotimes (j (length jobs-to-schedule) nil)

(if (dependency-status (elt jobs-to-schedule j)

jobs-to-schedule)

(setf successors

(cons

(list (list (elt jobs-to-schedule j)

(elt *machines* m)

(elt machine-stop-times m)

(+ (elt machine-stop-times m)

(get-time-to-compute (elt jobs-to-schedule j) m))))

successors)))))))

(defun goalreached (statelist)

(if (equalp (length (get-jobs-to-schedule statelist)) 0) t nil))

(defun equalstate (state1 state2)

(equal state1 state2))

(defun costfn (statelist)

(let* ((cost 0)

(machine-cost (get-individual-machine-cost (first statelist))))

(dotimes (n (length machine-cost) cost)

(if (> (elt machine-cost n) cost)

(setf cost (elt machine-cost n))))))

(defun evalfn (statelist)

(if (= (length (get-jobs-to-schedule statelist)) 0) 0

(if (>= (length (get-jobs-to-schedule statelist)) (length *machines*))

(/ (get-unscheduled-job-time statelist) (length *machines*))

(/ (get-unscheduled-job-time statelist) (length (get-jobs-to-schedule statelist))))))

(defun get-jobs-to-schedule (state)

(let* ((jobs-to-schedule *jobs*))

(dotimes (n (length state) jobs-to-schedule)

(if (memberofp (first (elt state n)) jobs-to-schedule)

(setf jobs-to-schedule

(remove (first (elt state n)) jobs-to-schedule))))))

(defun get-average-job-time ()

(let* ((average-job-time (init-job-list)))

(dotimes (i (length *jobs*) average-job-time)

(dotimes (j (length *machines*))

(setf (elt average-job-time i)

(+ (elt average-job-time i)

(get-time-to-compute i j))))

(setf (elt average-job-time i)

(/ (elt average-job-time i) (length *machines*))))))

(defun get-unscheduled-job-time (statelist)

(let* ((time-left 0)

(jobs-remaining (get-jobs-to-schedule statelist)))

(dotimes (n (length jobs-remaining) time-left)

(setf time-left

(+ time-left (elt (get-average-job-time) (elt jobs-remaining n)))))))

(defun get-individual-machine-cost (state)

(let* ((machine-cost (init-machine-list)))

(dotimes (n (length state) machine-cost)

(let* ((machine-to-update (second (elt state n)))

(job-start-time (third (elt state n)))

(job-finish-time (fourth (elt state n)))

(job-scheduled (first (elt state n))))

(setf (elt machine-cost machine-to-update)

(+ (elt machine-cost machine-to-update)

(get-time-to-compute (first (elt state n))

(second (elt state n)))))

(if (> job-finish-time (elt *deadline-matrix* job-scheduled))

(setf (elt machine-cost machine-to-update)

(+ (elt machine-cost machine-to-update)

(- job-finish-time (elt *deadline-matrix* job-scheduled)))))))))

(defun get-machine-stop-times (state)

(let* ((machine-stop-times (init-machine-list)))

(dotimes (i (length state) machine-stop-times)

(let* ((machine (second (elt state i))))

(setf (elt machine-stop-times machine)

(fourth (elt state i)))))))

(defun init-job-list ()

(let* ((average-job-time nil))

(dotimes (i (length *jobs*) average-job-time)

(setf average-job-time

(append '(0) average-job-time)))))

(defun init-machine-list ()

(let* ((machine-cost nil))

(dotimes (i (length *machines*) machine-cost)

(setf machine-cost

(append '(0) machine-cost)))))

(defun notmemberofp (item list)

(let* ((memberstatus t))

(dotimes (n (length list) memberstatus)

(if (equalp item (elt list n))

(setf memberstatus nil)))))

(defun memberofp (item list)

(let* ((memberstatus nil))

(dotimes (n (length list) memberstatus)

(if (equalp item (elt list n))

(setf memberstatus t)))))

(defun read-input-file (filename)

(setq in-stream (open filename :direction :input))

(let* ((number-of-jobs (read in-stream))

(number-of-machines (read in-stream)))

(setf *number-of-jobs* number-of-jobs)

(setf *number-of-machines* number-of-machines)

(setf *jobs* (set-job-list))

(setf *machines* (set-machine-list))

(read-etc-matrix in-stream)

(read-dependency-matrix in-stream)

(read-deadline-matrix in-stream)

(close in-stream)))

(defun read-etc-matrix (in-stream)

(let* ((individual-job-times nil)

(etc-matrix nil))

(dotimes (i *number-of-jobs*)

(setf individual-job-times nil)

(dotimes (j *number-of-machines*)

(setf individual-job-times

(append individual-job-times (list (read in-stream)))))

(setf etc-matrix

(append etc-matrix (list individual-job-times))))

(setf *etc-matrix* etc-matrix)))

(defun read-dependency-matrix (in-stream)

(let* ((individual-job-dependencies nil)

(dependency-matrix nil))

(dotimes (i *number-of-jobs*)

(setf individual-job-dependencies nil)

(dotimes (j *number-of-jobs*)

(setf individual-job-dependencies

(append individual-job-dependencies (list (read in-stream)))))

(setf dependency-matrix

(append dependency-matrix (list individual-job-dependencies))))

(setf *dependency-matrix* dependency-matrix)))

(defun read-deadline-matrix (in-stream)

(let* ((deadline-matrix nil))

(dotimes (i *number-of-jobs*)

(setf deadline-matrix

(append deadline-matrix (list (read in-stream)))))

(setf *deadline-matrix* deadline-matrix)))

(defun write-output-file (filename)

(setq out-stream (open filename :direction :output))

(print 'LISP-A*-Search-Summary out-stream)

(dotimes (i *number-of-jobs*)

(print (elt (first *schedule*) i) out-stream))

(print 'Algorithm-Compute-Time out-stream)

(print (- *algorithm-stop-time* *algorithm-start-time*) out-stream)

(print 'Meta-Task-Completion-Time out-stream)

(print (get-completion-time) out-stream)

(close out-stream))

(defun dependency-status (child-job jobs-to-schedule)

(let* ((status T)

(parent-job nil))

(dotimes (i (length *jobs*) status)

(if (AND (= (elt (elt *dependency-matrix* i) child-job)

(memberofp i jobs-to-schedule))

(setf status NIL)))))

(defun get-completion-time ()

(let* ((max-time 0))

(dotimes (i *number-of-jobs* max-time)

(if (> (fourth (elt (first *schedule*) i)) max-time)

(setf max-time (fourth (elt (first *schedule*) i)))))))

;;;; simulated annealing algorithm

(defun set-job-list ()

(let* ((job-list nil))

(dotimes (i *number-of-jobs* job-list)

(setf job-list

(append job-list (list i))))))

(defun set-machine-list ()

(let* ((machine-list nil))

(dotimes (i *number-of-machines* machine-list)

(setf machine-list

(append machine-list (list i))))))

(defun get-time-to-compute (job machine)

(elt (elt *etc-matrix* job) machine))

(defun astarsearch (start input-file output-file)

(let* ((schedule nil))

(read-input-file input-file)

(setf *algorithm-start-time* (get-universal-time))

(setf schedule (astarsearch2

(list (list (evalfn start) start)) nil))

(setf *algorithm-stop-time* (get-universal-time))

(write-output-file output-file schedule)))

(defun astarsearch2 (agenda usedagenda)

(when agenda

(if

(goalreached (second (first agenda)))

(last (reverse (rest (first agenda))))

(astarsearch2

(merge

'list

(remove-bad-agitems

(mapcar

#'(lambda

(newstate)

(let ((newpath

(cons newstate (rest (elt agenda (get-state-to-visit agenda))))))

(cons (+ (evalfn newstate) (costfn newpath))

newpath)))

(successors (second (elt agenda (get-state-to-visit agenda)))))

(append agenda usedagenda))

(rest agenda)

#'firstlessp)

(cons (first agenda) usedagenda)))))

(defun remove-bad-agitems (agitems oldagitems)

(sort

(remove-if

#'(lambda (agitem)

(some #'(lambda (oldagitem)

(and (>= (first agitem) (first oldagitem))

(equalstate (second agitem) (second oldagitem))))

oldagitems))

agitems)

#'firstlessp))

(defun firstlessp (agitem1 agitem2)

(< (first agitem1) (first agitem2)))

(defun successors (state)

(let* ((immediate-successors (successors2 state))

(complete-successors nil))

(dotimes (i (length immediate-successors) complete-successors)

(setf complete-successors

(append complete-successors

(list (append (elt immediate-successors i) state)))))))

(defun successors2 (state)

(let* ((successors nil)

(jobs-to-schedule (get-jobs-to-schedule state))

(machine-stop-times (get-machine-stop-times state)))

(dotimes (m (length *machines*) successors)

(dotimes (j (length jobs-to-schedule) nil)

(if (dependency-status (elt jobs-to-schedule j)

jobs-to-schedule)

(setf successors

(cons

(list (list (elt jobs-to-schedule j)

(elt *machines* m)

(elt machine-stop-times m)

(+ (elt machine-stop-times m)

(get-time-to-compute (elt jobs-to-schedule j) m))))

successors)))))))

(defun goalreached (statelist)

(if (equalp (length (get-jobs-to-schedule statelist)) 0) t nil))

(defun equalstate (state1 state2)

(equal state1 state2))

(defun costfn (statelist)

(let* ((cost 0)

(machine-cost (get-individual-machine-cost (first statelist))))

(dotimes (n (length machine-cost) cost)

(if (> (elt machine-cost n) cost)

(setf cost (elt machine-cost n))))))

(defun evalfn (statelist)

(if (= (length (get-jobs-to-schedule statelist)) 0) 0

(if (>= (length (get-jobs-to-schedule statelist)) (length *machines*))

(/ (get-unscheduled-job-time statelist) (length *machines*))

(/ (get-unscheduled-job-time statelist) (length (get-jobs-to-schedule statelist))))))

(defun get-jobs-to-schedule (state)

(let* ((jobs-to-schedule *jobs*))

(dotimes (n (length state) jobs-to-schedule)

(if (memberofp (first (elt state n)) jobs-to-schedule)

(setf jobs-to-schedule

(remove (first (elt state n)) jobs-to-schedule))))))

(defun get-average-job-time ()

(let* ((average-job-time (init-job-list)))

(dotimes (i (length *jobs*) average-job-time)

(dotimes (j (length *machines*))

(setf (elt average-job-time i)

(+ (elt average-job-time i)

(get-time-to-compute i j))))

(setf (elt average-job-time i)

(/ (elt average-job-time i) (length *machines*))))))

(defun get-unscheduled-job-time (statelist)

(let* ((time-left 0)

(jobs-remaining (get-jobs-to-schedule statelist)))

(dotimes (n (length jobs-remaining) time-left)

(setf time-left

(+ time-left (elt (get-average-job-time) (elt jobs-remaining n)))))))

(defun get-individual-machine-cost (state)

(let* ((machine-cost (init-machine-list)))

(dotimes (n (length state) machine-cost)

(let* ((machine-to-update (second (elt state n)))

(job-start-time (third (elt state n)))

(job-finish-time (fourth (elt state n)))

(job-scheduled (first (elt state n))))

(setf (elt machine-cost machine-to-update)

(+ (elt machine-cost machine-to-update)

(get-time-to-compute (first (elt state n))

(second (elt state n)))))

(if (> job-finish-time (elt *deadline-matrix* job-scheduled))

(setf (elt machine-cost machine-to-update)

(+ (elt machine-cost machine-to-update)

(- job-finish-time (elt *deadline-matrix* job-scheduled)))))))))

(defun get-machine-stop-times (state)

(let* ((machine-stop-times (init-machine-list)))

(dotimes (i (length state) machine-stop-times)

(let* ((machine (second (elt state i))))

(setf (elt machine-stop-times machine)

(fourth (elt state i)))))))

(defun init-job-list ()

(let* ((average-job-time nil))

(dotimes (i (length *jobs*) average-job-time)

(setf average-job-time

(append '(0) average-job-time)))))

(defun init-machine-list ()

(let* ((machine-cost nil))

(dotimes (i (length *machines*) machine-cost)

(setf machine-cost

(append '(0) machine-cost)))))

(defun notmemberofp (item list)

(let* ((memberstatus t))

(dotimes (n (length list) memberstatus)

(if (equalp item (elt list n))

(setf memberstatus nil)))))

(defun memberofp (item list)

(let* ((memberstatus nil))

(dotimes (n (length list) memberstatus)

(if (equalp item (elt list n))

(setf memberstatus t)))))

(defun read-input-file (filename)

(setq in-stream (open filename :direction :input))

(let* ((number-of-jobs (read in-stream))

(number-of-machines (read in-stream)))

(setf *number-of-jobs* number-of-jobs)

(setf *number-of-machines* number-of-machines)

(setf *jobs* (set-job-list))

(setf *machines* (set-machine-list))

(read-etc-matrix in-stream)

(read-dependency-matrix in-stream)

(read-deadline-matrix in-stream)

(close in-stream)))

(defun read-etc-matrix (in-stream)

(let* ((individual-job-times nil)

(etc-matrix nil))

(dotimes (i *number-of-jobs*)

(setf individual-job-times nil)

(dotimes (j *number-of-machines*)

(setf individual-job-times

(append individual-job-times (list (read in-stream)))))

(setf etc-matrix

(append etc-matrix (list individual-job-times))))

(setf *etc-matrix* etc-matrix)))

(defun read-dependency-matrix (in-stream)

(let* ((individual-job-dependencies nil)

(dependency-matrix nil))

(dotimes (i *number-of-jobs*)

(setf individual-job-dependencies nil)

(dotimes (j *number-of-jobs*)

(setf individual-job-dependencies

(append individual-job-dependencies (list (read in-stream)))))

(setf dependency-matrix

(append dependency-matrix (list individual-job-dependencies))))

(setf *dependency-matrix* dependency-matrix)))

(defun read-deadline-matrix (in-stream)

(let* ((deadline-matrix nil))

(dotimes (i *number-of-jobs*)

(setf deadline-matrix

(append deadline-matrix (list (read in-stream)))))

(setf *deadline-matrix* deadline-matrix)))

(defun write-output-file (filename schedule)

(setq out-stream (open filename :direction :output))

(print 'LISP-Simulated-Annealing-Search-Summary out-stream)

(dotimes (i *number-of-jobs*)

(print (elt (first schedule) i) out-stream))

(print 'Algorithm-Compute-Time out-stream)

(print (- *algorithm-stop-time* *algorithm-start-time*) out-stream)

(close out-stream))

(defun dependency-status (child-job jobs-to-schedule)

(let* ((status T)

(parent-job nil))

(dotimes (i (length *jobs*) status)

(if (AND (= (elt (elt *dependency-matrix* i) child-job)

(memberofp i jobs-to-schedule))

(setf status NIL)))))

(defun get-state-to-visit (agenda)

(let* ((original-cost-list nil)

(denominator 0)

(weighted-cost-list nil)

(normalized-cost-list nil)

(probability-window-list '(0))

(state-to-visit nil)

(sum 0))

(setf original-cost-list (get-original-cost-list agenda))

(setf denominator (get-denominator original-cost-list))

(setf weighted-cost-list (get-weighted-cost-list original-cost-list))

(setf annealed-cost-list (get-annealed-cost-list weighted-cost-list))

(setf normalized-cost-list (get-normalized-cost-list annealed-cost-list denominator))

(setf probability-window-list (get-probability-window-list normalized-cost-list))

(setf state-to-visit (get-state-to-visit2 probability-window-list))

(setf sum (get-sum normalized-cost-list))

(print 'weighted)

(print weighted-cost-list)

(print 'annealed)

(print annealed-cost-list)

(print 'normalized)

(print normalized-cost-list)

(print 'sum)

(print sum)

(print 'probability)

(print probability-window-list)

(print 'agenda-length)

(print (length agenda))

(print 'state-to-visit)

(print state-to-visit)))

(defun get-original-cost-list (agenda)

(let* ((original-cost-list nil))

(dotimes (i (length agenda) original-cost-list)

(setf original-cost-list

(append original-cost-list

(list (first (elt agenda i))))))))

(defun get-denominator (original-cost-list)

(let* ((denominator 0))

(dotimes (i (length original-cost-list) denominator)

(setf denominator

(+ denominator (/ (first original-cost-list) (elt original-cost-list i)))))))

(defun get-weighted-cost-list (original-cost-list)

(let* ((weighted-cost-list nil))

(dotimes (i (length original-cost-list) weighted-cost-list)

(setf weighted-cost-list

(append weighted-cost-list

(list (/ (first original-cost-list) (elt original-cost-list i))))))))

(defun get-annealed-cost-list (weighted-cost-list)

(let* ((annealed-cost-list nil)

(annealing-factor (get-annealing-factor)))

(if (< annealing-factor 1)

(setf annealing-factor 1))

(print 'annealing-factor)

(print annealing-factor)

(dotimes (i (length weighted-cost-list) annealed-cost-list)

(if (= i 0)

(setf annealed-cost-list (list (first weighted-cost-list)))

(setf annealed-cost-list

(append annealed-cost-list

(list (/ (elt weighted-cost-list i) annealing-factor))))))))

(defun get-normalized-cost-list (annealed-cost-list denominator)

(let* ((normalized-cost-list nil))

(dotimes (i (length annealed-cost-list) normalized-cost-list)

(setf normalized-cost-list

(append normalized-cost-list

(list (/ (elt annealed-cost-list i) denominator)))))))

(defun get-probability-window-list (normalized-cost-list)

(let* ((probability-window-list '(0)))

(dotimes (i (length normalized-cost-list) probability-window-list)

(if (= i 0)

(setf probability-window-list

(append probability-window-list

(list (first normalized-cost-list))))

(setf probability-window-list

(append probability-window-list

(list (+ (elt normalized-cost-list i)

(elt probability-window-list i)))))))))

(defun get-state-to-visit2 (probability-window-list)

(let* ((random-selector (random (float 1)))

(state-to-visit nil))

(print random-selector)

(dotimes (i (- (length probability-window-list) 1) state-to-visit)

(if

(AND (if (> random-selector (elt probability-window-list i)) t)

(if (< random-selector (elt probability-window-list (+ i 1))) t))

(setf state-to-visit i)))))

(defun get-sum (normalized-cost-list)

(let* ((sum 0))

(dotimes (i (length normalized-cost-list) sum)

(setf sum

(+ sum (elt normalized-cost-list i))))))

(defun get-annealing-factor ()

(let* ((scaling-factor 1))

(* scaling-factor

(- (get-universal-time) *algorithm-start-time*))))

THIS PAGE INTENTIONALLY LEFT BLANK

LIST OF REFERENCES

[ALHUSAINI99] Ammar Alhusaini, Viktor Prasanna, and C.S. Raghavendra. A Unified Resource Scheduling Framework for heterogeneous Computing Environments. Proc. 8th IEEE Heterogeneous Computing Workshop, Puerto Rico, April 1999.

[ALI94] Hesham H. Ali, Theodore G. Lewis, and Hesham El-Rewini. Task Scheduling in Parallel and Distributed Systems. Prentice Hall, 1994.

[ARMSTRONG98] Robert Armstrong, Debra Hensgen, and Taylor Kidd, The Relative Performance of Various Mapping Algorithms is Independent of Sizable Variances in Run-time Predictions, 7th Heterogenous Computing Workshop (HCW'98), Mar. 1998, pp. 79-87.

[BHARADWAJ96] Veeravalli Bharadwaj, Debasish Ghose, Venkatarman Mani, and Thomas G. Robertazzi. Scheduling Divisible Loads in Parallel and Distributed Systems. IEEE Computer Society Press, 1996.

[BHAT99] Prashanth B. Bhat, C.S. Raghavendra, and Viktor K. Prasanna. Efficient Collective Communication in Distributed Heterogeneous Systems. The 19th International Conference on Distributed Computing Systems (ICDCS), 1999.

[CORMEN97] Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to Algorithms. The MIT Press, 1997.

[FREUND98] Richard F. Freund, Michael Gherrity, Stephen Ambrosius, Mark Campbell, Mike Halderman, Debra Hensgen, Elaine Keith, Taylor Kidd, Matt Kussow, John D. Lima, Francesca Mirabile, Lantz Moore, Brad Rust,and Howard Jay Siegel, Scheduling Resources in Multi-User, Heterogeneous, Computing Environments with SmartNet, 7th Heterogeneous Computing Workshop (HCW '98), Orlando, FL, Mar. 1998, pp. 184-199.

[GALLI00] Doreen L. Galli. Distributed Operating Systems Concepts and Practice. Prentice Hall, 2000.

[HURSON95] Ali Hurson, Krishna Kavi, and Behrooz Shirazi. Scheduling and Load Balancing in Parallel and Distributed Systems. IEEE Computer Society Press, 1995.

[KIDD96] Taylor Kidd, Debra Hensgen, Richard Freund, and Lantz Moore, SmartNet: A Scheduling Framework for Heterogeneous Computing, proceedings of the International symposium on Parallel Architectures, Algorithms, and Networks (I-SPAN'96), sponsored by the IEEE computer Society, Beijing, China, Jun. 1996, pp. 514-521.

[LUGER89] George F. Luger and William A. Stubblefield. Artificial Intelligence and the Design of Expert Systems. The Benjamin/Cummings Publishing Company, Inc., 1989.

[MSHN00] Management Systems for Heterogeneous Networks World Wide Web Page: http://www.mshn.org/

BIBLIOGRAPHY

[ALI99] Shoukat Ali, A Comparative Study of Dynamic Mapping Heuristics for a Class of Independent Tasks onto Heterogeneous Computing Systems, Master's Thesis, School of Electrical and Computer Engineering, Purdue University, 1999.

[ARMSTRONG97] Robert Armstrong. Investigation of Effect of Different Run-Time Distributions on Smartnet Performance. Masters Thesis, Naval Postgraduate School, Monterey, CA, Sep. 1997. Debra Hensgen, advisor, Taylor Kidd, co-advisor.

[BRAUN99] Tracy D. Braun, Howard Jay Siegel, Noah Beck, Ladislau L. Boloni, Muthucumaru Maheswaran, Albert I. Reuther, James P. Robertson, Mitchell D. Theys, Bin Yao, Debra Hensgen, and Richard F. Freund, A Comparison Study of Static Mapping Heuristics for a Class of Meta-tasks on Heterogeneous Computing Systems, Proceedings of the 8th IEEE Workshop on Heterogeneous Computing Systems (HCW '99), San Juan, Puerto Rico, Apr. 1999.

[BRAUN98] Tracy D. Braun, Muthucumaru Maheswaran, Howard Jay Siegel, Noah Beck, Ladislau Boloni, Albert I. Reuther, James P. Robertson, Mitchell D. Theys, and Bin Yao, A Taxonomy for Describing Matching and Scheduling Heuristics for Mixed-Machine Heterogeneous Computing Systems, Workshop on Advances in Parallel and Distributed Systems (in proceedings of the IEEE Symposium on Reliable Distributed Systems, Oct. 1998, pp. 330-335), West Lafayette, IN, Oct. 1998.

[KRUATRACHUE87] Boontee Kruatrachue, Static Task Scheduling and Grain Packing in Parallel Processing Systems, PhD Thesis, School of Electrical and Computer Engineering, University of Michigan, 1987.

[KWOK99] Yu-Kwong Kwok, Anthony A. Maciejewski, Howard Jay Siegel, Arif Ghafoor, and Ishfaq Ahmad, Evaluation of A Semi-Static Approach to Mapping Dynamic Iterative Tasks onto Heterogeneous Computing Systems, 1999 International Symposium on Parallel Architectures, Algorithms, and Networks (I-SPAN '99), pp. 204-209, Fremantle, Australia, June 1999.

[MAHESWARAN98] Muthucumaru Maheswaran, Tracy Braun, and Howard Jay Siegel, High-Performance Mixed-Machine Heterogeneous Computing, 6th Euromicro Workshop on Parallel and Distributed Processing, Madrid, Spain, Jan. 1998, pp. 3-9.

[MAHESWARAN98] Muthucumaru Maheswaran and Howard Jay Siegel, A Dynamic Matching and Scheduling Algorithm for Heterogeneous Computing Systems, 7th Heterogeneous Computing Workshop (HCW '98), Orlando, FL, Mar. 1998, pp. 57-69.

[MAHESWARAN 99] Muthucumaru Maheswaran, Shoukat Ali, Howard Jay Siegel, Debra Hensgen, and Richard F. Freund, Dynamic Mapping of a Class of Independent Tasks onto Heterogeneous Computing Systems, Journal of Parallel and Distributed Computing, Special Issue on Software Support for Distributed Computing, 1999, accepted and scheduled to appear.

[MAHESWARAN99] Muthucumaru Maheswaran, Tracy D. Braun, and Howard Jay Siegel, Heterogeneous Distributed Computing, Encyclopedia of Electrical and Electronics Engineering, J. G. Webster, editor, John Wiley & Sons, New York, NY, 1999, Vol 8, pp. 679-690.

[MAHESWARAN99] Muthucumaru Maheswaran, Shoukat Ali, Howard Jay Siegel, Debra Hensgen, and Richard F. Freund, Dynamic Matching and Scheduling of a Class of Independent Tasks onto Heterogeneous Computing Systems, proceedings of the 8th Workshop on Heterogeneous Computing Systems (HCW '99), San Juan, Puerto Rico, Apr. 1999.

[MITCHELL96] Melanie Mitchell. An Introduction to Genetic Algorithms. The MIT Press, 1996.

[ROSEN92] Benjamin Rosen. Advances in Optimization and Parallel Computing. North-Holland, 1992.

[WANG97] Lee Wang, Howard Jay Siegel, Vwani P. Roychowdhury, and Anthony A. Maciejewski, Task Matching and Scheduling in Heterogeneous Computing Environments Using a Genetic-Algorithm-Based Approach, Journal of Parallel and Distributed Computing, Special Issue on Parallel Evolutionary Computing, Vol. 47, No. 1, Nov. 1997, pp. 8-22.

INITIAL DISTRIBUTION LIST

Defense Technical Information Center 2

8725 John J. Kingman Road, Suite 0944

Ft. Belvoir, VA 22060-6218
Dudley Knox Library 2

Naval Postgraduate School

411 Dyer Road

Monterey, CA 93943-5101
Professor Neil Rowe 2

Computer Science Department, Code 32

Naval Postgraduate School

Monterey, CA 93943-5101
Michael D. Niedert 2

3908 Knoll Ridge Drive

Cedar Falls, Iowa 50613