Robust Recognition of Ship Types from an Infrared Silhouette
Jorge Alves, Jessica Herman, and Neil C. Rowe
U.S. Naval Postgraduate School
Code CS/Rp, 833 Dyer Road
Monterey, CA USA 93943
ncrowe@nps.navy.mil
ABSTRACT
Accurate identification of unknown contacts crucial in military intelligence. Automated systems that quickly and accurately determine the identity of a contact could be a benefit in backing up electronic-signals identification methods. This work reports two experimental systems for ship classification from infrared FLIR images. In an edge-histogram approach, we used the histogram of the binned distribution of observed straight edge segments of the ship image. Some simple tests had a classification success rate of 80% on silhouettes. In a more comprehensive neural-network approach, we calculated scale-invariant moments of a silhouette and used them as input to a neural network. We trained the network on several thousand perspectives of a wire-frame model of the outline of each of five ship classes. We obtained 70% accuracy with detailed tested on real infrared images but performance was more robust than with the edge-histogram approach.
This paper appeared in the Command and Control Research and Technology Symposium, San Diego, CA, June 2004.
I. INTRODUCTION
Autonomous recognition of ships can provide better tracking and automatic monitoring to reduce accidents. Recent advanced in FLIR infrared imaging technology in the U.S. Navy improves its ability to see ships at night, but it is still militarily desirable to remain as far as possible from potential enemy ships, and ships can be observed from any angle. Fortunately, previous tracking data can often considerably reduce the set of possible nearby ships so just a rough classification will suffice to confirm its identity. So this work addresses model-based classification of ships by type from noisy images assuming only a small set of ships are known to be in the vicinity. Figure 1 shows example FLIR input that we used, where darker areas are more radiant.
 |
|
Both local and global methods have been explored for automatic visual object recognition (to be distinguished from object detection, which suggests different methods). Local methods use features such as critical points (Freeman, 1978) or high-resolution pursuit (Jaggi et al, 1999). Systems using local features can perform well in the presence of noise, distortion, or partial occlusion because only one distinctive part need be recognized. However, the distinctive local features of ships are often narrow and searching for them could be computationally intensive.
Global methods include Fourier descriptors (Richard and Hemani, 1974), moments (Teh, 1988), and autoregressive models (Kashyap and Chellapa, 1981). Classic work by Dudani et al (1977) used moment invariants for classification of airplanes. This used six aircraft types and the images were based on physical models. The training set was based on over 3000 images taken in a 140o by 90o sector. The testing set contained 132 images (22 images of each of the six classes) obtained at random viewing aspects. The classification accuracy achieved in this six-class problem was 95%. Reeves et al (1988) improved on this by using "standard moments" on similar data and obtained a best classification result of 93%.
It is unclear how well the work on aircraft classification extends to ships, as ships are mainly distinguishable in small features. Most work has been done on radar images, and a variety of approaches have been tried with no clear consensus. Musman et al (1996) classified ships using local features of radar images, with wire-frame models of ship types, but claims the images were very different from visual ones. Gibbins et al (1999) classified radar images of ships in using global features but their accuracy is so far unimpressive. Gouaillier and Gagnon (1997) classified radar images using principal-component global features and similarity matching to prototypical ships for each ship type to obtain promising results. Alippi (1995) used neural networks applied directly to the image pixels. Lesage and Gagnon used morphological analysis of the object boundary. Additional work on ship classification has been done with synthetic aperture radar when it is important to determine the motion of the object, as in Valin et al (1999) and Yuan and Casasent (2002).
Radar images are often undesirable in military applications because they reveal the location of the imaging system as well as requiring a relatively near viewing distance. So we explore here infrared images of ships which are generally more consistent than radar images and for which it is easier to compensate for environmental effects (McLenaghan and Moore, 1988). Casasent et al (1981) and Zvolanek (1981) used moments of infrared images to classify ships, but their experiments were minimal. Withagen et al (1999) used 32 features including moments and either a simple linear model, a simple quadratic model, or nearest-neighbor matching to prototypes of each of six classes, and they showed promising results on 200 images.
II. AN EDGE-HISTOGRAM APPROACH
The first approach we tried for ship identification focused on the edges of the silhouette of the ship (Herman, 2000). Earlier work (Bizer, 1989) developed a method for identifying ships based on the decomposition of “bumps” on the silhouettes of their decks, inspired by the way Navy personnel are taught to differentiate ship classes. Each class is defined by the structures it contains and their arrangement on the deck. Silhouettes obtained from (Jane's, 1986) were searched for locations where the outline made an upward turn. Each of the areas defined by such turns was further analyzed in the same way in order to develop a model of the whole bump. Finally, the model was identified using a rule-based system. The program found and classified the protrusions with an average accuracy of 78%. The usefulness of this method is restricted, however, by its dependence on detailed, clear silhouettes. A noisy image, or one in which the edge of the ship was not continuous, could not be successfully processed. The time and space required to identify even these few features also limits the scalability of the technique.
A possible solution with noisy images is to apply the Hough transform to detect patterns of broken or intermittent straight lines (Chau and Siu, 1999) distinctive of each ship type. But calculations on the raw Hough transform are difficult and computationally expensive to extend to complex shapes, especially in noisy images with varying scale, translation and rotation. Additionally, since we are trying to classify a ship rather than to find a known shape, a costly matching process would have to be done for each possible ship type. However, the Hough transform still ought to have a role to play in local analysis of image features since straight edges are such important clues in ship identification.
Our approach was to combine some of the standard techniques for recognition in new ways. To locate the ship in the image, we used edge detection, thresholding, and our prior knowledge of the domain. We extracted line segments by applying knowledge of Hough transform space features to our edge image. In the classification stage, we calculated moments and other statistical features both on line segments and directly on image pixels. By employing different methods on different tasks, we hoped to come up with a better solution than any individual process could provide.
OBTAINING AND PREPROCESSING THE DATA
We used a video capture card to obtain frames from footage taken by the crew of a SH-60B Rapid Deployment Kit equipped helicopter. The AN/AAS-44V FLIR is mounted on a springboard at the nose of the aircraft. Our program operates on images captured from FLIR video using a Studio PCTV. This system returns a 320 x 240 pixel TIFF format color image. The program’s second input argument is a database which contains the comparison information for each possible ship class.
Because we used real FLIR images as our data, we dealt with a number of challenges in the preprocessing phase. We limited our samples to pictures in which the entire ship was visible and centered, and only used near-broadside views. Even with these requirements, the scale, position, and orientation of the ship varied significantly between images. The quality of the images was not ideal; we employed techniques to eliminate as much noise and background information from our samples as possible. But to be cost-effective, an automated identification system needs to be able to operate on noisy data.
Our images also contained artifacts of the FLIR system from which they were obtained. The system projects video information and targeting aids onto the screen as shown in Figure 1. These may partially obscure the image and interfere with the identification process. We tested the efficacy of a number of methods in removing these factors.
The FLIR camera can be operated in a number of modes. It can display either black-hot (higher energy areas are black) or white-hot images, and provides both digital and optical zoom capabilities. We chose to use only black-hot images because we can more effectively remove system artifacts from them than from white-hot images. We also decided not to allow images produced with the digital zoom option, as it amplifies background noise significantly.
The program returns a list of the ships in the database that are closest to the unknown ship. Each potential classification has a confidence rating which represents how similar the test image is to that class. We list multiple possibilities because if the test image is very close to more than one database class, we want the system user to be aware of all strong possibilities. When available as with the MARKS system, data from the emitter and ship positioning systems will further narrow the database of candidate classes.
Using straight-line segments as our basic features fit well with our design objectives. Ship images consist mainly of straight lines, so most of the important information in our images is preserved. A line segment can also be represented succinctly by a few numbers: The coordinates of the center, the orientation, and the length fully describe it. This choice even helped us to reduce the noise in the images, as natural noise rarely produces straight lines as long and strong as those found in man-made objects.
IMPLEMENTATION
We implemented our program in MATLAB using the Image Processing Toolbox. During preprocessing we smoothed the images using standard median filtering on 3-by-3 pixel neighborhoods. Filtering reduced the graininess of the images so that fewer false edges were detected in the next step of segmentation. The segmentation process itself eliminated many small regions of the image that resulted from noise, as we only dealt with line segments of significant length.
We applied the rest of our methods after segmentation. Our limitation to black-hot images allowed us to remove all lines from the segmented images which mapped to light areas in the original images. Since the heat generated in the engines ensured that the ship would always be hot relative to the surrounding water, anything light in color must be noise. We automatically generated a mask for each image to represent those pixels with light values, and removed those segments whose centers were within the mask from the edge image. This step also removed some of the processing artifacts, which were generally light. To deal with any that remained, we created another binary image that marked all of the areas where we knew such artifacts would be located. Then, as above, we disregarded all line segments that fell within those regions. Figures 2 and 3 show these processing steps being applied to Figure 1.
We tested and discarded a few other techniques for the removal of spurious edges. Neighborhood averaging of light-colored pixels in the original intensity image did not accomplish anything useful. We tried smoothing areas that were part of a similar mask to the one discussed above, also without success. Finally, we tried to subtract the mask from the edge image before the segmentation step, with the result that we were unable to detect many key segments. Since none of our attempts to clean up the images before segmentation were successful, we were forced to apply the post-processing techniques discussed above. Fortunately, the impact on program efficiency was minimal.

Figure 2: The Figure 1 image after cleanup and edge finding.

Figure 3: The Figure 1 image after further cleanup.
Feature Extraction
After converting an image to grayscale and smoothing it, we searched for strong candidate line segments to use in classification. First, we ran the image through an edge detector. We chose the Canny method because it successfully found all of the important features in our images. We allowed MATLAB to automatically select the threshold for deciding whether or not a value change was significant. To connect intermittent lines, we used a modified version of the robust segment-finding code from (Rowe and Grewe, 2001). This technique used the Hough transform to detect straight lines.
When we had this information, we could find pixels on the lines corresponding to each peak, and connect pixels using the angle defined by the transform results. For each peak, we collected all of the pixels that we reached by simply looking for the next one nearby and at the correct angle. Each of these sets approximated a line segment. We ran this process twice, first with a higher threshold to extract major lines, and then again with a lower threshold to find smaller segments from the pixels which were not matched in the first pass. After this step, we had an image made up of numbered straight-line segments and a list of the endpoints, orientations, and lengths of each segment.
When all of the segments had been located, we applied the delayed preprocessing methods described above to eliminate spurious edges caused by noise or FLIR projection information. This cleaned up both the image and the segment list. As part of this phase, we also determined the center coordinates of each segment, which we used later for statistical calculations. Next, we checked the orientation of the ship in the image to see if we ought to realign it. We used the Hough transform for this step as well. Since the highest peak in transform space usually is the bottom of the ship because the waterline creates a strong straight edge, we looked at the orientation of that line and rotated the image to make it horizontal.
Finally, we removed any line segments on the edges of the image, as they are unlikely to be part of the ship and would interfere with our statistics. We found the y-axis standard deviation of edge pixels, and simply removed any line segments that fell more than two and a half standard deviations from the image’s y-axis mean. The resulting binary image showed the important features of the ship with very few confounding factors.
Feature Analysis
To ensure scale independence, translation independence, and some degree of noise independence for image analysis, we found the median and standard deviation of pixel locations for both x- and y-axes. Using this, twenty-five rectangular areas in the image were defined. The width of each area was one standard deviation as calculated along the x-axis, and the height was one standard deviation along the y-axis. We centered the first rectangle on the median image pixel, then added two more rows and columns in every direction, as shown in Figure 4.
For each of these subranges, we counted the fraction of the total edge pixels. These measures gave a five-by-five array of fractions that showed how the pixels were distributed and thus gave the approximate shape of the ship. Next, we totaled the pixels in each box based on orientation. We defined four angle ranges, and for each area, counted the number of pixels which belonged to line segments in each angle range. Again, we divided the results by the total number of image edge pixels. This step resulted in a five-by-five-by-four array. We also calculated the third moment of the image pixel locations about the mean in the x and y directions. This feature measures skew or asymmetry, so it was helpful in distinguishing ship classes such as tankers and destroyers. The final form of our feature vector consisted of the two distribution arrays and the moment value, and contained a total of 126 elements.
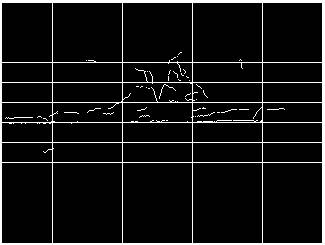
Figure 4: Binning of edge segments for edge histogram.
Then to compare two segmented images, we summed the absolute values of the differences between corresponding features of the two images. We used feature weights of 1, 10 and 5 for the pixel distribution, pixel orientation, and moment differences. These weights were chosen subjectively. The smaller the weighted sum of the absolute differences, the more alike the two images were judged.
RESULTS
We had a limited set of FLIR images for use in our tests. Consequently, we were not able to experiment with many different ship classes. Some of the images we did receive were too poor in quality to give good results. Our better images were of Arleigh Burke class destroyers and aircraft carriers. We had nine images of Arleigh Burkes and six images of carriers. Within those sets, the images varied enough to make identification difficult. In order to have more variety in our comparisons, we included two pictures of Spruance class destroyers in which the ships were small, as well as one very noisy picture of an Iranian PTG patrol craft.
Out of the fifteen images that were of reasonably good quality (the Arleigh Burkes and the carriers), eleven (73%) were most similar to another ship in their class. When the class differences were averaged, however, thirteen of the fifteen (87%) were on average more similar to ships in the class to which they belonged. This result suggested that when we constructed a database to store data for multiple ship classes, we should average similarities over many views of the same ship class to classify a ship.
For another test, we tried a "case-based reasoning" approach. We selected one image from each ship class to put in the database. We chose the images that minimized the average difference to the rest of the ships in their class, using the calculations of the previous test. All of the remaining images were then compared to these exemplars. Of the thirteen remaining good images (not counting the Spruance), two Arleigh Burkes and one carrier were incorrectly identified in this test, for a success rate of 77%. Since this was lower than the success rate when we averaged the class values, we tried a new strategy.
We constructed feature vectors that were the average of the features over all images in each class with the exception of two test images. We then tested these two images against the vector averages. Of our fifteen test images (we only counted each carrier image once even though we compared some of them twice), twelve (80%) were correctly identified. One of the mismatches, however, was with the Spruance class; since there were only two images in that group and neither was very good, that test was somewhat unfair. Ignoring it, the percentage of accurate classifications between Arleigh Burkes and aircraft carriers was twelve of fourteen, or 89%.
The most time-consuming portion of our program by far was the extraction of features from the original images. Each image required approximately 55 seconds for this step
Constructing a big image-feature database will therefore be a lengthy process. Since the database can be put together offline, this is not a major concern; what matters more is the program’s speed in recognition mode. When making 50 image-pair comparisons, the total time was less than one second, and for 100 comparisons, the time was still under three seconds. Thus a single comparison takes around three hundredths of a second. Execution time could be reduced significantly by running our code on a faster computer. Translating our MATLAB code into a more efficient language would also give us a speed advantage.
III. A NEURAL NETWORK APPROACH
METHODS
Our second approach used detailed geometric models of ship types, moment invariants, and a neural network (Alves, 2001). A particular open question we investigated was whether performance can be enhanced by using a neural network to recognize subtle differences in global features. Neural networks have been successfully applied to many image-classification problems (Perantonis and Lisboa, 1992; Rogers et al, 1990). Neural networks can run fast, can examine many competing hypotheses simultaneously, can perform well with noise and distortion, and can avoid local minima unlike variants of Newton’s method for optimization. Model-based object recognition using neural networks seems attractive because the complexity and the computational burden increase slowly as the number of models increases. Training time is not a problem for our application since ships change slowly and retraining will rarely be needed. Neural networks also represent a more generalizable solution than the 32 carefully-chosen problem-specific features of Withagen et al (1999) and represent significantly more classification power than the simple classification methods (nearest-neighbor, linear classifier, and quadratic classifier) used in that work. Furthermore, with them we can eliminate the four required assumptions made in Withagen et al: The ships identified do not need to be known, their height and distance do not need to be known, and more than one aspect angle need not be acquired.
Moment invariants are a reliable way to construct a feature vector of low dimension for a classifier of two-dimensional patterns. Using nonlinear combinations of normalized central moments, (Hu, 1962) derived seven metrics invariant under image translation, scaling and rotation. These can be computed for both a shape boundary and a region. Details such as the stacks of a ship are better characterized by the boundary; large structural features of the ship are better characterized by the region. We used six moments from the silhouette boundary and six from the region; as the distance of the object in the image was not known, the M1’ component was not used. We made those twelve parameters (features) the inputs to a neural network trained with backpropagation.
To obtain training data, five ship types were modeled: an aircraft carrier, a frigate, a destroyer, a research ship, and a merchant ship (a tanker). With these, it was possible to address a typical scenario at sea with military ships, small civilian ships, and big merchant ships. Three-dimensional wire-frame models represented the types, requiring a total of 443 vertices and 247 polygons (see Figure 5). The models were based on scaled drawings of representative ships of each type and required careful manual design since no geometric models were available. Note that these were models of ship types, not individual ships, and were designed to reflect only features common to all ships in the type.
Azimuth was measured counterclockwise of the viewpoint in the horizontal plane, and elevation was measured as inclination downward from horizontal. The origin was located at the center of gravity of the ship model, using only the portion above sea level. The five models are shown in Figure 5 for azimuth angle of –37.5 degrees and the elevation angle of 30 degrees. We create silhouettes of these models through orthographic projection since generally ships are far away in military applications.
 |

|
For test input, we used the three hours of video taken at sea mentioned above. The video showed a few other small boats, but only images of our ship types were considered for analysis. We selected 25 representative frames (each 320 by 240 pixels) for testing: two destroyer images, two aircraft carriers, 15 merchant ships, and four research ships. Image frames were acquired as before using a commercial video-grabber board installed in a PC desktop computer.
The infrared system projects alphanumeric data and targeting aids onto the screen so prefiltering was necessary to remove them. (Figure 1 showed an example input image.) The brightness histogram for these images consistently had three peaks corresponding to water, sky, and ship (see Figure 6), so we segmented pixels into categories using the minima between the peaks. We then changed pixels inconsistent with all their neighbors to be consistent. This produced a cleaner output than with the preprocessing of earlier edge-histogram approach (Figure 7).
The neural-network classifier required training with representative silhouettes to maximize performance. (Although human judgement may help training (Ornes and Sklansky, 1997), military needs usually require fully automated training.) Symmetric three-dimensional objects like ships can have azimuth restricted to a range of 180o. Elevation angles were limited to 0o to 45o since we addressed broadside views only in this work, as on the surface of the ocean or in a helicopter from some distance away. Figure 8 shows a few representative example silhouettes created for a single ship model that were used in training.
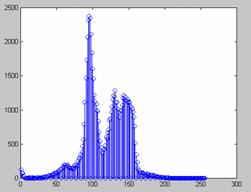
Figure 6: Histogram of image brightnesses, useful for thresholding.
Figure 7: Ship image after cleanup.
Figure 8: Example silhouettes of a single ship that were used in training the neural network.
RESULTS
We implemented our approach in the Matlab programming language and tested it. Experiments measured the fraction of correct identifications in all views of that kind of ship (recall) and the fraction of correct identifications in all identifications (precision). We examined performance when no elevation or azimuth information is known about the image viewpoint, although course-tracking data in the real world may permit many possible viewpoints to be ruled out and thus improve on the results given here.
We first experimented with a network with 12 input nodes, 20 hidden nodes, and 5 output nodes. We trained it with 240 images representing 15-degree increments in azimuth and four viewing angles of 0o, 15o, 30o and 45o. This network had 90.1% recall on evenly spaced test data after training. But significant errors occurred at high azimuth angles. So we used a closer spacing of training cases where the program had difficulty, with azimuth angles of -90, -85, -80, -75, -70, -65, -60, -55, -50, -45, -30, -15, 0, 15, 30, 45, 50, 55, 60, 65, 70, 75, 80, and 85, and obtained 91.2% recall. When we increased the number of nodes in the hidden layer to 30, recall improved to 94.8%. But in increasing the number of elevation angles to six (0o, 7o, 15o, 22o, 30o, and 45o), we obtained only 85.4% recall because the neural network was unable to converge during training with the extra data.
Figure 9 shows typical classification errors with respect to azimuth for the best parameters, and Figure 10 shows errors with respect to elevation. “Error” means that an incorrect classification was highest-output class for the neural network over all test examples at that azimuth (Figure 9) or elevation (Figure 10). It can be seen that the errors are abrupt as a function of azimuth, but smoothly varying with respect to elevation.
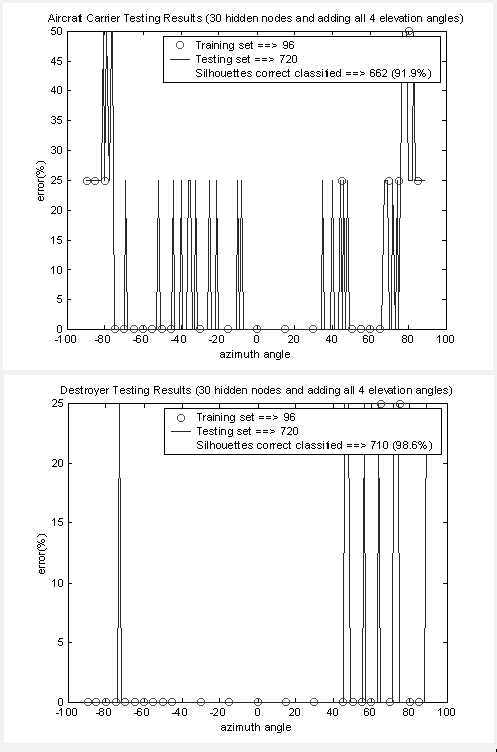
Figure 9: Accuracy with respect to azimuth for aircraft carrier and destroyer
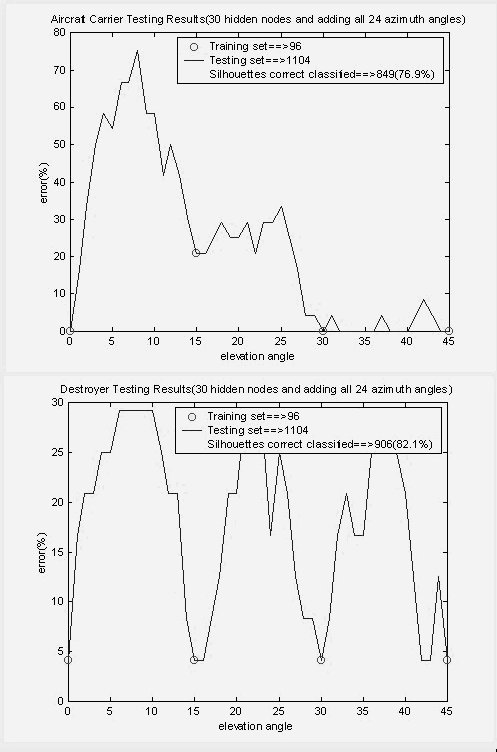
Figure 10: Accuracy with respect to elevation for aircraft carrier and
destroyer
After these initial experiments, we tested the best network on a larger set of model projections taken at 1o increments in azimuth and elevation, totaling 41400 images (180 x 46 x 5). The average recall and precision were 87.3%. Table 1 shows the confusion matrix of counts. Here “Overall Recall” refers to accuracy within the row and “Overall Precision” refers to accuracy within the column. As extra confirmation, we also ran the system on the 25 real infrared images and got an average recall of 68% and precision of 72%. We saw no evidence of overtraining at this size of a training corpus, but did see it when angle increments were further decreased.
|
|
Aircraft Carrier |
Destroyer |
Frigate |
Point Sur |
Merchant |
Overall Recall |
|
Aircraft Carrier |
6711 |
201 |
425 |
393 |
550 |
81.1% |
|
Destroyer |
318 |
7301 |
397 |
257 |
7 |
88.2% |
|
Frigate |
345 |
788 |
6809 |
217 |
121 |
82.2% |
|
Pointsur |
67 |
146 |
177 |
7873 |
17 |
95.1% |
|
Merchant |
297 |
188 |
291 |
49 |
7455 |
90.0% |
|
Overall Precision |
86.7% |
84.7% |
84.1% |
89.6% |
91.5% |
|
Table 1: Confusion matrix for tests of 41,400 silhouettes of ship models.
Computation time averaged one minute per real infrared image, almost all of it during image processing, and this could be much improved by using C++ or Java packages rather than Matlab. Thus there appears little advantage to processing time in attempting to reduce the number of features considered, as by principal-components analysis; ships move slowly and are not usually numerous in any one location, so that classification time is not too critical anyway.
Since performance was not much worse on the real images despite the presence of noise, this suggests training on real images to eliminate the work of constructing detailed geometric models. We need to examine performance for larger numbers of ship types or even individual ships. We also need to eliminate common artifacts like ship shadows, reflections on the sea surface, and heat from stacks that our preprocessing merged into the ship region.
Clearly performance of the neural network approach was much better than that of the edge-histogram approach, and the techniques used are more robust. However, clearly some local feature analysis would help performance judging by the mistakes made, and some of the edge-histogram analysis could provide this. We are currently integrating work into a full ship-identification system that uses electronic emissions, tracking data, and ship-information databases (Lisowski, 2000) to improve classification performance further.
Alippi, C., 1995. Real-time analysis of ships in radar images with neural networks. Pattern Recognition, 28, 12 (December), 1899-1913.
Alves, J., 2001. Recognition of ship types from an infrared image using moment invariants and neural networks. M.S. thesis, U.S. Naval Postgraduate School, March.
Bizer, M., 1989. A picture-descriptor extraction program using ship silhouettes. M.S. thesis, U.S. Naval Postgraduate School, June.
Casasent, D., J. Pauly, and D. Fetterly, 1981. IR ships classification using a new moment pattern recognition concept. In: P. Naendra, Infrared Technology for Target Detection and Classification, SPIE Proceedings vol. 302, 126-133.
C. Chau and W. Siu, 1999. Generalized dual-point Hough transform for object recognition, Proceedings, 1999 International Conference on Image Processing, vol. 1, pp. 560-564.
Dudani, S., K. Breeding, and R. McGhee, 1977. Aircraft identification by moment invariants. IEEE Trans. on Computers, 26, No.1, 39-46.
Freeman, H., 1978. Shape description via the use of critical points. Pattern Recognition 10, pp. 159-166.
Gibbins, D., D. Gray, and D. Dempsey, 1999. Classifying ships using low resolution maritime radar. Proc. of the Fifth International Symposium on Signal Processing and Applications, Brisbane Australia, 325-328.
Gouaillier, V., and L. Gagnon, 1997. Ship silhouette recognition using principal components analysis. In: Applications of Digital Image Processing XX, SPIE Proceedings vol. 3164, 59-69.
Herman, J., 2000. Target identification algorithm for the AN/AAS-44V Forward-Looking Infrared (FLIR). M.S. thesis, U.S. Naval Postgraduate School, June.
Hu, M. K., 1962. Visual pattern recognition by moment invariants. IRE Transactions on Information Theory, 8, 179-187.
Jaggi, S., C. Karl, S. Mallat, and A. Willsky, 1999. Silhouette recognition using high-resolution pursuit. Pattern Recognition 32, 753-771.
Jane’s All the World’s Fighting Ships 1985-1986, 1986. Jane’s Publishing Inc., pp. 216-217.
Kashyap, R., and R. Chellapa, 1981. Stochastic models for closed boundary analysis: representation and reconstruction. IEEE Trans. on Inf. Theory, 27, 109-119.
Lesage, F., and L. Gagnon, 2000. Experimenting level set-based snakes for contour segmentation in radar imagery. Proceedings of SPIE, Volume 4041, Visual Information Processing IX, Orlando, FL, 154-162.
Lisowski, M., 2000. Development of a target recognition system using formal and semiformal methods. M.S. thesis, Naval Postgraduate School, www.cs.nps.navy.mil/people/faculty /rowe/lisowskithesis.htm.
McLenaghan, I. and A. Moore, 1988. A ship infrared signature model. Proceedings of SPIE, Volume 916, Conference on Infrared Systems -- Design and Testing, London, UK, 160-164.
Musman, S., D. Kerr, and C. Bachmann, 1996. Techniques for the automatic recognition of ISAR ship images. IEEE Transactions on Aerospace and Electronic Systems, 32, 4, 1392-1404.
Ornes, C., and J. Sklansky, 1997. A neural network that visualizes what it classifies. Pattern Recognition Letters, 18, 11-13 (November), 1301-1306.
Perantonis, S., and J. Lisboa, 1992. Translation, rotation, and scale invariant pattern recognition by high-order neural network and moment classifiers. IEEE Trans. on Neural Networks, 3, 2, 241-251.
Reeves, A., R. Prokop, S. Andrews, and F. Kuhl, 1988. Three-dimensional shape analysis using moments and Fourier descriptors. IEEE Trans. on PAMI, 10, 6, 937-943.
Richard, C., and H. Hemani, 1974. Identification of three-dimensional objects using Fourier descriptors of the boundary curve. IEEE Transactions on Systems, Man, and Cybernetics, SMC-4, 4, 371-378.
Rogers, S., D. Ruck, M. Kabrisky, and G. Tarr, 1990. Artificial neural networks for automatic target recognition. In: Applications of Artificial Neural Networks, SPIE Vol. 1294, 1-12.
Rowe, N. C., and Grewe, L., 2001. Change detection for linear features in aerial photographs using edge-finding. IEEE Transactions on Geoscience and Remote Sensing, Vol. 39, No. 7, July, 1608-1612.
Teh, C., and R. Chin, 1988. On image analysis by the method of moments. IEEE Trans. on PAMI, 10, 291-310.
Valin, P., Y. Tessier, and A. Jouan, 1999. Hierarchical ship classifier for airborne Synthetic Aperture Radar (SAR) images. Asilomar Conference on Signals, Systems, and Computers, volume 2, 1230-1234.
Withagen, P., K. Schutte, A. Vossepoel, and M. Breuers, 1999. Automatic classification of ships from infrared (FLIR) images. Proceedings of SPIE, Volume 3720, Conference on Signal Processing, Sensor Fusion, and Target Recognition VIII, Orlando, FL, April.
Yuan, C., and Casasent, D., 2002. Composite filters for inverse synthetic aperture radar classification of small ships. Optical Engineering, 41, 1 (January), 94-104.
Acknowledgement: This work was supported by the Naval Postgraduate School under funds provided by the Chief of Naval Research.