Roads, Rivers, and Obstacles: Optimal Two-Dimensional Path Planning around Linear Features for a Mobile Agent
Neil C. Rowe*
Code CS/Rp, Department of Computer Science
U.S. Naval Postgraduate School, Monterey, CA 93943
Abstract
We present an
efficient algorithm for finding least-cost paths for an agent of negligible
size across an important special case of two-dimensional terrain, terrain
consisting of (1) a single isotropic homogeneous-cost-per-distance background
region, (2) "roads" or narrow transportation corridors of low
cost-per-distance, (3) "rivers" or narrow features of high crossing
cost, and (4) untraversable "obstacles". This work extends (Mitchell
1987) by including rivers and new pruning heuristics for roads; our algorithm
remains
in time complexity. We also show results of a first computer implementation for
this class of algorithms, and analyze average-case performance and error
sensitivity. This work applies primarily to high-level path planning for
robots, but also can help plan military maneuvers and guide construction of
roads and pipelines.
* This work was supported in part by the U. S. Army Combat Developments Experimentation Center under MIPR ATEC 88-86. The views and conclusions contained in this document are those of the author and should not be interpreted as representative of the official policies of the Army or the U.S. Government. Thanks to Robert Richbourg and Robert McGhee. This paper appeared in International Journal of Robotics Research, 9, no. 6 (December 1990), pp. 67-74. Equations were redrawn in 2008.
Introduction
We address finding the best path for an agent of negligible size across a known two-dimensional area or terrain, if the path can go anywhere except "obstacle" regions. "Best" can mean minimizing cost, effort, time, the probability of accident, or anything else proportional to distance traversed within homogeneous terrain. The general problem requires the calculus of variations, but when isotropic terrain is homogeneous except for obstacles (Lozano-Perez and Wesley 1979) or consists of polygonal homogeneous-cost regions (Richbourg et al 1987; Rowe and Richbourg 1990; Mitchell 1988), the problem can be provably reduced to a graph search over a finite graph. "Roads" (Mitchell 1987; Gewali et al 1988), low-cost corridors of negligible width, represent a special case of the latter subproblem in which special efficient algorithms can be devised. But no implementations for the latter case have yet been done.
The work mentioned, and the algorithm of this paper, reason from intrinsic terrain geometry. An alternative is reasoning from a terrain grid as in dynamic-programming "wavefront propagation" methods (Chavez and Meystel 1984; Mitchell and Keirsey 1984) that then search the grid as a graph. While wavefront-propagation algorithms are preferable in many applications, they have several disadvantages (discussed further in (Rowe and Richbourg 1990)) that suggest exploring other algorithms. First, the grid is not likely to correspond to natural terrain features, causing approximation errors which can accumulate. Second, the best grid size may vary considerably over the terrain, and is hard to choose. Third, the algorithms consistently overvalue travel in certain directions; more complex propagation formulae which decrease this bias also reduce resolution. Fourth, the approach is computationally wasteful, as it explores blindly in every possible direction. Thus, we have not used wavefront-propagation methods in our work.
Local criteria for optimal paths at roads, rivers, and obstacles
Finding optimal paths across terrain modeled by isotropic homogeneous-cost-per-distance polygonal regions (the "weighted region problem") necessarily requires considerable analysis once a start and goal point are selected. But we show in this paper that when otherwise-uniform terrain contains three special cases of weighted regions--"roads", "rivers", and "obstacles"--considerably more simple preanalysis of the terrain can be done, greatly simplifying subsequent searches. Roads are the limiting case of a low-cost region as its width decreases to zero while its cost-per-distance is held constant; rivers are the limiting case as the width decreases and the cost to cross remains constant (i.e., an impulse function); obstacles are the limiting case as cost increases and dimensions are held constant. The three cases cover many important overland terrain phenomena including highways, paths, transportation lines, power lines, walls and fences, and boundaries of areas of impenetrable vegetation or unsafe surface.
Our approach is to exploit local optimality criteria that optimal paths must follow on such special terrain features. Our basic principle we call the Shortcut Meta-Heuristic, and is the discrete-mathematics analog of the basic principle of the calculus of variations: At any turn on an optimal path from some start point to some goal point, any shortcut across that turn must be impossible or undesirable compared to the optimal-path detour. An immediate corollary is that optimal paths must run straight in the interiors of homogeneous regions because cost accrued there depends only on distance, and a straight line is the shortest distance between two points. We show now that the Shortcut Meta-Heuristic applied to piecewise-linear roads, rivers, and obstacle boundaries says that their vertices are nearly the only places where turns can occur on optimal paths. (We ignore the problem of obtaining piecewise-linear models of terrain features in this paper, as this is a well-studied problem in computational geometry.)
Specifically, let offroad "background" terrain have a cost per
unit distance 
;
let roads have a cost per unit distance 
; and let the cost of crossing a river
segment be a fixed constant k. (Section 7 generalizes the algorithm to terrain
of variable-such parameters.) We prove three important heuristics for optimal
paths on roads. We first prove Road Heuristic 1: any turn offroad to onroad or
vice versa on an optimal path cannot turn more than the critical angle 
. Consider a path
segment of length L from off a road to a road, a segment that is followed by a
turn of angle θ onto the road. If it would be worse to instead go directly
to a point some infinitesimal amount ε further down the road, from the
same offroad point, 
. Since ε is small, we can ignore
the 
term
under the square root, then take the first two terms of the binomial series for
the square root, obtaining 
, and hence 
.
We next prove Road Heuristic 2: any onroad-offroad transition on an optimal
path cannot form an angle less than C with any road segment (not necessarily
the one followed by the path) with an endpoint at the point of transition. Now
if the path is truly optimal, it must cost less than shortcutting to some point
ε closer on that road segment, and then proceeding from there to the
original transition point. The mathematics is the same as above except that ε
is subtracted rather than added, giving 
, and hence 
.
We finally prove Road Heuristic 3: any turn from one road segment to another
road segment on an optimal path cannot be more than 2C, C the critical angle.
Consider a shortcut across a road turn that creates an isosceles triangle with
the turn vertex. Let θ be the angle of the road turn (so 180-θ is the
angle at the vertex of the triangle), and let x be the distance of the turn
vertex from either shortcut endpoint. Then the shortcut cost does not improve
on the two-part road path between its endpoints if 
, which implies 
after
simplification.
These three heuristics have four immediate important corollaries. Heuristics 1 and 2 imply that any optimal-path onroad-offroad transition at the middle of a straight road segment must involve a turn of exactly C (Corollary 1, also proved in (Mitchell 1987)). Heuristics 1 and 2 imply that no onroad-offroad transition can occur at the inside of a road bend (two-segment road vertex), since any entry angle that satisfies Heuristic 1 would need to violate Heuristic 2 and vice versa (Corollary 2). Heuristic 1 implies that any offroad-onroad transition at a road "dead end" (a road vertex with only one associated road segment) must involve a turn of less than C (Corollary 3, also proved in (Mitchell 1987)). Finally, Heuristic 2 implies that no optimal path can make an offroad-onroad transition at a road vertex at which all road segments make an angle less than 2C with at least one other segment (Corollary 4).
Now let us turn to rivers and obstacles. With piecewise-linear modeling of them, the Shortcut Meta-Heuristic implies that the optimal path between any two points (not necessarily river or obstacle points) can only turn on rivers and obstacles at their vertices. This is since away from roads in order to be undesirable or impossible, any shortcut across a turn on the optimal path must be guaranteed to cross either an obstacle or a river segment not crossed by the detour on the optimal path. So the turn point P must be infinitesimally close and hence equivalent to an obstacle or river vertex, because the obstacle or river that crosses the shortcut must turn or end to avoid crossing the optimal path.
Furthermore, if P is an obstacle vertex, the turn must enclose the obstacle in its bend (so any shortcut would be sure to cross it), which we will call the Obstacle Heuristic. And if P is a river vertex, the turn must enclose more of the river segments meeting at P than it does not enclose, which we will call the River Heuristic. (Enclosure can include coincidence with river segments.) So at a river endpoint (as at a "bridge"), an optimal-path turn must enclose the endpoint; at a bend in a river, a turn must enclose the vertex and both edges; and at a junction of three or more river edges, a turn must enclose the majority of them. (Let optimal paths always pass slightly to one side of a vertex, so we avoid the issue of how many segments are crossed going right through the vertex.) So for the particularly common case of river-bend vertices, the only headings an optimal path turning there can have are headings between and including those of the two river segments.
It would seem that when following along a river, we would need to keep track of which bank of the river we were on, because we would cross different "tributaries" when following each. But surprisingly, it does not matter to total path cost. The Shortcut Meta-Heuristic requires that anytime an optimal path makes a right turn at a river vertex it must pass clockwise around the vertex, and counterclockwise for a left turn. So to avoid unnecessary crossings, the number of rivers crossed at any turn of the optimal path at a river vertex must be the number of river segments touching at that vertex and lying strictly outside the angle of the turn--except where a clockwise turn to follow a river segment is immediately followed by a counterclockwise turn, or vice versa, because then is it necessary to cross the river segment followed between. (Note the crossing place does not matter to the cost.) So the number of rivers crossed at a river vertex is the number of river segments incident at that vertex but strictly to the outside of the turn at the vertex, plus a "correction factor" of k if the river vertex was reached by following along a river segment and the previous path turn was in the opposite sense (clockwise versus counterclockwise) of the turn at this vertex.
A roads-rivers-obstacles algorithm
The results of the previous section require that optimal paths over isotropic homogeneous terrain with embedded piecewise-linear roads, rivers, and obstacle boundaries must be themselves piecewise-linear, turning only at road, river, or obstacle vertices, or onto roads at the critical angle determined by the ratio of road and offroad costs. These restrictions mean we can apply a two-phase algorithm to do optimal-path planning on such terrain, the first phase preprocessing the terrain map, and the second phase finding the path between given start and goal points.
Phase 1 Step 1: Model all roads, rivers, and obstacle boundaries by line segments.
Phase 1 Step 2: Augment this graph by all valid optimal "shortcuts" between these features by iterating over all feature vertices, and using the local optimality criteria of section 2. This is the most complicated step; see the discussion below.
Phase 1 Step 3: Prune further the set of candidate road shortcuts by removing all which form an angle less than the critical angle
Phase 2 Step 1 (to be done once start and goal points are given): Augment the graph made in phase 1 with start and goal points, and construct optimal shortcuts between them and all road segments, road vertices, river vertices, and obstacle vertices, using the standard pruning criteria.
Phase 2 Step 2: Remove from the graph all those edges and edge portions that lie outside the ellipse whose foci are the start and goal points, whose major axis is the distance between the foci F times the ratio (call it R) of the average cost of the shortest path between the foci to the road cost per distance
. (The shortest path is a straight line unless it intersects obstacles, in which case we must do a search like (Lozano-Perez and Wesley 1979.)) The ellipse represents how far the optimal path could travel from the start and goal points at cost rate
Phase 2 Step 3: Now the problem has been reduced to weighted graph search. Use the A* algorithm. The cost lower bound is the distance to the goal times
In all these steps, if mixtures of roads, rivers, and obstacles meet at a vertex, treat the vertex as two or three coincident nonmixture vertices. For efficiency we can combine phase 2 steps 1 and 2, but not phase 1 steps 2 and 3 because later shortcuts can allow pruning of earlier shortcuts. (Mitchell 1987) provides an additional heuristic we could exploit, concerning crossing roads at shallow angles. Bidirectional A* search (de Champeaux and Sint 1977) could help in the phase 2 step 3 since problem is reversible. If still more speed in required in phase 2, we can prune in phase 1 step 3 each candidate shortcut for which a shorter path between its endpoints exists; an A* search can determine this, but this can be computationally expensive to do for every shortcut.
Details of phase 1 step 2
Phase 1 step 2 requires an inner and outer loop. In the outer loop we consider in turn each road, river and obstacle vertex V. Then in an inner loop for V a river or obstacle vertex, we consider in turn each road edge, river vertex, and obstacle vertex to which vertex V might connect directly in an optimal path; in an inner loop for V a road vertex, we consider each road segment as a start of a shortcut to V. Whenever a proposed shortcut is found in either inner loop, it must be confirmed not to intersect an obstacle.
In the rivers-obstacles inner loop, we can eliminate possibilities with the River Heuristic and the Obstacle Heuristic. This means that there can be no shortcuts to the inside of river bends. It also means that no shortcut to the outside of a river bend can occur if a straight-line continuation of the shortcut crosses the river there, and no shortcut to an obstacle vertex can occur if a straight-line continuation of the shortcut enters the obstacle. These are strong restrictions.
Handling of road vertices is more complex. For a non-road vertex V and a
road segment E, let the range of headings from V to E be 
. Then if 
is one of the
headings of E and C is the critical angle, there is a shortcut at heading 
if it is
between 
and
, and at
heading 
if
thtat is between them. There is also a shortcut to endpoint vertex W of E at
heading if
another road segment incident on W has heading 
and either 
or 
is between and (taking in the
direction consistent with , i.e. if approaches W along E
then leaves
W along W1). For a road vertex V and a road segment E, additional constraints
must be imposed at V. First, obtain the candidate shortcuts valid according to
the preceding mathematics. Then for each shortcut endpoint on E, apply the
criteria of the last paragraph in reverse, from the shortcut end on E to V, to
further rule out candidates.
An implementation
We implemented all except phase 2 step 2 of the above algorithm in Edinburgh C-Prolog (for simplicity, we picked test cases where all the data would fall into a phase 2 step 2 ellipse). Figure 1 shows an example of performance in planning between a point in the lower left and a point in the upper right. The offroad cost was 1.4 per inch, the onroad cost was 1 per inch, and the river-crossing cost was 0.2, where in the original scaling the terrain map was about 7 inches high.
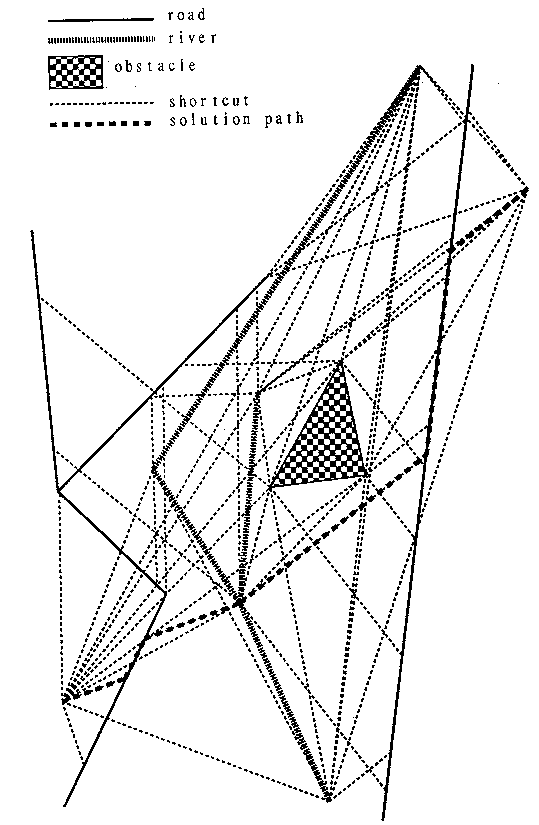
Figure 1
Figure 2 shows the results of more extensive test runs on the same terrain. Here the road cost was 2, the offroad cost 1, and the river-crossing cost 1.5. The goal point was on the right side toward the bottom. 1656 (=36x46) evenly-spaced start points were tested. Figure 2 shows the initial direction of the optimal path for each, providing a picture of the optimal-path field for this terrain and goal. Superficially the picture resembles the back-pointer array created by wavefront-propagation path-planning methods, but note the subtle phenomena recorded by permitting an infinity of possible vector directions instead of the typical eight directions of wavefront propagation. Note also that initial path directions only change abruptly in vicinity of strongly competing influences. Such optimal-path fields are investigated further in (Alexander 1989).
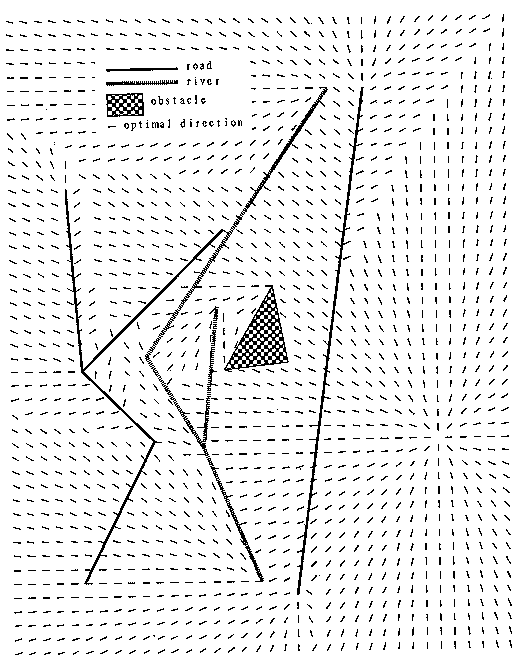
Figure 2
Execution time of the algorithm
(Mitchell, 1987) gives the time complexity of his algorithm for terrain with
roads and obstacles of where n is the number of road
and obstacle vertices, for an algorithm including phase 1 step 2, phase 2 step
1, and phase 2 step 3. Our algorithm does the same visibility-graph
construction and similar examination of river vertices as he does with road
vertices, and all our pruning criteria use the same information (edges incident
at a vertex) that he does, so our algorithm is also . But this result is not
very informative, so we give here an average-case analysis of our algorithm.
The average running time of phase 1 step 1 will be highly terrain-dependent.
But the key step 2 of phase 1 is more analyzable. Suppose the result of phase 1
step 1 is E road segments, 
road vertices, 
river
vertices, and 
obstacle
vertices. Then the inner loop is executed 
times. Each pass requires some
fixed heading checks, plus lookups to find the road and river segments adjacent
at vertices. The lookups can be indexed in advance, then done with
approximately 
operations
for roads, 
for
rivers. So the time for phase 1 step 2, not counting obstacle-intersection
checking, will be proportional to 
.
The number of shortcuts created in phase 1 step 2 can be estimated by a few
reasonable assumptions. Suppose the great majority of road and river vertices
are two-segment bends, as is common in modeling real-world roads and rivers.
Suppose at a typical bend the road, river, or obstacle boundary turns A
degrees. A randomly chosen shortcut heading for a river or obstacle vertex will
have a chance of 2A/360 of being permissible there (since it must lie outside
the bend, and permit enclosure of the bend by the optimal path). A randomly
chosen shortcut heading for a road vertex will have a similar probability of
permissibility at that end of the shortcut (for ranges of headings of departure
for a shortcut, for the two directions of travel through the turn). A randomly
chosen shortcut heading for a road edge will have a success probability
proportional to the average angular width, call it W, of a random edge from a
random vertex. So the expected number of shortcuts created in phase 1 step is 
, considerably
better for small A than the worst case of .
Now we can complete our analysis of phase 1 step 2: The S shortcuts found
will require 
calls
to an intersection routine to check whether they intersect obstacles, with the
simplest possible approach. The phase 1 step 3 pruning criteria require
negligible effort since they affect only to the rare road junctions at which
other than two road segments meet. Both steps 1 and 2 of the phase 2 of the
algorithm require iterating over all the vertices to do some simple checks, for
operations.
Step 1 will add approximately 
new shortcuts. Step 2 will
delete a highly terrain-dependent and problem-dependent number, leaving a
number we will call T. Then step 3 is an A* search over the remaining T edges,
requiring effort proportional to T log T.
Cost error analysis
Execution time trades off with resolution of the piecewise-linear modeling.
We can assume that during linearization of terrain features, terrain topology
is maintained, model road and river vertices are always placed in the middle of
road and river locations, obstacle-boundary vertices always placed on
obstacles, and junction vertices always placed at the middle of junctions.
Nonetheless, the linearization of terrain features causes road, river, and
obstacle-boundary segments to be lengthened or shortened compared to the real
world, changing estimated path costs. Suppose our algorithm finds an n-segment
"optimal" path; for each path segment i following a road, river, or
obstacle-boundary segment, we can define (1) 
, the maximum deviation
(nonnegative) of the segment from the real-world feature between its endpoints,
and (2) 
,
the excess length of the real-world feature between its endpoints. Many phase 1
step 1 algorithms upper-bound both for the entire map. We can take the cost
error of all other path segments to be zero (it does not matter where you cross
a road, and we can assume path-followers are smart enough to take the better
side of river and obstacle vertices). Again let be the background cost rate, the onroad
cost rate, and C the critical angle.
Wherever the path found by the algorithm goes from road to offroad or vice
versa, the real-world location of the road might be displaced a maximum of to the far
side. And the excess length of the real-world road might be all
concentrated in the part of the road segment used by the path. With a river or
obstacle boundary, there can only be an error of the second (feature-following)
type, but then there is an "detour" alternative path: we could start
at one endpoint of the segment, move perpendicular to it, travel
parallel to the segment, and then reach the other endpoint by returning
distance perpendicularly
to the segment; by the definition of , this is guaranteed not to cross a
river or actual obstacle boundary provided no other rivers or obstacles are
within distance of
the model segment. Simlar detours may be necessary when the optimal path merely
touches a vertex of a highly curving river or obstacle boundary. In summary,
the maximum underestimate in the cost of the optimal path that can be made by
our algorithm is just the sum for all path segments of either (1) 
, for segment i a
road segment followed up to a road endpoint; (2) 
for segment i a road segment
used only partially, then followed by an offroad segment not departing from an
endpoint; (3) 
for
segment i an offroad segment shortcutting to the interior of a road segment;
(4) 
for
segment i a river or obstacle-boundary segment; (5) 
for segment i touching
a river or obstacle vertex but not following a river or obstacle segment, where
j ranges over the river or obstacle segments at that vertex; or (6) 0
otherwise.
Wherever the actual road reaches an extreme on the near side of the
straight-line model road segment, then the offroad distance saved could be at
most 
(when
the true optimal path turns onto a true road when it gets within of the model
road segment); and no distance can be saved over a straight line along the
model road segment. Following or touching of river and obstacle-boundary
segments cannot cost less than the algorithm-computed cost. So the maximum
overestimate in the cost of the optimal path that can be made by our algorithm
is the summation for all path segments of either (1) 
, for segment i a road
segment used only partially and adjacent to an offroad segment not departing
from an endpoint; (2) 
, for segment i an offroad segment
shortcutting to the interior of a road segment; (3) or otherwise 0.
Extension to variable-cost roads and rivers
It is straightforward to extend our algorithm to road segments of differing
costs 
.
Now the critical angle depends on the segment. In the mathematics of section
3.1, at a road vertex now where segment E has cost 
and segment W1 has
cost 
,
there is a shortcut to the vertex if either is between 
and 
or is between 
and 
. If river
segments have different crossing costs 
, then the Shortcut Meta-Heuristic
requires that an optimal-path turn enclose segments incident on the turn vertex
whose sum of is
greater than that of those incident but not enclosed. Modified corollaries
follow from these modified heuristics.
References
Alexander, R. 1989 (September). Construction of optimal-path maps for homogeneous-cost-region path-planning problems. Ph.D. Thesis, U.S. Naval Postgraduate School, Department of Computer Science.
de Champeaux, B., and Sint, L. 1977. An improved bi-directional heuristic search algorithm. Journal of the ACM 24: 1777-1791.
Chavez, R. and Meystel, A. 1984 (Atlanta, Ga.). Structure of intelligence for an autonomous vehicle. IEEE International Conference on Robotics and Automation. New York: IEEE, pp. 584-591.
Gewali, L., Meng, A., Mitchell, J., and Ntafos, S. 1988 (June, Urbana Ill.). Path planning in 0/1/infinity weighted regions with applications. Proceedings of the Fourth Annual ACM Symposium on Computational Geometry. New York: ACM, pp. 266-278.
Lozano-Perez, T. and Wesley, M. A. 1979 (October). An algorithm for planning collision-free paths among polyhedral obstacles. Communications of the ACM 22(10): 560-570.
Mitchell, J. S. B. and Keirsey, D. 1984. Planning strategic paths through variable-terrain data. SPIE Conference on Applications of Artificial Intelligence. New York: SPIE, volume 485, pp. 172-179.
Mitchell, J. S. B. 1987 (May). Shortest paths among obstacles, zero-cost regions, and roads. Paper delivered at the Joint National Meeting of TIMS/ORSA, New Orleans, La.
Mitchell, J. S. B. 1988. An algorithmic approach to some problems in terrain navigation. Artificial Intelligence 37: 171-201.
Richbourg, R., Rowe, N., Zyda, M., and McGhee, R. 1987 (March, Raleigh, North Carolina). Solving global two-dimensional routing problems using Snell's Law and A* search. Proceedings of the IEEE International Conference on Robotics and Automation. New York: IEEE, pp. 1631-1636.
Rowe, N. C. and Richbourg, R. F. 1990. An efficient Snell's-law method for optimal-path planning across multiple two-dimensional irregular homogeneous-cost regions. To appear in International Journal of Robotics Research. Also Technical Report NPS52-88-017, Monterey, Calif.: U. S. Naval Postgraduate School, Department of Computer Science.