Load Balancing of Parallelized Information Filters
Neil C. Rowe and Amr Zaky\
Code CS/Rp, Department of Computer Science
Naval Postgraduate School
Monterey, CA USA 93943
rowe@cs.nps.navy.mil
Abstract
We investigate data-parallel implementation of a set of "informationfilters" used to rule out uninteresting data from a database or datastream. We develop an analytic model for the costs and advantages ofload rebalancing of the parallel filtering processes, as well as a quick heuristic for its desirability. Our model uses binomial models of the filter processes, and fits key parameters to results of extensive simulations. Experiments confirm our model. Rebalancing should pay off whenever processor communications costs are high. Further experiments showed it can also pay off even with low communications costs for 16-64 processes and 1-10 data items per processor; then imbalances can increase processing time by up to 52% in representative cases, and rebalancing can increase it by 78%, so our quick predictive model can be valuable. Results also show our proposed heuristic rebalancing criterion gives close to optimal balancing. We also extend our model to handle variations in filter processing time per data item.
Index terms: information filtering, data parallelism, load balancing, information retrieval, conjunctions, optimality, and Monte Carlo methods.
This paper appeared in IEEE Transactions on Knowledge and Data Engineering, vol. 14, no. 2 (March/April 2002), 456-461.
Suppose we have a query which is a conjunction of restrictions on data we wish to retrieve from a big database. These restrictions can be considered as "information filters" [1], or as programs that take some set of data items as input and return some small subset of "interesting" items as output. For instance, in retrieving pictures of buildings under construction, we can look in an index first for the pictures that show buildings and then exclude those that do not show construction, applying two information filters in succession. Signature methods [4] are an important subcase of information filtering; these check against hashes of information in a complex data structure. We would like to filter in the fastest way. [8] and [5] discuss the potentially dramatic advantages of reordering the conjuncts and of inserting redundant conjuncts. But those results are primarily for sequential machines.
Efficiency issues are becoming increasingly important with multimedia libraries [9]. Multimedia data can be considerably more costly to retrieve than text data; for instance, a long paper requires 10K bytes while a single television picture requires 1000K, so data transfer is slower and slower storage media are often required. Content analysis of multimedia data can be very slow; recognizing a shape in a picture, for instance, requires complex data structures and many passes through the picture. So it helps considerably to summarize multimedia data and index it. Information filters can then check the indexes quickly. Parallel information filtering then could speed things considerably more. For instance, to find pictures of buildings under construction when we have 100 processors, we could have each of the 100 look in a different part of the database, or alternatively we could have 50 look for buildings in the database while 50 looked for things under construction.
While optimization of parallel information filtering is a scheduling problem, general scheduling methods such as [11] are too general to be efficient for it. Also not directly helpful are experiments with expensive massively-parallel machines [10] and with thousands of filters [7], since the resources required for those approaches are beyond the capabilities of most computer facilities and workstations, precluding real-time application of the methods there. Instead, we will assume under 100 filters and easily available multiprocessor software, and we will exploit the problem-specific feature that each filter in a filtering sequence has fewer data items to work on.
Section 2 of this paper proves by a theorem that we can narrow our investigation to data parallelism. Section 3 introduces the statistical metrics we will need to assess the benefits and costs of load balancing, and will develop quick approximations of them. Section 4 discusses the obvious cases for load balancing in data-parallel filtering, and then develops a simple and quick criterion for when it is desirable. Section 5 extends these results into an algorithm for deciding where to balance loads in a long sequence of filters. Section 6 reports on a wide range of simulation experiments we conducted; Section 7 reports more focused experiments about an IRIS multiprocessor. All experiments supported our analytic models. Section 8 extends the results of Sections 3 and 4 to the case in which filter cost per data item can vary.
2. Assumptions
Suppose data items must pass through m information filters; that is, a data item must separately pass the test administered by each filter if that data item is to be part of the query answer. Assume the event of a data item passing a test is independent of the event of any other data item passing any test. Assume each filter has an average cost of execution per data item of ![]() and an a priori probability of passing a random data item of
and an a priori probability of passing a random data item of ![]() where
where ![]() to avoid considering trivial cases. Let
to avoid considering trivial cases. Let ![]() be the probability of passing filters i through j. Assume further that times are independent of probabilities, or that the time to test whether an item passes a filter is independent of the success or failure of the test or any other test on that data item; this is true of testing of uniform-size data by hash table lookups in signature files, for instance. If the filters are applied in sequence, the expected total time per data item of passing filters 1 through m will be:
be the probability of passing filters i through j. Assume further that times are independent of probabilities, or that the time to test whether an item passes a filter is independent of the success or failure of the test or any other test on that data item; this is true of testing of uniform-size data by hash table lookups in signature files, for instance. If the filters are applied in sequence, the expected total time per data item of passing filters 1 through m will be:
![]() The time and probability parameters can be estimated either from past statistics of the filters on similar problems, or by applying the filters to a small random sample of the database.
The time and probability parameters can be estimated either from past statistics of the filters on similar problems, or by applying the filters to a small random sample of the database.
Now suppose we have R identical processors available on a single-user multiprocessor. We can show that it never makes sense to execute different information filters in parallel given the reasonable assumption that initialization time is proportional to the number of processors. That is because data parallelism, where all processors work on the same filter at the same time, is provably better.
Data-Parallelism Theorem: Suppose the execution time of two information filters in parallel (functional parallelism) for a set of data items is ![]() where
where ![]() is a constant, R is the number of available identical processors,
is a constant, R is the number of available identical processors, ![]() is the number of processors allocated to filter i, and
is the number of processors allocated to filter i, and ![]() is the total execution time cost for filter i. Then functional parallelism is always slower than data parallelism for those processors.. Proof: The time for data parallelism (using all R processors for one filter, then all R for the other filter) is
is the total execution time cost for filter i. Then functional parallelism is always slower than data parallelism for those processors.. Proof: The time for data parallelism (using all R processors for one filter, then all R for the other filter) is ![]() if filter 1 goes first, and
if filter 1 goes first, and ![]() if filter 2 goes first, where
if filter 2 goes first, where ![]() is the probability of success of filter i. The time for functional parallelism is
is the probability of success of filter i. The time for functional parallelism is ![]() assuming negligible time to intersect the results of the two filters. The minimum of the latter with respect to
assuming negligible time to intersect the results of the two filters. The minimum of the latter with respect to ![]() occurs with perfect load balancing (if possible) of the two processors, or when
occurs with perfect load balancing (if possible) of the two processors, or when ![]() or when
or when ![]() . Then the time becomes
. Then the time becomes ![]() . Comparing terms with the formula for data parallelism with filter 1 first, we see
. Comparing terms with the formula for data parallelism with filter 1 first, we see ![]() ,
, ![]() , and
, and ![]() . Comparing terms with the formula for data parallelism with filter 2 first,
. Comparing terms with the formula for data parallelism with filter 2 first, ![]() ,
, ![]() , and
, and ![]() . Hence functional parallelism is always slower than data parallelism even with our conservative assumptions and no matter what R,
. Hence functional parallelism is always slower than data parallelism even with our conservative assumptions and no matter what R, ![]() ,
, ![]() , and k are (and even if
, and k are (and even if ![]() ). QED.
). QED.
Thus data parallelism is the best way to exploit R identical processors for filtering. For maximum advantage we should assign data items randomly to processors to prevent related items from ending up on the same processor and affecting its rate of filtering success. We should also initially assign equal numbers of data items to each processor if processing time per data item is either constant or unpredictable. Data items should remain with their processors for the second and subsequent filtering actions if necessary, so no data needs to be transferred between processors, and a processor that finishes early on a filter can start early on the next.
But if the number of remaining data items per processor can vary significantly over processors after a sequence of filtering actions, data transfers might significantly reduce total processing time. General load-balancing algorithms for data-parallel computations (like [6] using run-time decision-theoretic analysis and [3] using run-time monitors of processor performance) could be used, but information filtering is a special case for which special techniques should work better. Filtering is a chain of simple linearly-dependent actions, and we can randomly assign data to processors. This means that associated random variables will fit well to classic distributions like the binomial and normal, unlike many applications of data parallelism.
3. Estimating the degree of load imbalance
We need to model the expected load imbalance after applying filters on multiple identical data-parallel processors, or the degree to which some processors will have more data items to work on than others even when they start with the same number. The event of a random data item passing filters 1 through i is a binomial process. For n data items initially supplied to each processor (for ![]() total data items), the expected mean number of data items resulting from filter i on a processor will be
total data items), the expected mean number of data items resulting from filter i on a processor will be ![]() and the standard deviation about that mean will be
and the standard deviation about that mean will be ![]() . The
. The ![]() decrease monotonically with i, so both the mean and the standard deviation of the expected number of data items remaining will decrease; but generally filter time
decrease monotonically with i, so both the mean and the standard deviation of the expected number of data items remaining will decrease; but generally filter time ![]() increases in a good sequence order [8] (quick filters should generally be first to reduce work faster), so it is not easy to guess the best places to rebalance.
increases in a good sequence order [8] (quick filters should generally be first to reduce work faster), so it is not easy to guess the best places to rebalance.
We assume for now that filtering time is the same for every data item, as with common filtering methods like lookups in hash tables. Thus an extra k data items, for a filter that requires time of ![]() per
per
data item, mean an extra ![]() in processing time. But Section 8 will provide some results when filtering time can vary.
in processing time. But Section 8 will provide some results when filtering time can vary.
Two statistics helpful for analyzing imbalance are the excess number of data items supplied to the most overburdened of R processors (which measures the benefit of rebalancing), and the minimum number of data items that must be transferred among R processors to rebalance them (which measures the cost of rebalancing). Mathematically, these are respectively the difference between the maximum and mean of R random variables drawn on a binomial distribution (what we will call "maxdev"), and the average of the absolute values of the deviations of the same R variables about their mean (what we will call "absdev") times R. "Maxdev" is usually the ![]() norm used in numerical analysis [2] (since our distributions usually skew towards the maximum) and "absdev" is the
norm used in numerical analysis [2] (since our distributions usually skew towards the maximum) and "absdev" is the ![]() norm. Published analysis of these norms usually assumes a normal distribution, not a good approximation for a binomial distribution in this application where both the number of data items and the probability of filter success can be very small. So we pragmatically used "Monte Carlo" techniques (experiments with random numbers) and regression on the results of the experiments to get approximate formulas relating "maxdev" and "absdev" to the standard deviation of the binomial distribution, since intuitively both should be proportional to the standard deviation.
norm. Published analysis of these norms usually assumes a normal distribution, not a good approximation for a binomial distribution in this application where both the number of data items and the probability of filter success can be very small. So we pragmatically used "Monte Carlo" techniques (experiments with random numbers) and regression on the results of the experiments to get approximate formulas relating "maxdev" and "absdev" to the standard deviation of the binomial distribution, since intuitively both should be proportional to the standard deviation.
We generated sets of 8192 random variables on binomial distributions with probabilities ![]() for
for ![]() to
to ![]() and with universe sizes
and with universe sizes ![]() for
for ![]() to
to ![]() . We then computed "maxdev" and "absdev" taking those variable values as the number of data items on R processors,
. We then computed "maxdev" and "absdev" taking those variable values as the number of data items on R processors, ![]() for
for ![]() to
to ![]() . Since magnitudes of these parameters vary widely, it makes sense to take their logarithms before doing a regression. The best models found corresponded to the equations:
. Since magnitudes of these parameters vary widely, it makes sense to take their logarithms before doing a regression. The best models found corresponded to the equations:
![]()
![]()
where ![]() is the observed standard deviation of the number of items remaining after filter i has been applied; its theoretical value is
is the observed standard deviation of the number of items remaining after filter i has been applied; its theoretical value is ![]() , where b is number of the most recent previous filter before which the data items were balanced. The coefficient of determination (or degree of confidence) was 0.983 for "maxdev" and 0.981 for "absdev". We investigated the addition of a number of other terms to these models, but none added anything statistically significant. Note the closeness of the exponents of
, where b is number of the most recent previous filter before which the data items were balanced. The coefficient of determination (or degree of confidence) was 0.983 for "maxdev" and 0.981 for "absdev". We investigated the addition of a number of other terms to these models, but none added anything statistically significant. Note the closeness of the exponents of ![]() to 1 which says these statistics are closely connected to the standard deviation.
to 1 which says these statistics are closely connected to the standard deviation.
As an example, suppose we have 8000 data items, 16 identical processors, and a filter with success probability ![]() (probability of a random data item of passing the filter) of 0.1. Then 500 data items should be initially assigned to each processor. An expected number of 50 data items per processor should remain after applying the filter, with a standard deviation over processors in the number of data items remaining of
(probability of a random data item of passing the filter) of 0.1. Then 500 data items should be initially assigned to each processor. An expected number of 50 data items per processor should remain after applying the filter, with a standard deviation over processors in the number of data items remaining of ![]() . Our formulas then say
. Our formulas then say ![]() and
and ![]() . This says that on the average, the most overburdened of the 16 processors after the first filter will have 11.05 more data items than the average processor; and the average processor will need to send or receive 5.719 data items in order to rebalance after the first filter.
. This says that on the average, the most overburdened of the 16 processors after the first filter will have 11.05 more data items than the average processor; and the average processor will need to send or receive 5.719 data items in order to rebalance after the first filter.
4. Evaluating the benefits and costs of load balancing of filter processors
One way to rebalance is incremental: Have a "control" processor or shared memory keep lists of data items that need to be filtered, one for each filter plus a final-result list. When a filter processor becomes idle, it asks the control processor to send it some item from the list for filter i for some i and the control processor deletes the item from the list. The filter processor applies filter i to the item. If the item passes, the processor returns it to the control processor to be added to the list for filter i+1. Initially, all lists are empty except the list for filter 1, which should contain all data items; work terminates when all lists are empty except possibly the final-result list.
This method is simple and prevents any significant imbalance. Unfortunately, it entails considerable message traffic and resource contention for the control processor since each filtering action on each data item requires messages to and from the control processor. This is intolerable in the many important applications where communication is costly, as for filters on different Internet sites or for remote environmental sensors distributed over a terrain. This can also be intolerable with lesser communications costs and a large number of data items or processors, especially if filtering requires much information about the data item as with the multimedia data items that are our chief application interest. A fix might be to store on each filtering processor all the information about every data item, so that only item pointers need be transferred to and from the control processor. But that could entail impossible memory requirements in each processor, as for millions of multimedia data items.
In general, some load balancing will usually be desirable whenever communications costs between filters are large and some filters are costly. That does not mean, however, balancing before every filter. The imbalance may not be large enough, nor the expected cost improvement. And judicious balancing can still be desirable even with low communications costs. So we need to analyze a sequence of filters carefully to find good balancing opportunities.
We explore the following efficient rebalancing method using some ideas from Section 6.2 of [11]. Assume that each process when completing filter i reports its number of data items remaining to a control processor. (Centralized control is more efficient than rebalancing by messages between pairs of processors since obtaining perfect balance requires information from all processors.) When the control processor receives messages from all R processors for filter i, and if the difference between the number of data items on the busiest and least-busy processors is large enough, it sends orders to the processors to transfer certain numbers of data items. These transfers need not slow processing much if processors have already begun filter i+1 because the transferred items can be done last when executing filter i+1.
Perfect balance is impossible when the number of data items is not a multiple of R. But if each processor timestamps information sent to the central processor, compensation can be done later by giving earlier finishing processors additional items to work on. For instance with three processors and 28 data items, one processor must initially take 10 items instead of 9. Suppose the next filter passes 6 of the 10, 4 of the 9, and 4 of the other 9. If each filter takes the same amount of time per data item, transfer one of the 6 to each of the other two processors, and this should compensate.
Now let ![]() be the time for a processor to report its set size; let
be the time for a processor to report its set size; let ![]() be the time for a processor to receive, decipher, and initialize a rebalancing order from the control processor; let
be the time for a processor to receive, decipher, and initialize a rebalancing order from the control processor; let ![]() be the time per data item for a processor to transmit or receive a single data item to or from another processor; and let
be the time per data item for a processor to transmit or receive a single data item to or from another processor; and let ![]() be the expected time per data item of executing the remaining filters i+1 through m, using the notation of equation (1). Also let m be the number of filters, n the initial number of data items on each processor, and R the number of processors. Perfect load rebalancing just after filter i will have a time advantage of:
be the expected time per data item of executing the remaining filters i+1 through m, using the notation of equation (1). Also let m be the number of filters, n the initial number of data items on each processor, and R the number of processors. Perfect load rebalancing just after filter i will have a time advantage of:
![]()
(This conservatively assumes the worst case of a bus architecture where all processors examine all ![]() transferred data items; but with a star processor architecture for instance, where every processor has a unique connection to every other processor, the most unbalanced processor determines rebalancing time, and
transferred data items; but with a star processor architecture for instance, where every processor has a unique connection to every other processor, the most unbalanced processor determines rebalancing time, and ![]() can be replaced by
can be replaced by ![]() .)
.)
As an example, take the one in the last section where we have 8000 data items, 16 processors, 500 items initially assigned to each processor, and a filter with success probability ![]() . There we found
. There we found ![]() and
and ![]() . Assume the time cost of the remaining filters per data item is
. Assume the time cost of the remaining filters per data item is ![]() and
and ![]() . Then
. Then ![]() which says rebalancing is advantageous.
which says rebalancing is advantageous.
In general, we can substitute equations (2) and (3) into (4) to obtain:
![]()
where ![]() is the standard deviation of the number of data items per processor after filter i. Rebalancing will only be desirable if this is positive, or if:
is the standard deviation of the number of data items per processor after filter i. Rebalancing will only be desirable if this is positive, or if:
![]()
These formulae hold for any number of filters m even if m<R for R the number of processors. They also hold for the total number of data items less than R. However, in the latter case the speedup obtained by parallelism for filter i is limited to the number of data items as input to i, although some partial compensation can be obtained then with the timestamp approach mentioned above.
5. An algorithm for load rebalancing
More than one rebalancing may help in a sequence of filters. But rebalancing reduces the need for subsequent rebalances in the filter sequence. In particular, if rebalancing is done just before filter i, the standard deviation of the number of items remaining after filter j on a processor changes from ![]() to
to ![]() . Since often this change has little effect, we can use a heuristic "greedy" algorithm to find the best rebalancing plan for a filter sequence:
. Since often this change has little effect, we can use a heuristic "greedy" algorithm to find the best rebalancing plan for a filter sequence:
This algorithm is ![]() m the number of filters.
m the number of filters.
As an example, suppose we have three filters in this order: filter 1 which requires 10 time units and has a success probability 0.1, filter 2 which requires 30 and has a success probability 0.05, and filter 3 which requires 8 and has a success probability of 0.5. Hence ![]() and
and ![]() . Assume 8000 initial data items assigned to 16 processors, so
. Assume 8000 initial data items assigned to 16 processors, so ![]() ,
, ![]() , and
, and ![]() . Then:
. Then:
![]()
Assume also that ![]() ,
, ![]() , and
, and ![]() . Then:
. Then:
![]()
![]()
Hence the best place to rebalance is after filter 1. If we do that,
![]() is changed to
is changed to ![]() and
and ![]() to:
to:
![]()
So we should rebalance only after filter 1 and not after filter 2.
The algorithm tries to anticipate the need to balance loads, but rebalancing can also be done at execution time when set sizes are unexpectedly large. To do this, use equation (4) to compute ![]() using the actual processor allocations for "maxdev" and "absdev"; rebalance if
using the actual processor allocations for "maxdev" and "absdev"; rebalance if ![]() . This entails a usually negligible overhead of
. This entails a usually negligible overhead of ![]() per filter.
per filter.
6. Experiments on the degree of load imbalance in simulated filtering
We first generated 5000 random filter sequences (created by the program in [8]) to study average-case performance of our methods. The program assigned to filters a random ![]() on the range 0.001 to 0.999. In one set of experiments, filter times were initially evenly distributed from 0 to 10; in another set, logarithms of times were evenly distributed from 0.01 to 0.99. But for both we occasionally increased the time of later filters as necessary to ensure that no filter took less than a preceding filter that it logically entailed. Since optimizing the filter sequence is important for realistic balancing analysis, we found the locally-optimal sequence using the heuristic methods of [8], methods which we showed there to almost always find the globally optimal sequence. We then computed two ratios for this sequence:
on the range 0.001 to 0.999. In one set of experiments, filter times were initially evenly distributed from 0 to 10; in another set, logarithms of times were evenly distributed from 0.01 to 0.99. But for both we occasionally increased the time of later filters as necessary to ensure that no filter took less than a preceding filter that it logically entailed. Since optimizing the filter sequence is important for realistic balancing analysis, we found the locally-optimal sequence using the heuristic methods of [8], methods which we showed there to almost always find the globally optimal sequence. We then computed two ratios for this sequence: ![]() , the ratio of the extra time incurred by never rebalancing the expected imbalances in the filter sequence to
, the ratio of the extra time incurred by never rebalancing the expected imbalances in the filter sequence to ![]() , the time if no imbalances ever occurred; and
, the time if no imbalances ever occurred; and ![]() , the ratio of the expected number of data items that must be shifted to always maintain perfect balance to the filter processing load
, the ratio of the expected number of data items that must be shifted to always maintain perfect balance to the filter processing load ![]() , the product of the initial number of data items and the number of filters. So
, the product of the initial number of data items and the number of filters. So ![]() measures the relative benefit of rebalancing and
measures the relative benefit of rebalancing and ![]() measures the relative cost of rebalancing; both are dimensionless quantities. We can rewrite equation (4) using them:
measures the relative cost of rebalancing; both are dimensionless quantities. We can rewrite equation (4) using them:
![]()
Table 1 shows some representative data for ![]() and
and ![]() , where the four right columns represent geometric means of
, where the four right columns represent geometric means of ![]() and
and ![]() over the 5000 points. We can make three observations from the Table. First, imbalance can increase processing time by up to 52 percent in these cases, and rebalancing actions can amount to 78 percent to the number of filtering actions, so imbalance analysis can be important. Second, rebalancing is more desirable with a uniform distribution of the logarithms of the times; that suggests that more uneven time distributions will show even more advantage. Third, rebalancing is most helpful when the number of data items is near to or less than the number of processors. Such cases are not trivial, however; important applications occur with small numbers of items and costly filters, as with the natural-language and image-processing filters in [8].
over the 5000 points. We can make three observations from the Table. First, imbalance can increase processing time by up to 52 percent in these cases, and rebalancing actions can amount to 78 percent to the number of filtering actions, so imbalance analysis can be important. Second, rebalancing is more desirable with a uniform distribution of the logarithms of the times; that suggests that more uneven time distributions will show even more advantage. Third, rebalancing is most helpful when the number of data items is near to or less than the number of processors. Such cases are not trivial, however; important applications occur with small numbers of items and costly filters, as with the natural-language and image-processing filters in [8].
|
No. of filters |
No. of processors |
No. of data items per processor |
|
|
|
|
|
3 |
4 |
32 |
0.081 |
0.037 |
0.090 |
0.037 |
|
4 |
4 |
32 |
0.113 |
0.047 |
0.129 |
0.049 |
|
5 |
4 |
32 |
0.141 |
0.047 |
0.165 |
0.049 |
|
6 |
4 |
32 |
0.164 |
0.044 |
0.196 |
0.045 |
|
7 |
4 |
32 |
0.185 |
0.039 |
0.224 |
0.041 |
|
8 |
4 |
32 |
0.198 |
0.035 |
0.244 |
0.036 |
|
9 |
4 |
32 |
0.210 |
0.031 |
0.264 |
0.033 |
|
10 |
4 |
32 |
0.217 |
0.028 |
0.270 |
0.030 |
|
3 |
64 |
2 |
0.142 |
0.590 |
0.174 |
0.601 |
|
4 |
64 |
2 |
0.200 |
0.752 |
0.243 |
0.779 |
|
5 |
64 |
2 |
0.246 |
0.743 |
0.314 |
0.777 |
|
6 |
64 |
2 |
0.285 |
0.695 |
0.376 |
0.726 |
|
7 |
64 |
2 |
0.321 |
0.627 |
0.428 |
0.659 |
|
8 |
64 |
2 |
0.342 |
0.566 |
0.468 |
0.591 |
|
9 |
64 |
2 |
0.366 |
0.505 |
0.505 |
0.532 |
|
10 |
64 |
2 |
0.381 |
0.443 |
0.522 |
0.472 |
|
3 |
4 |
2048 |
0.009 |
0.005 |
0.009 |
0.006 |
|
4 |
4 |
2048 |
0.013 |
0.006 |
0.013 |
0.007 |
|
5 |
4 |
2048 |
0.016 |
0.006 |
0.017 |
0.007 |
|
6 |
4 |
2048 |
0.018 |
0.006 |
0.020 |
0.007 |
|
7 |
4 |
2048 |
0.020 |
0.005 |
0.022 |
0.006 |
|
8 |
4 |
2048 |
0.022 |
0.005 |
0.025 |
0.006 |
|
9 |
4 |
2048 |
0.024 |
0.004 |
0.027 |
0.005 |
|
10 |
4 |
2048 |
0.024 |
0.004 |
0.027 |
0.005 |
|
3 |
64 |
128 |
0.016 |
0.081 |
0.017 |
0.093 |
|
4 |
64 |
128 |
0.022 |
0.103 |
0.025 |
0.120 |
|
5 |
64 |
128 |
0.027 |
0.103 |
0.031 |
0.121 |
|
6 |
64 |
128 |
0.031 |
0.096 |
0.038 |
0.113 |
|
7 |
64 |
128 |
0.036 |
0.085 |
0.043 |
0.100 |
|
8 |
64 |
128 |
0.038 |
0.076 |
0.047 |
0.090 |
|
9 |
64 |
128 |
0.040 |
0.069 |
0.050 |
0.080 |
|
10 |
64 |
128 |
0.042 |
0.062 |
0.052 |
0.072 |
Table 1: Example results of the first experiment
Our experiments can be summarized with regression formulae predicting ![]() and
and ![]() from the number of filters m, the logarithm of the number of processors log ( R ), and the logarithm of the number of starting data items log ( n ). These formulae permit us to quickly judge when load balancing by the algorithm is worthwhile using
from the number of filters m, the logarithm of the number of processors log ( R ), and the logarithm of the number of starting data items log ( n ). These formulae permit us to quickly judge when load balancing by the algorithm is worthwhile using ![]() and
and ![]() . The best models we obtained on 1152 data points were (with coefficients of determination of 0.988 and 0.959 respectively):
. The best models we obtained on 1152 data points were (with coefficients of determination of 0.988 and 0.959 respectively):
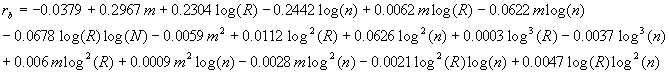
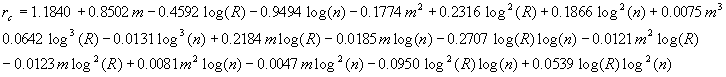
To test the importance of using the optimal filter sequence, we also ran experiments using the reverse of the optimal filter order and logarithmic times. This did improve the degree of balance, since ![]() decreased consistently to about 0.2 of its previous value, while
decreased consistently to about 0.2 of its previous value, while ![]() only increased to 1.2 of its previous value. But the time of executing the filter sequence increased on average by a factor of 7.0 for 5 filters and 24.9 for 10 filters, which seems a poor bargain.
only increased to 1.2 of its previous value. But the time of executing the filter sequence increased on average by a factor of 7.0 for 5 filters and 24.9 for 10 filters, which seems a poor bargain.
7. Experiments for a particular parallel machine
We also studied a real multiprocessor, the IRIS 3D/340, to see the effects of modest overheads on parallelism. (Again, many applications do not have such low overheads.) We did a filtering implementation with a master thread for the control processor which forked threads for the filtering processors. When a thread finished applying a filter to its share of data, it proceeds to the next filter, except if it had received an order directing it to suspend execution. Then the master thread assessed workloads, rebalanced them, and restarted the threads. Our runs provided a least-squares estimate of ![]() microseconds, R the number of processors; the rebalancing cost factor,
microseconds, R the number of processors; the rebalancing cost factor, ![]() , was observed to be negligible for this shared-memory machine. (The first fork is much more time-consuming than subsequent forks, but represents constant overhead for all execution plans.)
, was observed to be negligible for this shared-memory machine. (The first fork is much more time-consuming than subsequent forks, but represents constant overhead for all execution plans.)
Real-time filtering on the IRIS encountered performance variations due to uncontrollable operating system behavior and the presence of other users on the machines' network. So we opted to simulate the machine with parameters derived from the runs. Instead of random filter sequences unlikely to occur in applications, we used filter sequences like those found to be optimal in [8]. So we assumed the "work-spread" between filters, ![]() using the notation of Section 2, was approximately constant. Thus work-spread was a fourth input in these experiments besides the three of Table 1. For output we measured sequence-time speedup, the time when using one processor divided by the time when using all processors. We compared three approaches: (i) no rebalancing; (ii) heuristic rebalancing using the algorithm of Section 5; and (iii) optimal rebalancing, trying all
using the notation of Section 2, was approximately constant. Thus work-spread was a fourth input in these experiments besides the three of Table 1. For output we measured sequence-time speedup, the time when using one processor divided by the time when using all processors. We compared three approaches: (i) no rebalancing; (ii) heuristic rebalancing using the algorithm of Section 5; and (iii) optimal rebalancing, trying all ![]() ways of rebalancing and choosing the one of minimum time as predicted from equations (1) and (5).
ways of rebalancing and choosing the one of minimum time as predicted from equations (1) and (5).
Our experiments showed the work-spread parameter was most important in affecting balancing, and higher spreads caused higher imbalances. We also found (a) when more than 100 items were assigned to a processor, imbalance never ran more than 10 percent over optimum time; (b) otherwise, rebalancing was unnecessary if work-spread < 1.5; and (c) the need to rebalance was not significantly related to the number of filters. We also identified upper bounds on the benefit of rebalancing by analyzing filter sequences with optimal rebalancing assuming ![]() . We then focused on regions of the search space where the speed without rebalancing was more than 10 percent of the optimum. Confirming Table 1, imbalance was more significant when the number of items per processor was small and when the number of processors was large.
. We then focused on regions of the search space where the speed without rebalancing was more than 10 percent of the optimum. Confirming Table 1, imbalance was more significant when the number of items per processor was small and when the number of processors was large.
Figure 1 shows an example of our results for 32 processors and 4 independent filters, and displays the ratio of the speedup obtained by parallelizing without rebalancing versus parallelizing with rebalancing using the heuristic algorithm. The plot shows a 100 percent improvement for 32 items per processor, and up to 25 percent for 256 items per processor. In these experiments, heuristic rebalancing was no worse than 1 percent more than optimal rebalancing. To test sensitivity to the cost of overhead, we also ran the heuristic with the same cases and with ![]() set to 100 times the average IRIS values. Figure 2 shows the ratio of the subsequent heuristic speedup to the original heuristic speedup, and shows only minor differences. This suggests that the heuristic algorithm would still be suitable with significant communication overheads, as for a cluster of workstations.
set to 100 times the average IRIS values. Figure 2 shows the ratio of the subsequent heuristic speedup to the original heuristic speedup, and shows only minor differences. This suggests that the heuristic algorithm would still be suitable with significant communication overheads, as for a cluster of workstations.
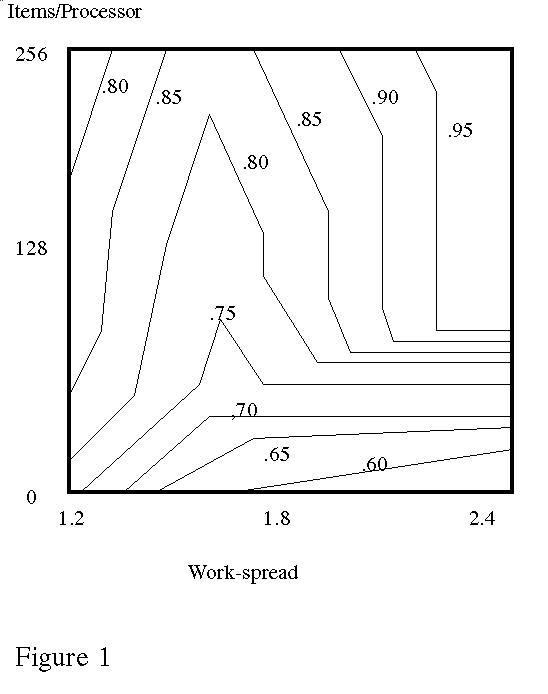
Figure 1: Ratio of speedup when parallelizing without load rebalancing to speedup when the rebalancing heuristic is employed (32 processors, 4 filters, empirically-obtained load-balancing times).
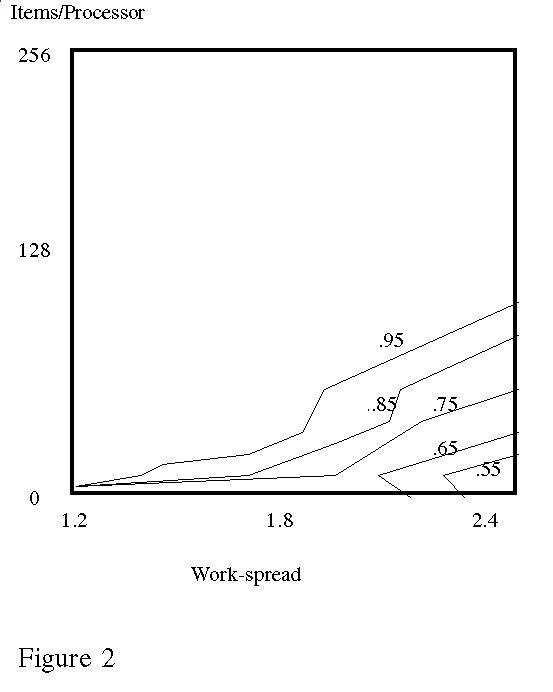
Figure 2: Ratio of heuristic speedup when load rebalancing time is increased 100 times to (32 processors and 4 filters).
Overall, results of the IRIS experiments suggest that that our heuristic algorithm is useful for medium scale multiprocessing (16-64 processors). For fewer processors, parallel filtering remains reasonably well balanced. For more processors, rebalancing seems likely to cost more than its benefits.
8. Extending the model to variable-time filters
We have so far assumed that filter time is a constant per data item. This is appropriate when filters are implemented by hash lookups, by searches in trees in which all leaves are at the same level, or when the result of a numeric calculation without conditionals is compared to a threshold. But if filter processing time can vary, processor imbalance increases and thus the advantages of rebalancing. This requires a new formula for "maxdev" in equation (4); the "absdev" formula is unchanged.
We again used Monte Carlo methods on sets of now 1024 random variables to get an approximate formula for "maxdev", now generating a random variable x for the ratio of filter execution time per data item to its expected value. We assumed that x was normally distributed about 1 with standard deviation s and with (assumed rare) truncation at 0. Then the random variable y for the average of k values of x will have approximately a normal distribution with ![]() times less standard deviation:
times less standard deviation:
![]()
Our experiments used the n, p, and R values of Section 3 and took ![]() for
for ![]() to
to ![]() . The best model that we found relating s and the old "maxdev" (from equation (2)) to the new "maxdev" (by regression on the square of maxdev) was:
. The best model that we found relating s and the old "maxdev" (from equation (2)) to the new "maxdev" (by regression on the square of maxdev) was:
![]()
Again, we explored a variety of additional factors, but none added anything significant. This model had a coefficient of determination of 0.932, not bad for a fit to 6144 points representing extrema of a random variable. These results were for s<1, if s continues to increase, the normal distribution assumption no longer always holds, but in the limit maxdev should increase proportionately to s.
As an example, take the three-filter case of Section 5 with the rebalancing after filter 1. Now assume that filter 2 is a lookup in a nonuniform index in which data can be at a depth of 1, 2, or 3. Assume with probability 0.25 that processing takes 1 unit of time, probability 0.5 that it takes 2 units, and probability 0.25 it takes 3 units. Then the standard deviation of random variable x is ![]() . Hence:
. Hence:
![]() .
.
![]()
Substituting in equation (4):
![]()
Hence rebalancing after filter 2 has become desirable even with rebalancing after filter 1.
9. Conclusions
We have shown that data parallelism is the best way to take advantage of multiple processors for an information filtering problem. We have provided the reader with quick practical tools for measuring the degree of imbalance that can occur in data-parallel filtering in equation (5) or the combination of equations (4) and (7). For handling large numbers of filters, the algorithm of Section 5 will help. Two kinds of experiments, general ones and those focused on a particular architecture, have confirmed our analysis. Careful load balancing can be important when communications or filter costs are high, and a quick way to evaluate it can be valuable.
References
[1] N. J. Belkin and W. B. Croft, "Information Filtering and Information Retrieval: Two Sides of the Same Coin?," Communications of the ACM, Vol. 35, No. 12, December 1992, pp. 29-38.
[2] G. Dahlquist and A. Bjorck, Numerical Methods, Prentice-Hall, Englewood Cliffs, N. J., 1974.
[3] J. De Keyser and D. Roose, "Load Balancing Data Parallel Programs on Distributed Memory Computers," Parallel Computing, Vol. 19, 1993, pp. 1199-1219.
[4] C. Faloutsos, "Signature-Based Text Retrieval Methods: A Survey," Database Engineering, March 1990, pp. 27-34.
[5] M. Jarke and J. Koch, "Query Optimization in Database Systems," Computing Surveys, Vol. 16, No. 2, June 1984, pp. 117-157.
[6] D. Nicol and P. Reynolds, "Optimal Dynamic Remapping of Data Parallel Computations," IEEE Transactions on Computers, Vol. 39, No. 2, February 1990, pp. 206-219.
[7] K. Pattipatti and M. Dontamsetty, "On a Generalized Test Sequencing Problem," IEEE Transactions on Systems, Man, and Cybernetics, Vol. 22, No. 2, March/April 1992, pp. 392-396.
[8] N. C. Rowe, "Using Local Optimality Criteria for Efficient Information Retrieval with Redundant Information Filters," ACM Transactions on Information Systems, Vol. 14, No. 2, April 1996, pp. 138-174.
[9] N. C. Rowe, "Preicse and Efficient Retrieval of Captioned Images: The MARIE Project," Library Trends, Vol. 48, No. 2, Fall 1999, pp. 475-495.
[10] C. Stanfill and B. Kahle, "Parallel Free-Text Search on the Connection Machine System," Communications of the Association for Computing Machinery, Vol. 29, No. 12, December 1986, pp. 1229-1239.
[11] H. Stone, High-Performance Computer Architecture, Addison-Wesley, Reading, Mass., 1987.
Acknowledgements: This work was sponsored by DARPA as part of the I3 Project under AO 8939, and by the U. S. Naval Postgraduate School under funds provided by the Chief for Naval Operations. Computations were done with Mathematica software.