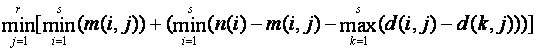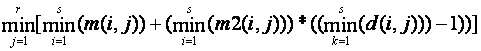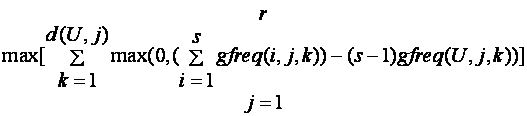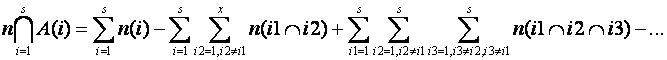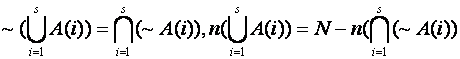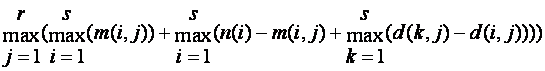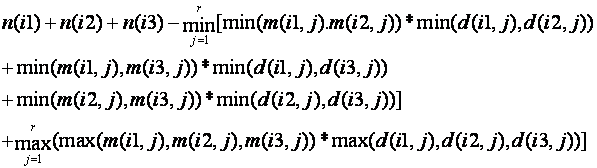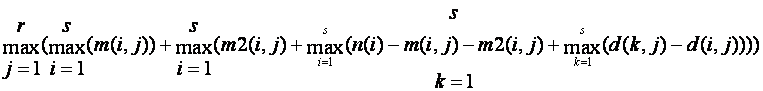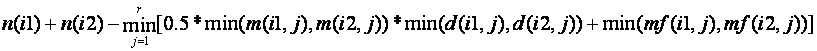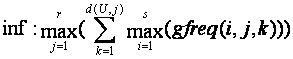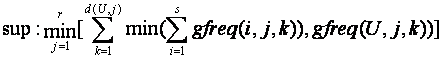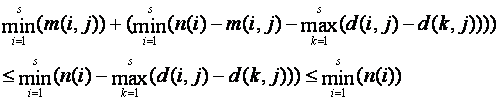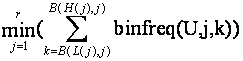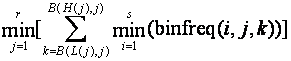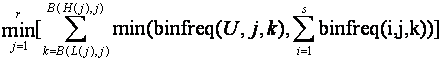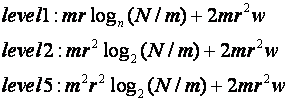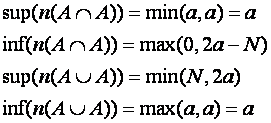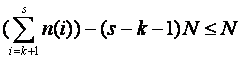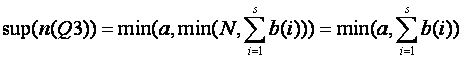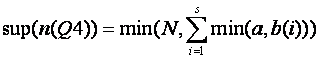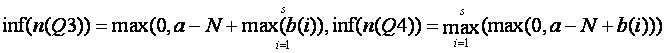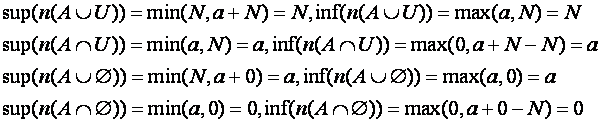Absolute bounds on set intersection and union sizes from distribution information
Neil C. Rowe
Department of Computer Science
Code 52 Naval Postgraduate School Monterey, CA 93943
Abstract
Estimation of set intersection and union sizes is important for access method selection for a database and other data retrieval problems. Absolute bounds on sizes are often easier to compute than estimates, requiring no distributional or independence assumptions, and can answer many of the same needs. We present a catalog of quick closed-form bounds on set intersection and union sizes; they can be expressed as rules, and managed by a rule-based system architecture. These methods use a variety of statistics precomputed on the data, and exploit homomorphisms (onto mappings) of the data items onto distributions that can be more easily analyzed. The methods can be used anytime, but tend to work best when there are strong or complex correlations in the data. This circumstance is poorly handled by the standard independence-assumption and distributional-assumption estimates, and hence our methods fill a need.
Keywords: intersection, union, databases, query processing, statistical computing, statistical databases, inequalities, sets, Boolean algebra, estimation, frequency distributions. This paper appeared in IEEE Transactions on Software Engineering, SE-14, no. 7 (July 1988), 1033-1048. The equations were redrawn in 2008.
1. Why bounds?
Good estimation of the sizes of set intersections and unions is crucial to selection of efficient access methods for data in a database, especially when joins are involved. Such estimation is necessary for estimates of paging or blocks required. But often absolute bounds on such sizes can serve the purpose of estimates, for several reasons:
1. Absolute bounds are more often possible to compute than estimates. Estimates generally require distributional assumptions about the data, assumptions that are sometimes difficult and awkward to verify, particularly for data subsets not much studied. Bounds require no assumptions.
2. Bounds are often easier to compute than estimates, because the mathematics, as we shall see, can be based on simple principles -- rarely are integrals (possibly requiring numerical approximation) needed as with distributions. This has long been recognized in computer science, as in the analysis of algorithms where worst-case (or bounds) analysis tends to be much easier than average-case.
3. Even when bounds tend to be weak, several different bounding methods may be tried and the best bound used. This paper gives some quite different methods that can be used on the same problems.
4. Bounds fill a gap in the applicability of set-size determination techniques. Good methods exist when one can assume independence of the attributes of a database, and some statistical techniques exist when one can assume strong but simple correlations between attributes. But until now there have been few techniques for situations with many and complicated correlations between attributes, situations bounds can address. Such circumstances occur more with human-generated data than natural data, so with increasing computerization of routine bureaucratic activity we may see more of them.
5. Since choices among database access methods are absolute (yes-or-no), good bounds on the sizes of intersections can sometimes be just as helpful for making decisions as "reasonable-guess" estimates, when the bounds do not substantially overlap between alternatives.
6. Bounds in certain cases permit absolutely certain elimination (pruning) of possibilities, as in branch-and-bound algorithms and in compilation of database access paths. Bounds also help random sampling obtain a sample of fixed size from an unindexed set whose size is not known, since an error retrieving too few items is much worse than an error retrieving too many.
7. Bounds also provide an idea of the variance possible in an estimate, often more easily than a standard deviation. This is useful for evaluating retrieval methods, since a method with the same estimated cost as another, but tighter bounds, is usually preferable.
8. Sizes of set intersections are also valuable in their own right, particularly with "statistical databases" [16], databases designed primarily to support statistical analysis. If the users are doing "exploratory data analysis" [18], the early stages of statistical study of a data set, quick estimates are important and bounds may be sufficient. This was the basis of an entire statistical estimation system using such "antisampling" methods [14].
9. Bounds (and especially bounds on counts) are essential for analysis of security of statistical databases from indirect inferences [5].
As with estimates, precomputed information is necessary for bounds on set sizes. The more space allocated to precomputed information, the better the bounds can be. Unlike most work with estimates, however, we will exploit prior information besides set sizes, including extrema, frequency statistics, and fits to other distributions. We will emphasize upper bounds on intersection sizes, but we will also give some lower bounds, and also some bounds on set unions and complements.
Since set intersections must be defined within a "universe" U, and we are primarily interested in database applications, we will take U to be a relation of a relational database. Note that imposing selections or restrictions on a relation is equivalent to intersecting sets of tuples defining those selections. Thus, our results equivalently bound the sizes of multiple relational-database selections on the same relation.
Section 2 of this paper reviews previous research, and Section 3 summarizes our method of obtaining bounds. Section 4 examines in detail the various frequency-distribution bounds, covering upper bounds on intersections (section 4.1), lower bounds on intersections (section 4.2), bounds on unions (section 4.4), bounds on arbitrary Boolean expressions for sets (section 4.6), and concludes (section 4.7) with a summary of storage requirements for these methods. Section 5 evaluates these bounds both analytically and experimentally. Section 6 examines a different but analogous class of bounds, range-analysis, first for univariate ranges (section 6.1), then multivariate (section 6.2).
1. Previous work
Analysis of the sizes of intersections is one of several critical issues in optimizing database query performance; it is also important in optimizing execution of logic-programming languages like Prolog. The emphasis in previous research on this subject has been almost entirely on developing estimates, not bounds. Various independence and uniformity assumptions have been suggested (e.g., [4] and [11]). These methods work well for data that has no or minor correlations between attributes and between sets intersected, and where bounds are not needed.
Christodoulakis [2] (work extending [9]) has estimated sizes of intersections and unions where correlations are well modeled probabilistically. He uses a multivariate probability distribution to represent the space of possible combinations of the attributes, each dimension corresponding to a set being intersected and the attribute defining it. The size of the intersection is then the number of points in a hyperrectangular region of the distribution. This approach works well for data that has a few simple but possibly strong correlations between attributes or between sets intersected, and where bounds are not needed. Its main disadvantages are (1) it requires extensive study of the data beforehand to estimate parameters of the multivariable distributions (and the distributions can change with time and later become invalid), (2) it only exploits count statistics (what we call level 1 and level 5 information in section 4), and (3) it only works for databases without too many correlations between entities.
Similar work is that of [7]. They model the data by coefficients equivalent to moments. They do not use multivariate distributions explicitly, but use the independence assumption whenever they can. Otherwise they partition the database along various attribute ranges (into what they call "betas", what [5] calls "1-sets", and what [12] calls "first-order sets") and model the univariate distributions on every attribute. This approach does allow modeling of arbitrary correlations in the data, both positive and negative, but requires potentially enormous space in its reduction of everything to univariate distributions. It can also be very wasteful of space, since it is hard to give different correlation phenomena different granularities of description. Again, the method exploits only count statistics and only gives estimates, not bounds.
Some relevant work involving bounds on set sizes is that of [8], which springs from a quite different motivation that ours (handling of incomplete information in a database system), and again only uses count statistics. [10] investigates bounds on the sizes of partitions of a single numeric attribute using prior distribution information, but does not consider the much more important case of multiple attributes.
There has also been relevant work over the years on probabilistic inequalities [1]. We can divide counts by the size of the database to turn them into probabilities on a finite universe, and apply some of these mathematical results. However, the first and second objections of section 1 apply to this work: it usually makes detailed distributional assumptions, and is mathematically complex. For practical database situations we need something more general-purpose and simpler.
3. The general method
We present two main approaches to calculation of absolute bounds on intersection and union sizes in this paper.
Suppose we have a census database on which we have tabulated statistics of state, age, and income. Suppose we wish an upper bound on the number of residents of Iowa that are between the ages of 30 and 34 inclusive, when all we know are statistics on Iowa residents and statistics on people age 30-34 separately. One upper bound would be the frequency of the mode (most common) state for people age 30-34. Another would be five times the frequency of the most common age for people living in Iowa (since there are five ages in the range 30-34). These are examples of frequency-distribution bounds (discussed in section 4), to which we devote primary attention in this paper.
Suppose we also have income information in our database, and suppose the question is to find the number of Iowans who earned over 100,000 dollars last year. Even though the question has nothing to do with ages, we may be able to use age data to answer this question. We obtain the maximum and minimum statistics on the age attribute of the set of Americans who earned over 100,000 dollars (combining several subranges of earnings to get this if necessary), and then find out the number of Americans that lie in that age range, and that is an upper bound. We can also use the methods of the preceding paragraph to find the number of Iowans lying in that age range. This is an example of range-restriction bounds (discussed in section 6).
Our basic method for both kinds of bounds is quite simple. Before querying any set sizes, preprocess the data:
(1) Group the data items into categories. The categories may be arbitrary.
(2)Count the number of items in each category, and store statistics characterizing (in some way) these counts.
Now when bounds on a set intersection or union are needed:
(3) Look up the statistics relevant to all the sets mentioned in the query, to bound certain subset counts.
(4) Find the minima (for intersections) or maxima (for unions) of the corresponding counts for each subset.
(5) Sum up the minima (or maxima) to get an overall bound on the intersection size.
All our rules for bounds on sizes of set intersections will be expressed as hierarchy of different "levels" of statistics knowledge about the data. Lower levels mean less prior knowledge, but generally poorer bounding performance.
The word "value" may be interpreted as any equivalence class of data attribute values. This means that prior counts on different equivalence classes may be used to get different bounds on the same intersection size, and the best one taken, though we do not include this explicitly in our formulae.
4. Frequency-distribution bounds
We now examine bounds derived from knowledge (partial or complete) of frequency distributions of attributes.
4.1 Upper frequency-distribution bounds
4.1.1 Level 1: set sizes of intersected sets only
If we know the sizes of the sets being intersected, an upper bound
("sup") on the size of the intersection is obviously 
where n(i)
is the size of the ith set and s is the number of sets.
4.1.2 Level 2a: mode frequencies and numbers of distinct values
Suppose we know the mode (most common) frequency m(i,j) and number of
distinct values d(i,j) for some attribute j for each set i of s total. Then an
upper bound on the size of the intersection is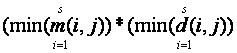 
. To prove this: (1)
an upper bound on the mode frequency of the intersection is the minimum of the
mode frequencies; (2) an upper bound on the number of distinct values of the
intersection is the minimum of the number for each set; (3) an upper bound on
the size of a set is the product of its mode frequency and number of distinct
values; and (4) an upper bound on the product of two nonnegative uncertain
quantities is the product of their upper bounds.
If we know information about more than one attribute of the data, we can
take the minimum of the upper bound computations on each attribute. Letting r
be the number of attributes we know these statistics about, the revised bound
is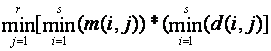 
.
A special case occurs when one set being intersected has only one possible value on a given attribute--that is, the number of distinct values is 1. This condition can arise when a set is defined as a partition of the values on that attribute, but also can occur accidentally, particularly when the set concerned is small. Hence the bound is the first of the inner minima, or the minimum of the mode frequencies on that attribute. For example, an upper bound on the number of American tankers is the mode frequency of tankers with respect to the nationality attribute.
The second special case is the other extreme, when one set being intersected has all different values for some attribute, or a mode frequency of 1. This arises from what we call an "extensional key" ([12], ch. 3) situation, where some attribute functions like a key to a relation but only in a particular database state. Hence the first bound is the minimum of the number of distinct values on that attribute. For example, an upper bound on the number of American tankers in Naples, when we happen to know Naples requires only one ship per nationality at a time, is the number of different nationalities for tankers at Naples.
4.1.3 Level 2b: a different bound with the same information
A different line of reasoning leads to a different bound utilizing mode
frequency and number of distinct values, an "additive" bound instead
of the "multiplicative" one above. Consider the mode on some
attribute as partitioning a set into two pieces, those items having the mode
value of the attribute, and those not. Then a bound on the size of the
intersection of r sets is 
.
To prove this, let 
be the everything in set i
except for its mode, and consider three cases. Case 1: assume the set i that
satisfies the first inner min above also satisfies the second inner min. Then
the expression in brackets is just the size of this set. But if such a set has
minimum mode frequency and minimum-size , it must be the smallest set.
Therefore its size must be an upper bound on the size of the intersection.
Case 2: assume set i satisfies the first inner min, some other set j
satisfies the second inner min, and sets i and j have the same mode (most
common value). We need only consider these two sets, because an upper bound on
their intersection size is an upper bound on the intersection of any group of
sets containing them. Then the minimum of the two mode frequencies is an upper
bound on the mode frequency of the intersection, and the minima of the sizes of
and
is
an upper bound on the R for the intersection. Thus the sum of two minima on s
is a minimum on s.
Case 3: assume set i satisfies the first inner min, set j satisfies the
second inner min, and i and j have different modes. Let the mode frequency of i
be a and that of j be d; suppose the mode of i has frequency e in set j, and
suppose the rest of j (besides the d+e) has total size f. Furthermore suppose
that the mode of j has frequency b in set i, and the rest of i (besides the
a+b) has total count c. Then the 2b bound above is a+e+f. But in the actual
intersection of the two sets, a would match with e, b with d, and c with f,
giving an upper bound of min(a,e)+min(b,d)+min(c,f). But 
, and lastly 
because 
. Hence our 2b
bound is an upper bound on the actual intersection size.
But the above bound doesn't use the information about the number of distinct values. If the set i that minimizes the last minima in the formula above contains more than the minimum of the number of distinct values d(i,j) over all the sets, we must "subtract out" the excess, assuming conservatively that the extra values occur only once in set i:
It would seem that we could do better by subtracting out the minimum mode frequency the sets a number of times corresponding to the minima of the number of distinct values over all the sets. However, this reduces to the level 2a bound.
4.1.4 Level 2c: Diophantine inferences from sums
A different kind of information about a distribution is sometimes useful when the attribute is numeric: its sum and other moments on the attribute for the set. (Since the sum and standard deviation require the same amount of storage as level 2a and 2b information, we call them another level 2 situation.) This information is only useful when (a) we know the set of all possible values for the universal set, and (b) there are few of these values relative to the size of the sets being intersected. Then we can write a linear Diophantine (integer-solution) equation in unknowns representing the number of occurrences of each particular numeric value in each of the sets being intersected, and each solution represents a possible partition of counts on each value. An upper bound on the intersection size is thus the sum over all values of the minimum over all sets of the maximum number of occurrences of a particular value for a particular set. See [13] for a further discussion of Diophantine inferences about statistics. A noteworthy feature of Diophantine equations is the unpredictability of their number of solutions.
4.1.5 Level 3a: other piecemeal frequency distribution information
The level 2 approach will not work well for sets and attributes that have relatively large mode frequencies. We could get a better (i.e. lower) upper bound if we knew the frequencies of other values than the mode. Letting m2(i,j) represent the frequency of the second most common value of the ith set on the jth attribute, a bound is:
For this we can prove by contradiction that the frequency of the second most common value of the intersection cannot occur more than the minimum of the frequencies of the second most common values of those sets. Let M be the mode frequency of the intersection and let M2 be the frequency of the second most common value in the intersection. Assume M2 is more than the frequency of the second most common value in some set i. Then M2 must correspond to the mode frequency of that set i. But then the mode frequency of the intersection must be less than or equal to the frequency of the second most frequent value in set i, which is a contradiction.
For knowledge of the frequency of the median-frequency value (call it mf(i,j)), we can just divide the outer minimum into two parts (assuming the median frequency for an odd number of frequencies is the higher of the two frequencies it theoretically falls between):
The mean frequency is no use since this is always the set size divided by the number of distinct values.
4.1.6 Level 3b: a different bound using the same information
In the same way that level 2b complements level 2a, there is a 3b upper bound that complements the preceding 3a bound:
(Here we don't include the median frequency because an upper bound on this for an intersection is not the minimum of the median frequencies of the sets intersected.) The formula can be improved still further if we know the frequency of the least common value on set i, and it is greater than 1: just multiply the maximum of (d(i,j)-d(k,j)) above by this least frequency for i before taking the minimum.
4.1.7 Level 4a: full frequency distribution information
An obvious extension is to knowledge of the full frequency distribution (histogram) for an attribute for each set, but not which value has which frequency. By similar reasoning to the last section the bound is:
where freq(i,j,k) is the frequency of the kth most frequent value of the ith set on the jth attribute. This follows from recursive application of the first formula for a level-2b bound. First we decompose the sets into two subsets each, for the mode and non-mode items; then we decompose the non-mode subsets into two subsets each, for .I their mode and non-mode items; and so on until the frequency distributions are exhausted.
We can still use this formula if all we know is an upper bound on the actual distribution--we just get a weaker bound. Thus there are many gradations between level 3 and level 4a. This is useful because a classical probability distribution (like a normal curve) that lies entirely above the actual frequency distribution can be specified with just a few parameters and thus be stored in very little space.
As an example, suppose we have two sets characterized by two exponential
distributions of numbers between 0 and 2. Suppose we can upper-bound the first
distribution by 
and
the second by 
,
so there are about 86 of each set. Then the distribution of the set intersection
is bounded above by the minimum of those two distributions. So an upper bound
on the size of the intersection is
4.1.8 Level 4b: Diophantine inferences about values
A different kind of Diophantine inference than that discussed in 4.1.4 can arise when the data distribution is known for some numeric attribute. We may be able to use the sum statistic for set values on that attribute, plus other moments, to infer a list of the only possible values for each set being intersected; then the possible values for the intersection set must occur in every possibility list. We can use this to upper-bound size of the intersection as the product of an upper bound on the mode frequency of the intersection and the number of possible values of the intersection. To make this solution practical we require that (a) the number of distinct values in each set being intersected is small with respect to the size of the set, and (b) the least common divisor of the possible values be not too small (say less than .001) of the size of the largest possible value. Then we can write a linear Diophantine equation in unknowns which this time are the possible values, and solve for all possibilities. Again, see [13] for further details.
4.1.9 Level 5: tagged frequency distributions
Finally, the best kind of frequency-distribution information we could have about sets would specify exactly which values in each distribution have which frequencies. This gives an upper bound of:
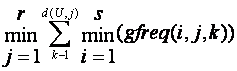
where gfreq(i,j,k) is the frequency of globally-numbered value k of attribute j for set i, which is zero when value k does not occur in set i, and where d(U,j) is the number of distinct values for attribute j in the data universe U.
All that is necessary to identify values is a unique code, not necessarily the actual value. Bit strings can be used together with an (unsorted) frequency distribution of the values that do occur at least once. Notice that level 5 information is analogous to level 1 information, as it represents sizes of particular subsets formed by intersecting each original set with the set of all items in the relation having a particular value for a particular attribute. This is what [12] calls "second-order sets" and [5] "2-sets". Thus we have come full circle, and there can be no "higher" levels than 5.
4.2 Lower bounds from frequency distributions
On occasion we can get nonzero lower bounds ("inf") on the size of a set intersection, when the size of the data universe U is known, and the sets being intersected are almost its size.
4.2.1 Lower bounds: levels 1 and 5
A set intersection is the same as the complement (with respect the universe) of the set union of the complements. An upper bound on the union of some sets is the sum of their set sizes. Hence a lower bound on the size of the intersection, when the universe U is size N, is
which is the statistical form of the simplest case of the Bonferroni inequality. For most sets of interest to a database user this will be zero since the sum is at most sN. But with only two sets being intersected, or sets corresponding to weak restrictions (that is, sets including almost all the universe except for a few unusual items, sets intersected with others to get the effect of removing those items), a nonzero lower bound may more often occur.
For level 5 information the bound is:
where gfreq(i,j,k) is as before the number of occurrences of the kth most common value of the jth attribute for the ith set, U is the universe set, and d(U,j) is the number of distinct values for attribute j among the items of U.
4.2.2 Lower bounds: levels 2, 3, and 4
It is more difficult to obtain nonzero lower bounds when statistical
information is not tagged to specific sets, as for what we have called levels
2, 3, and 4. If we know the mode values as well as the mode frequencies, and
the modes are all identical, we can bound the frequency of the mode in the
intersection by the analogous formula to level 1 above, using the mode
frequency of the universe (if the mode is identical) for N. Without mode
values, we can infer that modes are identical for some large sets, whenever for
each 
where
m(i,j) is the mode frequency of set i on attribute j, m2(i,j) the frequency of
the second most common value, n(i) the size of set i, and N the size of the
data universe.
The problem for level 4 lower bounds is that we do not know which
frequencies have which values. But if we have some computer time to spend, we
can exhaustively consider combinatorial possibilities, excluding those
impossible given the frequency distribution of the universe, and take as the
lower bound the lowest level-5 bound. For instance, with an implementation of
this method in Prolog, we considered a universe with four data values for some
attribute, where the frequency distribution of the universe was (54, 53, 52,
51), and the frequency distributions of the two sets intersected were (40, 38,
22, 20) and (30, 23, 21, 16). The level 4a lower bound was 8, and occurred for
several matchings, including (54-38-21,53-40-16,52-22-30,51-20-23).
The level 1 lower bound is 210 - 120 - 90 = 0, so the effort may be worth it.
(The level 1 and 4 upper bounds are both 30 + 23 + 21 + 16 = 90.) But the number
of combinations that must be considered for k distinct values in the universe
is 
.
4.2.3 Definitional sets
Another very different way of getting lower bounds is from knowledge of how the sets intersected were defined. If we know that set i was defined as all items having particular values for an attribute j, then in analyzing an intersection including set i, the "definitional" set i contributes no restrictions on attributes other than j and can be ignored. This is redundant information with levels 1 and 5, but it may help with the other levels. For instance, for i1 definitional on attribute j, a lower bound on the size of the intersection of sets i1 and i2 is the frequency of the least frequent value (the "antimode") of set i2 on j.
4.3 Better bounds from relaxation on sibling sets
Both upper and lower bounds can possibly be improved by relaxation among related sets in the manner of [3], work aimed at protection of data from statistical disclosure. This requires a good deal more computation time than the closed-form formulae in this paper and requires sophisticated algorithms. Thus we do not discuss it here.
4.4 Set unions
Rules analogous to those for intersection bounds can be obtained for union bounds. Most of these are lower bounds.
4.4.1 Defining unions from intersections
Since 
where
means
the size of the union of set i and set j, and 
means the size of their
intersection, extending our previous notation for set size, it follows that
using the distribution of intersection over union, and
Another approach to unions is to use complements of sets and DeMorgan's Law:
The problem with using this is the computing of statistics on the complement of a set, something difficult for level 2, 3, and 4 information.
In one important situation the calculation of union sizes is particularly easy: when the two sets unioned are disjoint (that is, their intersection is empty). Then the size of the union is just the sum of the set sizes, by the first formula in this section. Disjointness can be known a priori, or we can infer it using methods in section 6.1.2.
4.4.2 Level 1 information for unions
To obtain union bounds rules from intersection rules, we can do a "compilation" of the above formulae (section 3.5.5 of [12] gives other examples of this process) by substituting rules for intersections in them, and simplifying the result. Substituting the level 1 intersection bounds in the above set-complement formula:
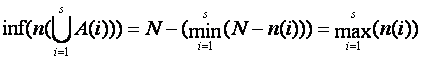
Here we use the standard notation of "inf" for the lower bound and "sup" for the upper bound.
4.4.3 Level 2b unions
If we know the mode frequency m(i,j) and the number of distinct values d(i,j) on attribute j, then we can use a formula analogous to the level 2b intersection upper bound, a lower bound on the union:
4.4.4 Level 2a unions
The approach used in level 2a for intersections is difficult to use here. We
cannot use the negation formula to relate unions to intersections because there
is no comparable multiplication of two quantities (like mode frequency and number
of distinct values) that gives a lower bound on something. However, for two
sets we can use the other (first) formula relating unions to intersections, to
get a union lower bound: 
For three sets, it becomes:
The formulae get messy for more sets.
4.4.5 Level 3b unions
Analogous to level 2b, we have the lower bound
where m2(i,j) is the frequency of the second most common value of set i on attribute j. And if we know the frequency of the least common value in set i, we multiply the maximum of (d(k,j)-d(i,j)) above by it before taking the maximum.
4.4.6 Level 3a unions
Analogous to level 2a, and to level 3a intersections, we have for the union of two sets a lower bound of:
where m2 is the frequency of the second most common value, and mf the frequency of the median-frequency value.
4.4.7 Level 4 unions
The analysis of level 4 is analogous to that of level 4 above, giving a lower bound of
where freq(i,j,k) is the frequency of the kth most frequent value of the ith set unioned on the jth attribute.
4.4.8 Level 5 unions
Level 5 is analogous to level 1:
4.5 Complements
To complete our coverage of set algebra we need set complements. The size of a complement is just the difference of the size N of the universe U (something that is often important, so we ought to know it) and the size of the set. An upper bound on a complement is N minus a lower bound on the size of the set; a lower bound on a complement is N minus an upper bound on the size of the set.
4.6 Embedded set expressions
So far we have only considered intersections, unions, and complements of simple sets about which we know exact statistics. But if the set-description language permits arbitrary embedding of query expressions, new complexities arise.
One problem is that the formulae of sections 4.1-4.4 require exact values for statistics, and such statistics are usually impossible for an embedded expression. But we can substitute upper bounds on the embedded-expression statistics in upper-bound formulae (or lower bounds when preceded in the formula by a minus sign). Similarly, we can substitute lower bounds on the statistics in lower-bound formulae (or upper bounds when preceded in the formula by a minus sign). This works for statistics on counts, mode frequency, frequency of the second-most common value, and number of distinct items--but not the median frequency.
4.6.1 Summary of equivalences
Another problem is that there can be many equivalent forms of a Boolean-algebra expression, and we have to be careful which equivalent form we choose because different forms give different bounds. Appendix A surveys the effect of various equivalences of Boolean algebra on bounds using level 1 information. Commutativity and associativity do not affect bounds, but factoring out of common sets in conjuncts or disjuncts with distributive laws is important since it usually gives better bounds and cannot worsen them. Factoring out enables other simplification laws which usually give better bounds too.
The formal summary of Appendix A is in Figure 1 ("yes" means
better in all but trivial cases). Since these transformations are sufficient to
derive set expression equivalent to another a set expression, the information
in the table is sufficient to determine whenever one expression is always
better than another.
4.6.2 The best form of a given set expression, for level 1 information
So the best form for the best level 1 bounds is a highly factored form, quite different from a disjunctive normal form or a conjunctive normal form. The number of Boolean operators doesn't matter, more the number of sets they operate on, so we don't want the "minimum-gate" form important in classical Boolean optimization techniques like Karnaugh maps. So minimum-term form [6] seems to be closest to what we want; note that all the useful transformations in the above table reduce the number of terms in an expression. Minimum-term form makes sense because multiple occurrences of the same term should be expected to cause suboptimal bounds arising from failure to exploit the perfect correlation of items in the occurrences. Unfortunately, the algorithms in [6] for transforming a Boolean expression to this form are considerably more complicated than the one to a minimum-gate form.
Minimum-term form is not unique. Consider these three equivalent expressions:
These cannot be ranked in a fixed order, though they are all preferable (by their use of a distributive law) to the unfactored equivalent
So we may need to compute bounds on each of several minimum-term forms, and take the best bounds. This situation should not arise very often, because users will query sets with few repeated mentions of the same set--parity queries are rarely needed.
Another problem with the minimum-term form is that it does not always give optimal bounds. For instance, let set A in the above be the union of two new sets D and E. Let the sizes of B, C, D, and E respectively be 10, 7, 7, and 8. Then the three factored forms give upper bounds respectively of min(15,17)+min(10,7) = 22, min(10,22) + min(15 ,7 ) = 17, and min(7,25) + min (15,10 ) = 17. But the first form is the minimum-term form, with 6 terms instead of 7. However, this situation only arises when there are different ways to factor, and can be forestalled by calculating a bound separately for the minimum-term form corresponding to every different way of factoring.
4.6.3 Embedded expression forms with other levels of information
Level 5 is analogous to level 1--it just represents a partition of all the sets being intersected into subsets of a particular range of values on a particular attribute, with bounds being summed up on all such ranges of values of the attribute. Thus the above "best" forms will be equally good for level 5 information. Analysis is considerably more complicated for levels 2, 3, and 4 since we do not have both upper and lower bounds in those cases. But the best forms for level 1 can be used heuristically then.
4.7 Analysis of storage requirements
4.7.1 Some formulae
Assume a universe of r attributes on N items, each attribute value requiring an average of w bits of storage. The database thus requires rNw bits of storage. Assume we only tabulate statistics on "1-sets" [5] or "first-order sets" [12] or universe partitions by the values of single attributes. Assume there are m approximately even partitions on each attribute. Then the space required for storage of statistics is as follows:
Level 1: there are mr sets with just a set size tabulated for each. Each set size should average about N/m, and should require about
bits, so a total of
bits are required. This will tend to be considerably less than rNw, the size of the database, because w will likely be on the same order as
Level 2: for each of the mr sets we have 2r statistics (the mode frequency and number of distinct values for each attribute). (This assumes we do not have any criteria to claim certain attributes as being useless, as when their values exhibit no significantly different distributions for different sets--if not, we replace r by the number of useful attributes.) Hence we need
bits.
Level 3: we need twice as much space as level 2 to include the second highest frequency and the median frequency statistics too, hence
bits.
Level 4: we can describe a distribution either implicitly (by a mathematical formula approximating it) or explicitly (by listing of values). For implicit storage, we need to specify a distribution function and absolute deviations above and below it (since the original distribution is discrete, it is usually easier to use the corresponding cumulative distributions). We can use codes for common distributions (like the uniform distribution, the exponential, and the Poisson), and we need a few distribution parameters of w bits, plus the positive and negative deviation extrema of w bits each too. So space will be similar to level 3 information.
If a distribution is not similar to any known distribution, we must represent it explicitly. Assume data items are aggregated into approximately equal-size groups of values; the m-fold partitioning that defined the original sets is probably good (else we would not have chosen it for the other purpose originally), so let us assume it. Then we have a total of
. If some of the groups of values (bins) on a set are zero, we can of course omit them and save space.
Level 5: this information is similar to level 4 except that values are associated with points of the distribution. Implicit representation by good-fit curves requires just as much space as level-4 implicit representation--we just impose a fixed ordering of values along the horizontal axis instead of sorting by frequency. Explicit representation also takes the level 4 of
We also need storage for access structures. If users query only a few named
sets, we can just store the names in a separate lexicon table mapping names to
unique integer identifiers, requiring a total of 
bits for the table, where l is the
average length of a name, assuming all statistics on the same set are stored
together.
But if users want to query arbitrary value partitions of attributes, rather
than about named sets, we must also store definitions of the sets about which
we have tabulated statistics. For sets that are partitions of numeric
attributes, the upper and lower limits of the subrange are sufficient, for 2mw
bits each. But nonnumeric attributes are more trouble, because we usually have
no alternative than to list the set to which each attribute value belongs. We
can do this with a hash table on value, for 
bits assuming a 50% hash table
occupancy. Thus total storage is approximately 
.
A variety of compression techniques can be applied to storage of statistics, extending standard compression techniques for databases [15]. Thus the storage calculations above can be considered upper bounds.
These storage requirements are not necessarily bad, not even the level 4 and 5 explicit distributions. In many databases, storage is cheap. If a set intersection is often used, or a bound is needed to determine how to perform a large join when a wrong choice may mean hours or days more time, quick reasoning with a few page fetches of precomputed statistics (it's easy to group related precomputed statistics on the same page) will usually be much faster than computing the actual statistic or estimating it by unbiased sampling. That is because the number of page fetches is by far the major determinant of execution time for this kind of simple processing. Computing the actual statistic would require looking at every page containing items of the set; random sampling will require examining nearly as many pages, even if the sampling ratio is small, because except in the rare event in which the placement of records on pages is random (generally a poor database design strategy), records selected will tend to be the only records used on a page, and thus most of the page-fetch effort is "wasted." Reference [14] discusses these issues further.
5. Evaluation of the frequency-distribution bounds
5.1 Comparing bounds
We can prove some relationships between frequency-distribution bounds on
intersections (see Figure 2):
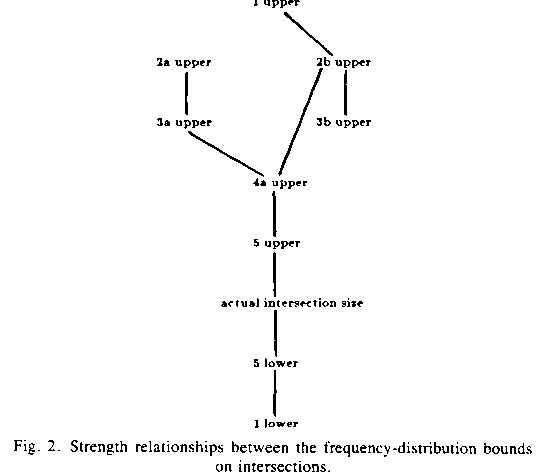
1. Level 2b upper bounds are better than level 1 since
2. Level 3a upper bounds are better than level 2a because you get the latter if you substitute m(i,j) for m2(i,j) and mf(i,j) in the former, and
and
.
3. Level 3b upper bounds are better than level 2b because
4. Level 4a upper bounds are better than level 3a because the mode frequency is an upper bound on the frequency of the half of the most frequent values, and the median frequency is an upper bound on the frequency of the other half. Hence writing the level 3a expression in brackets as a summation of d(U,j) terms comparable to that in the level 4a summation, each level-3a term is an upper bound on a corresponding level-4 term.
5. Level 4a upper bounds are better than level 2b since they represent repeated application of level-2b bounds to subsets of the sets intersected.
6. Level 5 upper bounds are better than level 4a by the proof in Appendix B.
7. Level 5 lower bounds are better than level 1 lower bounds because level 5 partitions the level 1 sets into many subsets and computes lower bounds separately on each subset instead of all at once.
Analogous arguments hold for bounds on unions since rules for unions were created from rules for intersections.
5.2 Experiments
There are two rough guidelines for bounds on set intersection and union sizes to be more useful than estimates of those same things:
1. Some of the sets being intersected or unioned are significantly nonindependent (that is, not drawn randomly from some much larger population). Hence the usual estimates of their intersection size obtained from level 1 (size of the intersected sets) information will be poor.
2. At least one set being intersected or unioned has a significantly different frequency distribution from the others on at least one attribute. This requires that at least one set has values on an attribute that are not randomly drawn.
These criteria can be justified by the general homomorphism idea behind our approach (see section 3): good bounds result whenever values in the range of the homomorphism get very different counts mapped onto them for each set considered. These criteria can be used to decide which sets on a database it might be useful to store statistics for computing bounds.
5.2.1 Experiments: nonrandom sets
As a simple illustration, consider the experiments summarized in the tables
of Figures 3 and 4. We created a synthetic database of 300 tuples of four
attributes whose values were evenly distributed random digits 0-9. We wrote a
routine (MIX) to generate random subsets of the data set satisfying the above
two criteria, finding groups of subsets that had unusually many common values.
We conducted 10 experiments each on random subsets of sizes 270, 180, 120, and
30. There were four parts to the experiment, each summarized in a separate
table. In the top tables in Figures 3 and 4, we estimated the size of the
intersection of two sets; in the lower tables, we estimated the size of the
intersection of four sets. In Figure 3 the chosen sets had 95% of the same
values; in Figure 4, 67%.
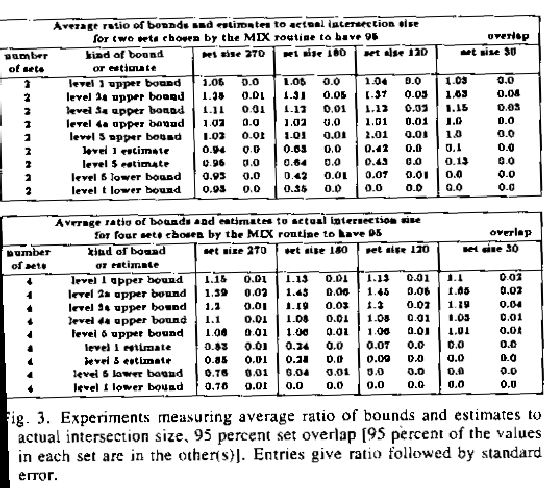
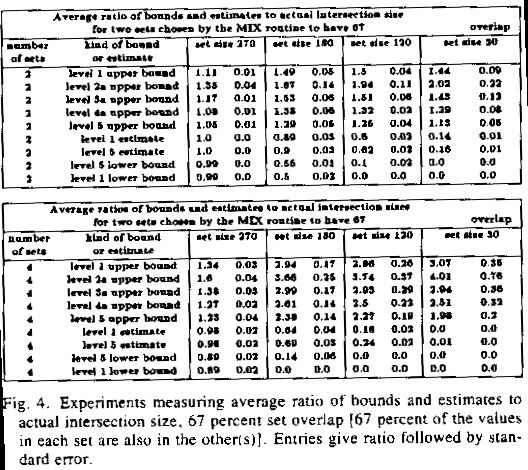
The entries in the tables represent means and standard deviations in 10 experiments of the ratios of bounds or estimates to the actual intersection size. There are four pairs of columns for the four different set sizes investigated. The rows correspond to the various frequency-distribution levels discussed: the five levels of upper bounds first, then two estimate methods, then the two lower bound methods. (Since level 5 information is just level 1 information at a finer level of detail, it is easier to generalize the level 1 estimate formula to a level 5 estimate formula.) Only level 2a and 3a rules were used, not 2b and 3b.
The advantage of bounds shows in both Figure 3 and Figure 4, but more dramatically in Figure 3 where sets have the 95% overlap. Unsurprisingly, lower bounds are most helpful for the large set sizes (left columns), whereas upper bounds are most helpful for the small set sizes (right columns). However, the lower bounds are not as useful because when they are close to the true set size (i.e. the ratio is near 1), estimates are also close. But when upper bounds are close to the true set size for small sets, both estimates and lower bounds can be far away.
5.2.2 Experiments: real data
The above experiments were with synthetic data, but we found similar phenomena with real-world data. A variety of experiments, summarized in [17], were done with data extracted from a database of medical (rheumatology) patient records. Performance of estimate methods vs. our bounding methods was studied for different attributes, different levels of information, and different granularities of statistical summarization. Results were consistent with the preceding ones for a variety of set types. This should not be surprising since our two criteria given previously are often fulfilled with medical data, where different measures (tests, observations, etc.) of the sickness of a patient often tend to correlate.
6. Bounds from range analysis
Frequency-distribution bounds are only one example of a class of bounding methods involving mappings (homomorphisms) of a set of data items onto a distribution. Another very important example are bounds obtained from analysis on the range of values for some attribute, call it j, of the data items for each set intersected. These methods essentially create new sets, defined as partitions on j, which contain the intersection or union being studied. These new sets can therefore can be included in the list of sets being intersected or unioned without affecting the result, and this can lead to tighter (better) bounds on the size of the result. Many formulas analogous to those of section 4 can be derived.
6.1 Intersections on univariate ranges
6.1.1 Statistics on partitions of an attribute
All the methods we will discuss require partition counts on some attribute j. That is, the number of data items lying in mutually exclusive and exhaustive ranges of possible values for j. For instance, we may know the number of people ages 0-9, 10-19, 20-29, etc.; or the number of people with incomes 0-9999, 10000-19999, 20000-29999, etc. We require that the attribute be sortable by something other than item frequency in order for this partitioning to make sense and be different from the frequency-distribution analysis just discussed; this means that most suitable attributes are numeric.
This should not be interpreted, however, as requiring anticipation of every partition of an attribute that a user might mention in a query, just a covering set. To get counts on arbitrary subsets of the ranges, inequalities of the Chebyshev type may be used when moments are known, as for instance Cantelli's inequalities:
[probability that
]
for μ the mean and σ the standard deviation of the attribute. Otherwise the count of a containing range partition may be used as an upper bound on the subset count.
6.1.2 Upper bounds from set ranges and bin counts on the universe (level 1)
Suppose we know partition (bin) counts on some numeric attribute j for the universe U. (We must know them for at least one set to apply these methods, so it might as well be the universe.) Suppose we know the maximum h(i,j) and minimum l(i,j) on attribute j for each set i being intersected. Then an upper bound on the maximum of the intersection H(j), and a lower bound on the minimum of the intersection L(j) are
Note if H(j)<L(j) we can immediately say the intersection is the empty set. Similarly, for the union of sets
So an intersection or union must be a subset of U that has values bounded by L(j) and H(j) on attribute j, for any numeric attribute j. So an upper bound on the size of an intersection or union is the minimum-size such range-partition set over all attributes j in Q, or
where s sets are intersected; where there are r numeric attributes; where B(x,j) denotes the number of the bin into which value x falls on attribute j; and where binfreq(U,j,k) is the number of items in partition (bin) k on attribute j for the universe U.
Absolute bounds on correlations between attributes may also be exploited. If two numeric attributes have a strong relationship to each other, we can formally characterize a mapping from one to the other with three items of information: the algebraic formula, an upper deviation from the fit to that formula for the universe U, and a lower deviation. We can calculate these three things for pairs of numeric attributes on U, and store only the information for pairs with strong correlations. To use correlations in finding upper bounds, for every attribute j we find L(j) and H(j) by the old method. Then, for every stored correlation from an arbitrary attribute j1 to an arbitrary attribute j2, we calculate the projection of the range of j1 (from L(j1) to H(j1)) by the formula onto j2. The overlap of this range on the original range of j2 (from L(j2) to H(j2)) is then the new range on j2, and L(j2) and H(j2) are updated if necessary. Applying these correlations requires iterative relaxation methods since narrowing of the range of one attribute may allow new and tighter narrowings of ranges of attributes to which that attribute correlates, and so on.
6.1.3 Upper bounds from mode frequencies on bin counts for intersected sets (level 2)
At the next level of information, analogous to level 2 for frequency-distribution bounds, we can have information about distributions of values for particular sets. Suppose this includes an upper bound m(i,j) on the number of things in set i in a bin of some attribute j. (This m(i,j) is like the mode frequency in section 4, except the equivalence classes here are all items in a certain range on a certain attribute.) Assume as before we know what bins a given range of an attribute covers. Then an upper bound on the size of the set intersection is
where H(j) and L(j) are as before. Similarly, an upper bound on the size of a set union is
6.1.4 Upper bounds from bin counts for intersected sets (level 5)
Finally, if we know the actual distribution of bin counts for each set i being intersected, we can modify the intersection formula of level 1 as follows:
where s sets are intersected; where there are r numeric attributes; where B(x,j) is the number of the bin into which value x falls on attribute j; and where binfreq(i,j,k) is the number of items in partition (bin) k on attribute j for set i. Similarly, the union upper bound is:
As with frequency-distribution level 4a and level 5 bounds, we can also use this formula when all we know is an upper bound on the bin counts, perhaps from a distribution fit.
6.2 Multidimensional intersection range analysis
Analogous to range analysis, we may be able to obtain a multivariate distribution that is an upper bound on the distribution of the data universe U over some set S of interest (as discussed in [9] and [2]). We determine ranges on each attribute of S by finding the overlap of the ranges for each set being intersected as before. This defines a hyperrectangular region in hyperspace, and the universe upper bound also bounds the number of items inside it. We can also use various multivariate generalizations of Chebyshev's inequality [1] to bound the number of items in the region from knowledge of moments of any set containing the intersection set (including the universe). As with univariate range analysis, we can exploit known correlations to further truncate the ranges on each attribute of S, obtaining a smaller hyperrectangular region.
Another class of correlation we can use is specific to multivariate ranges: those between attributes in the set S itself. For instance, a tight linear correlation between two numeric attributes j1 and j2, strongly limits the number of items within rectangles the regression line does not pass through. If we know absolute bounds on the regression fit we can infer zero items within whole subregions. If we know a standard error on the regression fit we can use Chebyshev's inequality and its relatives to bound how many items can lie certain distances from the regression line.
Just as for univariate range analysis, we can exploit more detailed information about the distributions of any attribute (not necessarily the ones in S). If we know an upper bound on bin size, for some partitioning into subregions or "bins", or if we know the exact distribution of bin sizes, we may be able to improve on the level 1 bounds.
6.3 Lower bounds from range analysis
Lower bounds can be obtained from substituting the above upper bounds in the first three formulae relating intersections and unions in section 4.4.1, either substituting for the intersection or for the union. Unfortunately the resulting formulae are complicated, so we won't give them here.
6.4 Embedded set expressions for range analysis
Let us consider the effect of Boolean equivalences on embedded set descriptions for the above range-analysis bounds, for level 1 information. First, range-analysis bounds cannot be provided for expressions with set complements in them, because there is no good way to determine a maximum or minimum of the complement of a set other than the maximum or minimum of the universe. So none of the equivalences involving complements apply.
The only set-dependent information in the level-1 calculation are the
extrema of the range, H and L. Equivalence of set expressions under
commutativity or associativity of terms in intersections or unions then follows
from the commutativity of the maxima and minima of operations, as does
distributivity of intersections over unions and vice versa. Equivalence under
reflexivity follows because max(a,a) = a and min(a,a) = a. Introduction of
terms for the universe and the null set are useless, because the max(a,0) = a
for 
,
and min(a,N) = a. So expression rearrangements do not affect the bounds, so we
might as well not bother; that seems a useful heuristic for level 2 and 5
information too.
6.5 Storage requirements for range analysis
Space requirements for these range analysis bounds can be computed in the same way as for the frequency-distribution bounds. Assume that the number of bins on each attribute is m, the average number of attributes is r, the number of bits required for each attribute value is w, and the number of items in the database is N. Then the space requirements for univariate range bounds are:
Again, these are pessimistic estimates since they assume that all attributes can be helpful for range analysis.
6.6 Evaluation of the range-analysis bounds
Level 2 upper bounds are definitely better than level 1 because the binfreq(U,j,k) is an upper bound on mf(i,j); level 5 is better than level 2 because mf(i,j) is an upper bound on binfreq(i,j,k). But the average-case performance of the range-analysis bounds is harder to predict than that of the frequency-distribution bounds, since the former depends on widely-different data distributions, while the latter's distributions tend to be more similar. Furthermore, maxima and minima statistics have high variance for randomly distributed data, so it is hard to create an average-case situation for them; strong range-restriction effects do occur with real databases, but mostly with human-artifact data that does not fit well to classical distributions. Thus no useful average-case generalizations are possible about range-analysis bounds.
6.7 Cascading range-analysis and frequency-distribution methods
The above determination of the maximum and minimum of an intersection set on an attribute can be used to find better frequency-distribution bounds too, since it effectively adds new sets to the list of sets being intersected, sets defined as partitions of the values of particular attributes. These new sets may have unusual distributions on further attributes that can lead to tight frequency-distribution bounds.
7. Conclusion
We have provided a library of formulae for bounds on the sizes of intersections, unions, and complements of sets. We have emphasized intersections (because of their greater importance) and intersection upper bounds (because they are easier to obtain). Our methods exploit simple precomputed statistics (counts, frequencies, maxima and minima, and distribution fits) on sets. The more we precompute, the better our bounds can be. We illustrated by analysis and experiments the time-space-accuracy tradeoffs involved between different bounds. Our bounds tend to be most useful when there are strong or complex correlations between sets in an intersection or union, a situation in which estimation methods for set size tend to do poorly. This work thus nicely complements those methods.
References
Author's address: Neil C. Rowe, Department of Computer Science, Code 52Rp, Naval Postgraduate School, Monterey, CA 93943 USA.
Acknowledgements: The work reported herein was partially supported by the Foundation Research Program of the Naval Postgraduate School with funds provided by the Chief of Naval Research. The views and conclusions contained in this document are those of the author and should not be interpreted as representative of the official policies of the U. S. Navy or the U. S. Government. Barry Tilden provided helpful discussion. Judy Quesenberry and Helen Guyton helped with typing. Reviewers provided many valuable comments.
[1] H. W. Block and A. R. Sampson, "Inequalities on distributions: bivariate and multivariate," in The Encyclopedia of Statistical Sciences, volume 4. New York: Wiley, 1983, 76-82.
[2] S. Christodoulakis, "Estimating record selectivities," Information Systems, 8, 2, 105-115, 1983.
[3] L. H. Cox, "Suppression methodology and statistical disclosure control," Journal of the American Statistical Association, 75, 370, 377-385, June 1980.
[4] R. Demolombe, "Estimation of the number of tuples satisfying a query expressed in predicate calculus language," Proceedings of the Sixth Conference on Very Large Data Bases, September 1980, 55-63.
[5] D. E. Denning and J. Schlorer, "Inference controls for statistical databases," IEEE Computer, 16, 7, 69-81, July 1983.
[6] E. L. Lawler, "An approach to multilevel boolean minimization," Journal of the ACM, 11, 3, 283-295, July 1964.
[7] E. Lefons, A. Silvestri, and F. Tangorra, "An analytic approach to statistical databases," Proceedings of the Ninth International Conference on Very Large Data Bases, Florence, Italy, September 1983, 260-274.
[8] W. Lipski, "On semantic issues connected with incomplete information databases," ACM Transaction on Database Systems, 4, 3, 262-296, September 1979.
[9] T. Merett and E. Otoo, "Distribution models of relations," Proceedings of the Fifth International Conference on Very Large Data Bases, Rio de Janeiro, Brazil, 1979, 418-425.
[10] G. Piatetsky-Shapiro and C. Connell, "Accurate estimation of the number of tuples satisfying a condition," Proceedings of the ACM-SIGMOD Annual Meeting, Boston, Mass., June 1984, 256-276.
[11] P. Richard, "Evaluation of the size of a query expressed in relational algebra," Proceedings of the ACM-SIGMOD Annual Meeting, June 1981, 155-163.
[12] N. C. Rowe, "Rule-based statistical calculation on a database abstract," Report STAN-CS-83-975, Stanford University Computer Science Department, June 1983 (Ph. D. thesis).
[13] N. C. Rowe, "Diophantine inferences on a statistical database," Information Processing Letters, 18, 25-31, 1984.
[14] N. C. Rowe, "Antisampling for estimation: an overview," IEEE Transactions on Software Engineering, SE-11, 10, 1081-1091, October 1985.
[15] D. Severance, "A practitioner's guide to data base compression," Information Systems, 8, 1, 51-62, 1983.
[16] A. Shoshani, "Statistical databases: characteristics, problems, and some solutions," Proceedings of the 8th International Conference on Very Large Data Bases, Mexico City, Mexico, 1982, 208-222.
[17] B. M. Tilden, "A hierarchy of knowledge levels implemented in a rule-based production system to calculate bounds on the size of intersection and unions of simple sets," M. S. Thesis, U. S. Naval Postgraduate School, December 1984.
[18] J. D. Tukey, Exploratory Data Analysis. Reading, Mass.: Addison-Wesley, 1977.
Appendix A: Best equivalent forms for level 1 frequency-distribution bounds
We give here the detailed comparison of level 1 frequency-distribution bounds (both upper and lower) for set expressions equivalent under Boolean algebra.
A.1 Commutativity
The order of sets in an intersection or union does not matter because examination of the rules shows this only changes the order of a sum, minimum, or maximum, and those operations are commutative.
A.2 Reflexivity
Since
the equivalent expression of just the set A is preferable for obtaining bounds.
A.3 Associativity of intersection
Let 
where
. (By
embedding these groupings, we can model an arbitrary associative computation
scheme.) Then the upper bounds are equivalent since the minimum operator is
associative. The lower bounds are also equivalent:
We have three cases to consider for each of the inner max expressions for Q2:
(1) Suppose the second argument of both is the larger; then the expression for Q2 becomes that for Q1.
(2) Second, suppose the first inner max expression is zero. (This includes the case where the second inner max is zero too.) Since
the outer max must be zero. So the Q2 lower bound is zero. But since
and the first term in brackets is less than 0, and the second term in brackets is less than or equal to N, the right side must be less than 0. Hence the Q1 lower bound is zero too.
(3) Third, suppose the second inner max in the Q2 bound is zero. Then the Q1 and Q2 bounds are equal.
A.4 Associativity of union
From the last section it follows that associativity does not matter to set unions, because any union of s sets can be written as the complement of the intersection of the complements of those sets, and there is no additional uncertainty introduced in the handling of complements of sets (just subtract the size or the bound from N).
A.5 Distributivity of intersection over union
The distributive law of intersection over union does not preserve level-1 bounds: the factored form is preferable. Let
Then:
Case 1: 
for some i. Then a = min(a,b(i))
for some i, and since a and b(i) are always nonnegative, 
.
Case 2: b(i)<a for all i. Then b(i) = min(a,b(i)) and 
. Hence in
both cases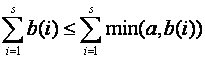 
and 
and so the upper bound on Q3 (the "factored out" form) is always less than or equal to the upper bound on Q4, and hence preferable.
The lower bounds on Q3 and Q4 are:
which are equivalent since the latter represents a valid scope extension of the second max in the former.
A.6 Distributivity of union over intersection
Similar analysis shows that the factored form for distribution of union over intersection is also preferable.
A.7 The universal set, the null set, and absorption
Let U represent the universe and 
the empty set. Then:
So it does not matter to the bounds which we take. For the "absorption" laws
the latter forms are obviously preferable.
A.8 Negation equivalences
We have not yet considered negation, but it causes few difficulties. First
note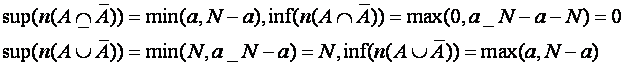 
so it is better to replace 
with U, and 
with . We can use this to show
another form of absorption is desirable:
DeMorgan's Laws always give two equivalent expressions:
Appendix B: proof of the superiority of level 5 frequency-distribution upper bounds to level 4a
For any attribute j, level 5 and level 4a upper-bound calculation can be expressed as operating on a matrix in which the entry in row i and column k represents the kth frequency for set i; this matrix has s rows and d(U,j) columns. But level 4a rows are sorted by decreasing values while level 5 rows are not. To show that level 5 bounds are superior (less than or equal to) level 4a bounds, we show that the level 4a matrix can be created by a series of binary interchanges on the level 5 matrix, where each interchange cannot improve the criterion for the matrix, the summation of the minima of the columns.
First we prove this for a two-row matrix. Suppose we first sort the columns
by decreasing order of second-row frequencies. Now consider sorting the
first-row frequencies by a d(U,j)-step process. For each step k, we pick the
largest element in the first row exclusive of the first k-1 items, and
interchange it with the element in column k. Suppose at some step we
interchange a currently-largest value a with another value b, and suppose value
a is originally in the same column with d in the second row, and b is
originally in the same column with c in the second row. The only effect of this
interchange is to substitute in the criterion an expression min(a,c)+min(b,d)
for an expression min(a,d)+min(b,c), and assume and 
. We can verify the first
expression is an upper bound on the second by considering the six cases in turn
(see Figure 5). Thus the level-4 upper bound is itself an upper bound on the
level-5 upper bound.
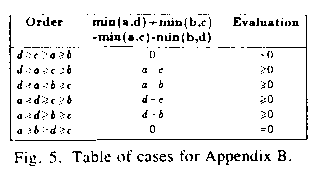
The result for a two-row matrix easily extends to matrices with more rows, if we just replace references to the values in the second row in the above by references to the minimum value in the column for all but the first-row value. Thus the general result is proved.
Captions for Figures
Figure 1: Table of Boolean-equivalence effects on bounds
Figure 2: Strength relationships between the frequency-distribution bounds on intersections
Figure 3: Experiments measuring average ratio of bounds and estimates to actual intersection size, 95% set overlap (95% of the values in each set are in the other(s)). Entries give ratio followed by standard error.
Figure 4: Experiments measuring average ratio of bounds and estimates to actual intersection size, 67% set overlap (67% of the values in each set are also in the other(s)). Entries give ratio followed by standard error.
Figure 5: Table of cases for Appendix B