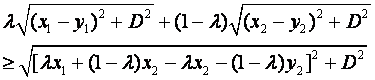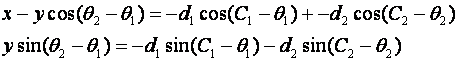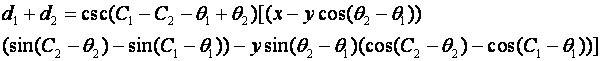Optimal grid-free path planning across arbitrarily-contoured terrain with anisotropic friction and gravity effects
Neil C. Rowe and Ron S. Ross
Department of Computer Science
Code 52Rp, Naval Postgraduate School Monterey, CA 93943
Abstract
Anisotropic (heading-dependent) phenomena arise in the "two-and-one-half-dimensional" path-planning problem of finding minimum-energy routes for a mobile agent across some hilly terrain. We address anisotropic friction and gravity effects, and ranges of impermissible-traversal headings due to overturn danger or power limitations. Our method does not require imposition of a uniform grid, nor average effects in different directions, but reasons about a polyhedral approximation of terrain. It reduces the problem to a finite but provably-optimal set of possibilities, and then uses A* search to find the cost-optimal path. However, the possibilities are not physical locations but path subspaces. Our method exploits the surprising insight that there are only four ways, mathematically simple, to optimally traverse an anisotropic homogeneous region: (1) straight across without braking, the standard isotropic-weighted-region traversal; (2) straight across without braking but as close as possible to a desired impermissible heading; (3) making impermissibility-avoiding switchbacks on the path across a region; and (4) straight across with braking. We prove specific optimality criteria for transitions on the boundaries of regions for each combination of traversal types. These criteria subsume previously published criteria for traversal of isotropic weighted-region terrain. Our method can take considerably less computer time and space than previous methods on some terrain; at the same time, we believe it is the first algorithm to provide truly optimal paths on anisotropic terrain.
This work was supported in part by the U. S. Army Combat Developments Experimentation Center under MIPR ATEC 88-86. Special thanks to Yutaka Kanayama and Robert McGhee. This paper appeared in IEEE Transactions on Robotics and Automation, 6, no. 5 (October 1990), 540-553. The equations were redrawn in 2008.
Introduction
We consider the problem of mobile-agent optimal-path planning between some start point and some goal point on terrain with arbitrary contours, using a simple physical model with gravity and friction forces. We address only "high-level" path planning, as for instance outdoors to a resolution of 100 meters or so, for which (1) the agent traversing the path is much smaller than path dimensions, and (2) terrain elevation and rough surface-covering information is available. We treat this as a two-dimensional problem in which we reason in the projection of the surface onto a two-dimensional map plane perpendicular to the direction of gravity. We assume we wish to minimize either energy cost or, when power is constant, traversal time (since then work is power times time). We allow that in certain regions of the terrain (whose boundaries will be defined by polygons), certain directions of travel are impermissible (of infinite cost).
Furthermore, we want a grid-free solution method, one that does not impose a feature-independent grid on the terrain and try to figure how a wavefront would propagate across this grid [9, 3], but tries to reason about terrain features like hills and ridges, only partitioning terrain as absolutely necessary. Grid-based methods are versatile, and preferable to the methods we propose here for a variety of applications, as on very heterogeneous terrain. But they can have several serious disadvantages: (1) potentially much wasted computation, since search for the goal is mostly blind; (2) potentially much wasted space, since homogeneous areas of the terrain require as much storage per unit area as heterogeneous areas; (3) directional biases in the propagation grid giving path-cost errors; (4) accumulation of roundoff errors; (5) digitalization effects causing unreasonable jagged paths where the optimal path should be straight (while jagged paths can be smoothed, there are many kinds of smoothing to choose among, and optimality or even feasibility of the smoothed path cannot be guaranteed); and (6) inability to converge to the optimal solution as grid size increases. [15, 6] discuss these disadvantages in more detail for a related problem. Note that disadvantage (4) is particularly serious for grid algorithms on anisotropic terrain, because repeated rounding to the same side of the recommended path direction, as in near-homogeneous terrain, will force the path further and further afield; on the other hand, increasing the number of angles of propagation effectively decreases the resolution of the grid quickly. Because of this, grid-propagation algorithms cannot provide guaranteed-optimal paths on anisotropic terrain.
Our previous work [15, 14, 12] and that of [8] successfully explored grid-free methods for regions of different internally-homogeneous cost per traversal distance, but assuming isotropism (no effect of travel direction on cost). These techniques can give guaranteed-optimal paths. We extend these approaches in this paper to the most important kinds of anisotropism that arise in overland path planning.
The physical model
The basic energy-cost model
We study minimum-energy paths for an agent (perhaps a mobile robot or army
vehicle) moving across some hilly terrain in only a forward direction. (This
problem should not be confused with the "geodesic" problem of finding
the path that minimizes the surface-travel distance between two points [7].)
Assuming that the agent has no net acceleration over the path, and that path
turns altogether involve insignificant energy loss, the major external forces
operating on the agent are gravity and friction [1, 16]. Then when the agent is
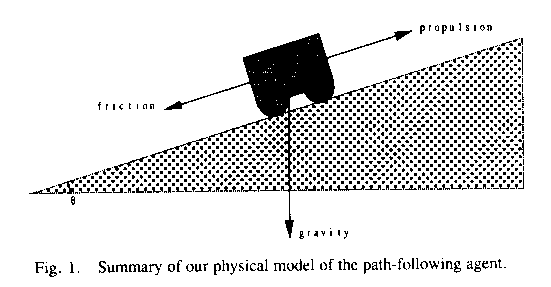
traversing a slope of ![]() (positive uphill, negative
downhill) in the direction of the gradient (see Figure 1), the sum of the two
forces is
(positive uphill, negative
downhill) in the direction of the gradient (see Figure 1), the sum of the two
forces is ![]() using
the classic model from physics of a body on an inclined plane, where mg is
agent weight and
using
the classic model from physics of a body on an inclined plane, where mg is
agent weight and ![]() is the coefficient of friction
or specific resistance that is working against the vehicle. (This is derived
from a more complex model in [13]). This is the external work per unit of
surface distance that must be expended by the vehicle to overcome nature, so
the energy cost of a path is its integral over the path. (This formula was
confirmed experimentally within 1% for wheeled vehicles on slopes of less than
20% in [16], with
is the coefficient of friction
or specific resistance that is working against the vehicle. (This is derived
from a more complex model in [13]). This is the external work per unit of
surface distance that must be expended by the vehicle to overcome nature, so
the energy cost of a path is its integral over the path. (This formula was
confirmed experimentally within 1% for wheeled vehicles on slopes of less than
20% in [16], with ![]() interpreted as the ratio of
drawbar pull to vehicle weight.)
interpreted as the ratio of
drawbar pull to vehicle weight.)
However, we must make two changes to the formula to make it general. First,
if we are not traveling straight uphill or straight downhill, the normal force
is not coplanar with the plane of Figure 1, and depends only on the gradient.
Letting ![]() be
the inclination angle of the gradient, the sum of the two forces becomes
be
the inclination angle of the gradient, the sum of the two forces becomes ![]() . Second, we can
modify this formula to reason about paths in their two-dimensional azimuth
projections onto a map plane, and thereby turn path planning into a
two-dimensional problem. The perceived length of a path on a slope viewed from
directly above is the actual length times the cosine of the slope angle. Then
the cost per unit of perceived distance is
. Second, we can
modify this formula to reason about paths in their two-dimensional azimuth
projections onto a map plane, and thereby turn path planning into a
two-dimensional problem. The perceived length of a path on a slope viewed from
directly above is the actual length times the cosine of the slope angle. Then
the cost per unit of perceived distance is ![]() . Because
. Because ![]() and
and ![]() is very
close to 1 for most traversable natural terrain,
is very
close to 1 for most traversable natural terrain, ![]() is very close to 1, and we will
generally ignore it subsequently. Then the energy lost to friction depends only
on the length of the path as viewed from above. Furthermore, the work expended
against gravity is just the sum over all path segments of the perceived
distance times the tangent of the slope for each path segment, or the sum of
all the elevation changes; so the total work against gravity is independent of
the path between two points, and can be ignored in finding the optimal path.
Hence only distance and the coefficient of friction are significant in finding
minimum-energy nonbraking paths.
is very close to 1, and we will
generally ignore it subsequently. Then the energy lost to friction depends only
on the length of the path as viewed from above. Furthermore, the work expended
against gravity is just the sum over all path segments of the perceived
distance times the tangent of the slope for each path segment, or the sum of
all the elevation changes; so the total work against gravity is independent of
the path between two points, and can be ignored in finding the optimal path.
Hence only distance and the coefficient of friction are significant in finding
minimum-energy nonbraking paths.
To facilitate mathematical analysis, we assume as in the Army Mobility Model [18] and our own earlier work based on it [12, 15] that the terrain is partitioned into polygonal regions within which the coefficient of friction can be assumed constant; any terrain can be sufficiently closely approximated by some such polygons [10]. For overland terrain, often this can be done from map overlays or classification of surface covering in aerial photography.
Internal energy losses in the agent are often proportional to external work done against gravity and friction (as the heat losses in an engine), multiplying the cost by a constant that can be ignored. Other such losses can be modeled as proportional to path distance (as the friction of wheels on an axle, and wind resistance when the wind is constant-speed parallel to the surface), so the minimum-distance path will minimize these too. The optimal paths in this paper require turns which do add extra energy cost, but it is usually negligible compared to the overall path cost, so we will call it a "second-order" cost. Specifically, if two paths have the same energy or "first-order" cost, the one with the fewest turns is preferred.
Anisotropic phenomena with braking
When the above cost formula becomes negative, the agent is gaining energy in going downhill. This would cause an agent to accelerate, and since there are limits to safe acceleration and safe speed of an agent, we assume braking must occur sufficient to give no net acceleration on any downhill path segment. Braking causes energy loss as heat, energy which cannot be recovered.
For braking-phenomena analysis, we will need reasonably detailed information about surface elevation, like the grid of elevation readings given in Defense Mapping Agency data. Such data can be fitted to an irregular polyhedron by least-squares fitting of planar patches (see Section 6). The projections of polyhedral faces to the two-dimensional map plane define boundaries of constant-gradient regions. These can be further subdivided by intersecting them with the constant-friction regions mentioned earlier, to give subregions with both constant gradient and constant coefficient of friction.
For a polyhedral-face region with gradient inclination (steepness angle) ![]() and gradient
azimuth (direction in the map plane)
and gradient
azimuth (direction in the map plane) ![]() , it follows by geometry that the
vehicle inclination
, it follows by geometry that the
vehicle inclination ![]() at the azimuth
at the azimuth ![]() is
is ![]() . For a
particular direction of travel
. For a
particular direction of travel ![]() we can compare this with the
"critical braking slope" at which braking starts; braking only occurs
for downward inclinations more than this. The two symmetric azimuth directions
corresponding to this critical slope we will call the "critical braking
headings"; together they delimit the "braking range".
we can compare this with the
"critical braking slope" at which braking starts; braking only occurs
for downward inclinations more than this. The two symmetric azimuth directions
corresponding to this critical slope we will call the "critical braking
headings"; together they delimit the "braking range".
Braking requires negligible energy. However, if we use map distance as the
cost for nonbraking traversal, we must assign a "virtual cost" to
braking episodes to be consistent; braking increases the cost per distance
predicted by the formula to zero from the negative number of ![]() , so the virtual
cost is the negative of this. This is equivalent to replacement of a friction
cost
, so the virtual
cost is the negative of this. This is equivalent to replacement of a friction
cost ![]() for
the segment by
for
the segment by ![]() .
This is always positive since braking always occurs downhill, when
.
This is always positive since braking always occurs downhill, when ![]() is negative.
This change in cost formula must occur at the azimuth angles defined by
is negative.
This change in cost formula must occur at the azimuth angles defined by ![]() , or when the
inclination angle is
, or when the
inclination angle is ![]() . Hence the virtual cost of a
traversal of distance D is (1)
. Hence the virtual cost of a
traversal of distance D is (1) ![]() for nonbraking traversal, and
(2)
for nonbraking traversal, and
(2) ![]() , or
the elevation difference, for braking traversal.
, or
the elevation difference, for braking traversal.
Lemma 2.1: The cost formula value for nonbraking traversal ![]() compares
to the cost formula value for braking traversal
compares
to the cost formula value for braking traversal ![]() (
( ![]() the first elevation,
the first elevation, ![]() the
second) in the following way: (1) for a downhill braking slope, the second
value is larger; (2) for a critical braking slope downhill, the two values are
equal; (3) for any other slope (nonbraking), the first value is larger.
Proof: from the discussion in Section 2, case (1) means
the
second) in the following way: (1) for a downhill braking slope, the second
value is larger; (2) for a critical braking slope downhill, the two values are
equal; (3) for any other slope (nonbraking), the first value is larger.
Proof: from the discussion in Section 2, case (1) means ![]() , (2) means
, (2) means ![]() , and (3) means
, and (3) means ![]() . By rearranging
the inequalities and equation, and observing
. By rearranging
the inequalities and equation, and observing ![]() , the results follow.
, the results follow.
Error analysis of the cost calculations
For the outdoor paths that are our primary application interest, Defense
Mapping Agency information is quite detailed for the high-level planning we are
concerned with. So for these paths, the major source of error in our cost
computations will be variation in the coefficient of friction ![]() within
regions. These variations will tend to average out for long traversals and be
negligible. Errors also arise in the polyhedral fit. This has an effect on
heading ranges of permissible traverse, for which the cost error is hard to
predict, and in the cost of braking episodes, for which the cost error is the
cumulative elevation error and hence is small.
within
regions. These variations will tend to average out for long traversals and be
negligible. Errors also arise in the polyhedral fit. This has an effect on
heading ranges of permissible traverse, for which the cost error is hard to
predict, and in the cost of braking episodes, for which the cost error is the
cumulative elevation error and hence is small.
Time-minimizing paths
The nonbraking path that minimizes energy consumption between a start point
and a goal point is also the minimum-time nonbraking path under constant power
consumption, assuming power is sufficient for all uphill slopes. This is
because the velocity and all forces acting against the agent are parallel to
the surface, so work is Pt, P the power and t the time. During braking
episodes, a time-minimizing agent can travel as fast as is comfortable, call it
![]() . It is
straightforward to define a "virtual time cost" for braking episodes
equal to
. It is
straightforward to define a "virtual time cost" for braking episodes
equal to ![]() ,
which has an extra term representing the nonzero actual time required. Note
that the extra term depends on path length, so the turn
"second-order" path cost referred to in energy-minizing paths is even
more important for time-minimizing paths.
,
which has an extra term representing the nonzero actual time required. Note
that the extra term depends on path length, so the turn
"second-order" path cost referred to in energy-minizing paths is even
more important for time-minimizing paths.
Anisotropic-obstacle phenomena
Anisotropism also arises with "anisotropic obstacles", regions sufficiently steep to absolutely rule out certain directions of travel. Such regions have pairs of "critical impermissibility headings", permissible headings delimiting a range of impermissible azimuth directions for traversal. Again, a polyhedral terrain fit greatly simplifies analysis because these ranges will be the same everywhere on a polyhedral facet.
[16] indicates four conditions can give anisotropic slope limitations.
First, an agent may be limited in force expenditure in trying to counteract
gravity and friction; call this ![]() . For our simple physics model, this
means the slope angle cannot exceed
. For our simple physics model, this
means the slope angle cannot exceed ![]() . (This was experimentally confirmed
within 2% for wheeled vehicles on shallow slopes in [16].) Second, there may be
a speed or power limitation on the mobile agent. If we also have a minimum
specified velocity for traversal, we can substitute
. (This was experimentally confirmed
within 2% for wheeled vehicles on shallow slopes in [16].) Second, there may be
a speed or power limitation on the mobile agent. If we also have a minimum
specified velocity for traversal, we can substitute ![]() for
for ![]() in the
preceding.
in the
preceding.
Third, there may be a danger of loss of traction on a steep surface. Traction
is controlled by the coefficient of static friction ![]() which is different
from the
which is different
from the ![]() coefficient
of kinetic friction (or rolling friction for a wheeled vehicle). This static
friction must equate all the force being used to push the agent forward, and
its maximum is
coefficient
of kinetic friction (or rolling friction for a wheeled vehicle). This static
friction must equate all the force being used to push the agent forward, and
its maximum is ![]() ,
so an anisotropic traction-loss phenomena will occur when the slope is greater
than (after some algebraic rearrangement) approximately
,
so an anisotropic traction-loss phenomena will occur when the slope is greater
than (after some algebraic rearrangement) approximately ![]() .
.
Fourth, we may experience a catastrophic overturn of the mobile agent on slopes more than a certain steepness. Such overturns occur when the projection of the center of gravity of the agent on the terrain surface lies outside the polygon formed by its support points [5], most often when the vehicle is "sideslope" or perpendicular to uphill. This is an anisotropic phenomenon because the distance of the projection of the center of gravity on a level surface from the boundaries of the support polygon determines the stability when the uphill gradient is oriented in that direction; for instance, a long truck is more stable going uphill than going sideslope. We cannot give a single formula for the anisotropism here because this is specific to the support pattern.
The first three cases above rule out a range of uphill traversal, and the
fourth a range of sideslope traversal (while braking phenomena affect a range
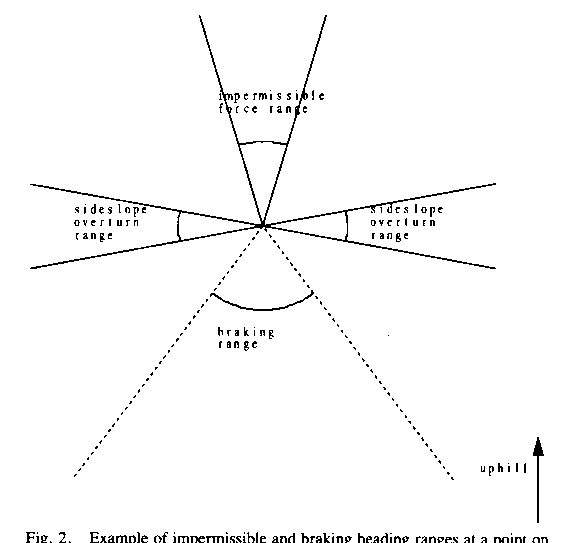
of downhill traversal). Figure 2 gives an example of the heading ranges
concerned. Note the impermissibility constraints can rule out unconnected
ranges of headings. Or some of their impermissible ranges may overlap, in which
case two critical-impermissibility headings disappear and one larger
impermissibility range is created. In some cases all possible headings may be
impermissible, giving an isotropic obstacle, the familiar kind in path-planning
work.
Somewhat similar anisotropisms arise with time-minimal paths when power is assumed constant. Now the maximum-power constraint does not apply but the velocity-minimum does. Slippage and overturn phenomena are identical to those with energy-minimizing paths.
Related work
The most similar major approach to this problem with which we are familiar is the grid-based one of [3]. Their cost function is much more arbitrary: it is discontinuous with heading, which is hardly reasonable, and the discontinuity, which represents the transition to braking, occurs exactly at sideslope, which is not reasonable on off-road terrain when friction is high. They also seem to ignore the viewing-angle cosine correction described earlier, so their results may be wrong on terrain with nonnegligible slopes.
[9] reports an integrated grid-based path-planning system that uses an anisotropic cost function incorporating a variety of factors. But it seems ad hoc, and no justification for it is given in the paper, nor are any other justifying papers cited.
The Army Mobility Model [18] uses a complicated formula for assigning traversal costs to terrain, and slope is a parameter. However, the Model averages slope in all directions to obtain an average figure for a terrain region, resulting in an isotropic model.
Turn criteria for optimal paths
We now specify local criteria for optimal paths. We will show there are only
four ways an optimal path can traverse a homogeneous-friction-coefficient
planar anisotropic region (henceforth called just a "region"): type
I, straight across at a permissible nonbraking non-critical heading, turning on
boundaries according to standard weighted-region constraints [15]; type II,
straight across at a critical-impermissibility heading to follow as close as
possible to a desired direction; type III, "switchbacks" or
"slaloming" alternating arbitrarily between a matched pair of
critical-impermissibility headings; and type IV, straight across with braking
at a non-critical heading, with the associated braking cost function. Other key
results of this section are summarized in Figures 3, 4, and 5. Figure 3
illustrates the four traversal types; Figure 4 gives their properties; and
Figure 5 summarizes the transition constraints between traversal types on the
boundary between two polyhedral facets (two regions of different surface
orientation), the most complicated aspect of our analysis.
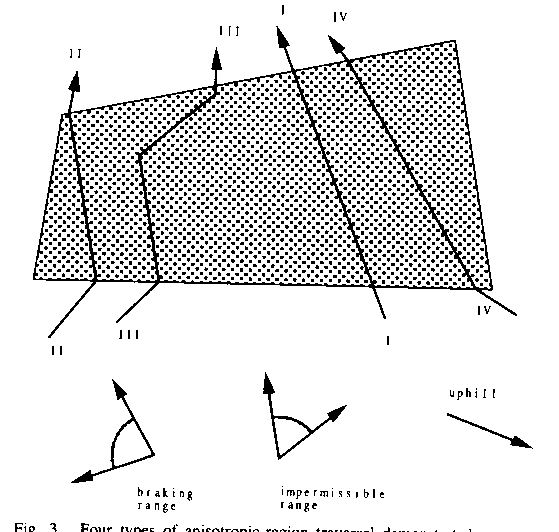
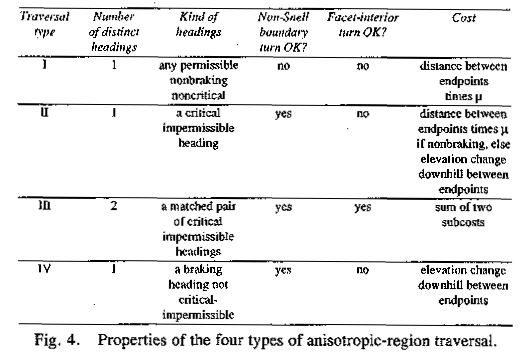
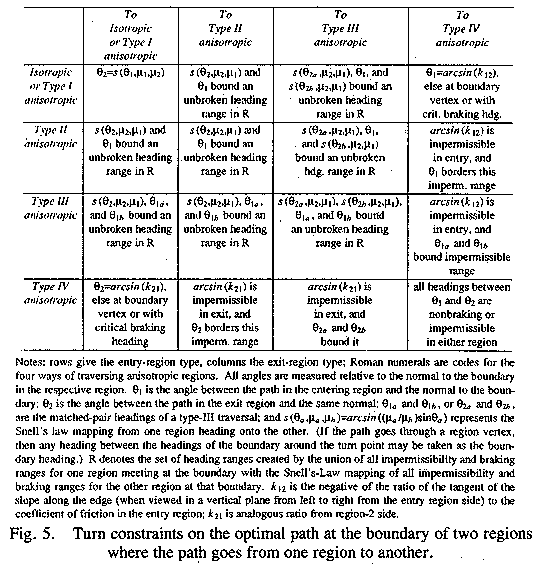
Basic definitions and results
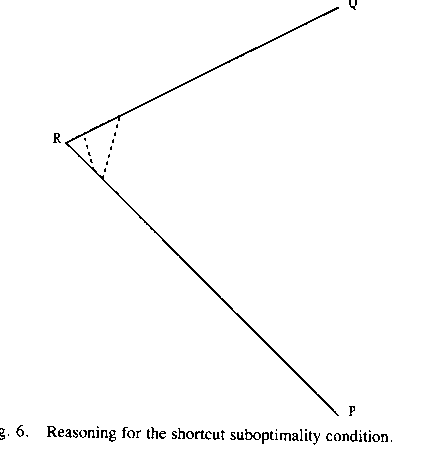
Definition: a shortcut is a straight-line segment across a turn on a two-line-segment path P connecting a point on one segment of P with a point on the other segment of P.
In what follows we will exploit the following necessary condition for
optimal paths ("Shortcut Suboptimality Condition"): whenever the
optimal path turns, it could never be improved by a shortcut across the inside
the turn. This is illustrated in Figure 6: if the optimal path from P to Q
makes a single turn at R, then the path that starts at P and takes a shortcut
must either be impossible due to constraints in the terrain traversed by the
shortcut, or the shortcut must cost more than its detour through R. Note any
shortcut must have a heading between the two path headings, the heading from P
to R and the heading from R to Q. We will also consider more complex ways of
improving on a path that turns, as in Lemmas 3.1 and 3.2.
Definition: Let ![]() be the Snell's-Law mapping of
heading
be the Snell's-Law mapping of
heading ![]() when
going from a region of cost-per-distance
when
going from a region of cost-per-distance ![]() to one of
to one of ![]() , where
, where ![]() and
and ![]() are angles
with respect to the normal of the boundary crossed; that is, the
are angles
with respect to the normal of the boundary crossed; that is, the ![]() if it
exists. (Note that
if it
exists. (Note that ![]() and the function is reversible
by interchanging the last two arguments:
and the function is reversible
by interchanging the last two arguments: ![]() .)
.)
Lemma 3.1: Suppose a path P turns from a heading (with respect to the
boundary normal) of ![]() in region 1 to a heading of
in region 1 to a heading of ![]() in region
2, and at least one part of P is nonbraking. This path cannot be optimal if
there exists a heading
in region
2, and at least one part of P is nonbraking. This path cannot be optimal if
there exists a heading ![]() between
between ![]() and
and ![]() such
that both
such
that both![]() is permissible and nonbraking in region 1, and
is permissible and nonbraking in region 1, and ![]() is permissible and
nonbraking in region 2. Proof: If such a
is permissible and
nonbraking in region 2. Proof: If such a ![]() exists, and the portions of
path P in the two regions are nontrivial, there must exist two points A and B
on P, A in region 1 and B in region 2, such that traveling from A at heading
exists, and the portions of
path P in the two regions are nontrivial, there must exist two points A and B
on P, A in region 1 and B in region 2, such that traveling from A at heading ![]() , and then turning
to heading
, and then turning
to heading ![]() on
the region border, will reach B. That is because if
on
the region border, will reach B. That is because if ![]() is left of
is left of ![]() , a path with
starting heading infinitesimally to the right of
, a path with
starting heading infinitesimally to the right of ![]() and turning by Snell's Law on
the boundary must have a heading to the left of
and turning by Snell's Law on
the boundary must have a heading to the left of ![]() in region 2, and hence can
intersect P arbitrarily close to the boundary. The argument is analogous for
in region 2, and hence can
intersect P arbitrarily close to the boundary. The argument is analogous for ![]() to the
right. Thus by picking A and B sufficiently close to the region boundary, it is
always possible to find a locally-optimal path obeying Snell's Law and
departing at
to the
right. Thus by picking A and B sufficiently close to the region boundary, it is
always possible to find a locally-optimal path obeying Snell's Law and
departing at ![]() that
connects A and B on the
that
connects A and B on the ![]() -
-![]() path. Since Snell's-Law paths are
the single local optimum among isotropic-weighted-region paths as proved in
[11] and [15] the
path. Since Snell's-Law paths are
the single local optimum among isotropic-weighted-region paths as proved in
[11] and [15] the ![]() path must be optimal if the
path must be optimal if the ![]() -
-![]() path is totally
nonbraking. Otherwise, if either segment of the latter path is braking, then
its cost can only be worse by Lemma 2.1, so the
path is totally
nonbraking. Otherwise, if either segment of the latter path is braking, then
its cost can only be worse by Lemma 2.1, so the ![]() path is still optimal.
path is still optimal.
Lemma 3.2: Suppose a path P turns from a heading (with respect to the
boundary normal) of ![]() in region 1 to a heading of
in region 1 to a heading of ![]() in region
2, and at least one part of P is nonbraking. This path cannot be optimal if
there exist headings
in region
2, and at least one part of P is nonbraking. This path cannot be optimal if
there exist headings ![]() and
and ![]() such that
such that ![]() ,
, ![]() ,
, ![]() is
braking in region 1, and
is
braking in region 1, and ![]() is braking in region 2. It
also cannot be optimal if
is braking in region 2. It
also cannot be optimal if ![]() ,
, ![]() ,
, ![]() is braking in the first
region, and
is braking in the first
region, and ![]() is
braking in the second region. Proof: Under either of the specified
conditions, P could not be any better than a detour path Q that starts on P
infinitesimally close to the boundary in region 1, follows heading
is
braking in the second region. Proof: Under either of the specified
conditions, P could not be any better than a detour path Q that starts on P
infinitesimally close to the boundary in region 1, follows heading ![]() to the
boundary, and then follows
to the
boundary, and then follows ![]() back to P, because such a path
would be braking its entire length. Consider the portion of P that is detoured
by Q. If it were entirely braking it would cost the same as Q. Otherwise, if
part of it were nonbraking, its total cost would be more than the all-braking
cost by Lemma 2.1.
back to P, because such a path
would be braking its entire length. Consider the portion of P that is detoured
by Q. If it were entirely braking it would cost the same as Q. Otherwise, if
part of it were nonbraking, its total cost would be more than the all-braking
cost by Lemma 2.1.
Lemma 3.3: If an optimal path turns within a region, it must turn from a critical impermissibility heading to its matching critical impermissibility heading on the other side of the impermissible heading range. Proof: Use the Shortcut Suboptimality Condition. Any shortcut across such turns must be either impossible or higher-cost-per-distance. It could not be higher-cost if it were braking, by the same argument used in Lemma 3.2: (1) if the detour around the shortcut were braking, it would have the same regular (first-order) cost, but have a turn and hence be undersirable in second-order cost; (2) if the detour is partly nonbraking, that can only increase the cost over the case (1) cost by Lemma 2.1. Hence turns are not desirable on an optimal path within a region unless all shortcuts across the turn are at impermissible headings. This can only be if the entire heading range between the two turn headings is impossible. Hence the two headings of the turn must be a matched pair of critical-impermissibility headings.
Isotropic traversals and anisotropic traversals of type I
As in our previous work [14, 15], we will specify local criteria that an optimal path must obey. First consider isotropic regions. As we have shown in previous work [12, 15, 11], optimal paths in such regions must be straight line segments, with turns only possible on the boundaries of such regions such that the turn obeys Snell's Law, with special modifications necessary at boundary vertices. Identical conditions apply to type-I traversal of anisotropic regions, which we will define as traversal at a non-critical nonbraking heading. Lemma 3.3 requires that a type-I traversal cannot be followed on an optimal path by a turn within a region, or be preceded by such a turn, because the only possible optimal turns involve type-II headings. The following theorem establishes conditions on region boundaries.
Theorem 3.1: A transition between two type-I traversals on the boundary of a region must obey the standard Snell's Law conditions of the isotropic-region case. Proof: the type-I headings by definition must not be infinitesimally close to impermissible or braking headings on both sides. Thus, no matter which direction the turn would be, it could be improved upon in the manner of Lemma 3.1 unless either (1) the turn followed Snell's Law or (2) the path went through a boundary vertex and followed the modification of Snell's Law for there.
Paths in isotropic regions and type-I anisotropic traversals can also "graze" regions, turning at a region vertex to avoid some adjacent region. The Shortcut Suboptimality Condition requires that such avoidance turns enclose either (1) a higher-cost isotropic region or (2) an anisotropic region in which all headings between those on the path before and after the turn are impermissible or braking.
Anisotropic-region traversals of type II
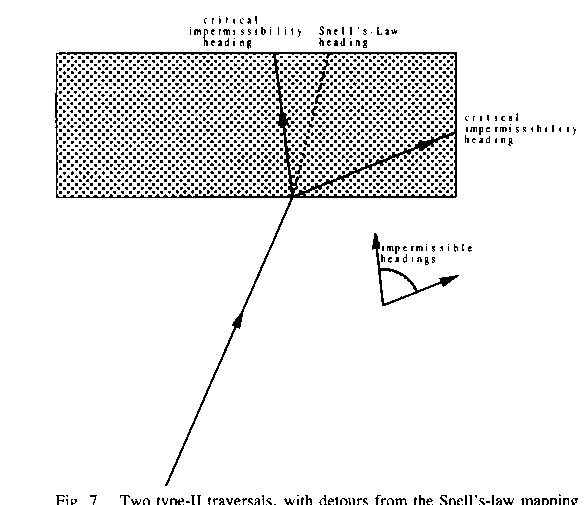
But suppose that obeying Snell's Law on a path entering an anisotropic
region would mean an impermissible heading in that region (see Figure 7). The
next best thing would seem to be "rounding" that impermissible
heading to either one of the matched pair of critical-impermissibility headings
surrounding the originally postulated heading. A path could traverse the region
at that critical-impermissible heading, and then turn back in the direction it
wanted to go originally--a small detour, but sometimes not much. That is a type
II traversal. Note type-II paths can be braking as well.
Theorem 3.2: Transitions between type-I and type-II traversal can only
occur (1) on region boundaries; (2) when the Snell's-Law mapping of the type-I
heading is impermissible or braking in the type-II region; (3) when every
heading between starting heading and the Snell's Law reverse mapping of the
ending heading is either (a) impermissible or braking in the first region, or
(b) its Snell's-Law mapping is impermissible or braking in the second region;
and (4) when there are no braking headings ![]() for the first region and
for the first region and ![]() for the
second region such that
for the
second region such that ![]() and
and ![]() are in opposite
senses (clockwise vs. counterclockwise) with respect to their corresponding
entry and exit path headings. Proof: Such turns cannot occur within regions
by Lemma 3.3, which explains condition (1). On a boundary, there must be some
reason a Snell's-Law detour as described in Lemma 3.1 is not possible, so
either one segment of such a detour must be impermissible or else one segment
must be braking. Hence condition (3) follows, and condition (2) is the special
case of (3) due to the definition of a type-I heading. Condition (4) follows
from Lemma 3.2.
are in opposite
senses (clockwise vs. counterclockwise) with respect to their corresponding
entry and exit path headings. Proof: Such turns cannot occur within regions
by Lemma 3.3, which explains condition (1). On a boundary, there must be some
reason a Snell's-Law detour as described in Lemma 3.1 is not possible, so
either one segment of such a detour must be impermissible or else one segment
must be braking. Hence condition (3) follows, and condition (2) is the special
case of (3) due to the definition of a type-I heading. Condition (4) follows
from Lemma 3.2.
Theorem 3.3: Transitions between two type-II traversals can only occur subject to conditions (1), (3), and (4) in Theorem 3.2 if at least one heading is nonbraking. If both headings are braking, the conditions are given by Theorem 3.8. Proof: Use the same arguments in Theorem 3.2 for the first case, noting now the properties of type-I traversal cannot be exploited to prove condition (2). For the all-braking second case, the conditions on Theorem 3.8 are satisfied.
Type-II paths can cross boundaries at vertices. However, type-I with type-II transitions through vertices can be handled by the methods for type-I paths through vertices discussed in [11] and [15], and type-II with type-II transitions require such a rare coincidence in two numeric quantities that we will ignore them.
Anisotropic-region traversals of type III
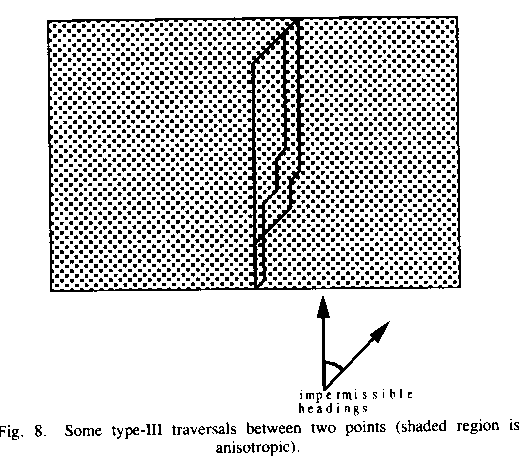
Optimal paths can also turn within anisotropic regions, what we call type-III
traversals. For instance, to go up a hill too steep to assault head-on, one can
"zigzag" up it in a series of switchbacks. This is possible when
transitory occurrence of an impermissible heading in the mobile agent is not
dangerous, as when the agent's momentum counters the danger. Lemma 3.3 says
that the only optimal such turns are from one critical impermissibility (or
type-II) heading to its matching critical impermissibility heading. Since a
vector sum is involved, the heading segments may be interleaved arbitrarily
without changing the cost (note the three paths in Figure 8 have identical
cost), so an infinite number of type-III paths are optimal with respect to
first-order cost. To minimize second-order cost, we should use the path with
the fewest turns, but that refinement is not essential. Note that if a region
has more than one disjoint range of impermissible headings, there can be
multiple kinds of type-III traversals, one for each; and the switchback turns
can be on region boundaries ("reflection" switchbacks). Note also one
heading in a type-III traversal can be braking.
Theorem 3.4: Transitions on region boundaries involving type-III traversals are constrained in the same way as those involving type-II traversals, but where the type-II headings referred to previously can be either of the defining matched-pair headings in its region. Proof: the type-III traversal(s) can terminate at the boundary with either of their defining headings, so either may be taken as the incident heading in a type-II transition. Note that all the conditions on type-II turns refer to the headings immediately adjacent to the boundary, and are not affected by what happens elsewhere on the path.
Anisotropic-region traversals of type IV
Anisotropic-region traversals with braking but without critical impermissibility are type IV. The following are the necessary results.
Theorem 3.5: Optimal paths including Type-IV traversals can not turn within a region. Proof: This follows immediately from Lemma 3.3, since a type-IV heading can not be a critical impermissibility one.
Theorem 3.6: Let ![]() be the coefficient of friction
for a type-I traversal, and let
be the coefficient of friction
for a type-I traversal, and let ![]() be the elevation inclination
angle of the facet edge at the meeting of two polyhedral facets as viewed from
the type-I side. Then transitions on a boundary between the type-I and a
type-IV traversal require that the type-I heading be either (1) permissible,
nonbraking, and form angle
be the elevation inclination
angle of the facet edge at the meeting of two polyhedral facets as viewed from
the type-I side. Then transitions on a boundary between the type-I and a
type-IV traversal require that the type-I heading be either (1) permissible,
nonbraking, and form angle ![]() with the normal to the boundary
(that angle being to the same side of the normal as the type-IV heading); or
(2) only if item (1) does not exist, a heading passing through a boundary
endpoint; or (3) only if item (1) does not exist, a permissible critical
braking heading. Furthermore, either the type-IV heading is critical-braking or
else no path at a braking heading could cross the boundary from the type-I
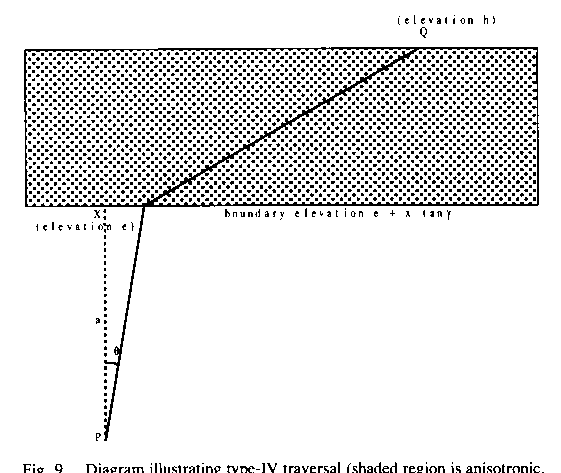
region. Proof: Consider the cost of a path from some point P a distance
"a" from the boundary in the non-braking region to some other point Q
in the braking region at elevation "h" (see Figure 9). Let the
elevation of the edge line be
with the normal to the boundary
(that angle being to the same side of the normal as the type-IV heading); or
(2) only if item (1) does not exist, a heading passing through a boundary
endpoint; or (3) only if item (1) does not exist, a permissible critical
braking heading. Furthermore, either the type-IV heading is critical-braking or
else no path at a braking heading could cross the boundary from the type-I
region. Proof: Consider the cost of a path from some point P a distance
"a" from the boundary in the non-braking region to some other point Q
in the braking region at elevation "h" (see Figure 9). Let the
elevation of the edge line be ![]() , where d is elevation of the
projection of P onto the edge, and x is distance along the edge when viewed
from above. Let
, where d is elevation of the
projection of P onto the edge, and x is distance along the edge when viewed
from above. Let ![]() be
the path angle in the nonbraking region with respect to the normal to the edge
when viewed from above. Then the cost of the path from P to Q (necessarily straight
except for a turn on the boundary) is
be
the path angle in the nonbraking region with respect to the normal to the edge
when viewed from above. Then the cost of the path from P to Q (necessarily straight
except for a turn on the boundary) is ![]() . Its derivative with respect to
. Its derivative with respect to ![]() is
is ![]() , which is zero
only when
, which is zero
only when ![]() ,
a single value. This value is a strict minimum because the second derivative
there is
,
a single value. This value is a strict minimum because the second derivative
there is ![]() which
is always positive. If such a heading does not exist, i.e.
which
is always positive. If such a heading does not exist, i.e. ![]() , or the heading is not a
type-I heading, the optimal path must represent an extremum of possibilities,
which means case (2) or (3) in the theorem statement. (Note the Snell's-Law
mapping function is not involved here because the arcsin formula supplants it.)
The last condition in the theorem comes from Lemma 3.2: If the type-IV heading
were not critical-braking, then there must exist headings both just to the left
and just to the right of it that are braking in the type-IV region. Hence the
path could be improved by some detour from a point on the path in the type-I
region infinitesimally close to the boundary to a point on the path in the
type-IV region infinitesimally close to the boundary, an all-braking detour
using a braking heading for the type-I region and a heading just to the left or
just to the right of the original type-IV heading for the type-IV region.
, or the heading is not a
type-I heading, the optimal path must represent an extremum of possibilities,
which means case (2) or (3) in the theorem statement. (Note the Snell's-Law
mapping function is not involved here because the arcsin formula supplants it.)
The last condition in the theorem comes from Lemma 3.2: If the type-IV heading
were not critical-braking, then there must exist headings both just to the left
and just to the right of it that are braking in the type-IV region. Hence the
path could be improved by some detour from a point on the path in the type-I
region infinitesimally close to the boundary to a point on the path in the
type-IV region infinitesimally close to the boundary, an all-braking detour
using a braking heading for the type-I region and a heading just to the left or
just to the right of the original type-IV heading for the type-IV region.
Theorem 3.7: For a transition on a boundary between a type-II and a
type-IV traversal, the type-II heading (nonbraking by definition) must bound
the impermissible range of headings that includes the ![]() heading. Proof:
since the proof of Theorem 3.6 showed that special heading is the single local
minimum of the cost formula, if that heading is not possible the true minimum
must occur at the limit of a feasibility region adjacent to the special
heading, which here is the type-II headings bounding the impermissibility
region of that special heading.
heading. Proof:
since the proof of Theorem 3.6 showed that special heading is the single local
minimum of the cost formula, if that heading is not possible the true minimum
must occur at the limit of a feasibility region adjacent to the special
heading, which here is the type-II headings bounding the impermissibility
region of that special heading.
Theorem 3.8: At a turn on a boundary between two type-IV traversals, (1)
both headings must be impermissible or nonbraking in the opposite region, (2)
all intermediate headings must be impermissible or nonbraking in at least one
region, (3) some intermediate heading must be a critical-braking or
braking-critical-impermissible (braking and type-II) for each region, and (4)
the aforementioned critical heading for the entry region must be closer to the
entry heading than the aforementioned critical heading for the exit region is
to the entry heading. Proof: Use the Shortcut Suboptimality Condition. If a
shortcut across the two type-IV segments consists of two (as created by the
boundary) braking segments itself, then the elevation-difference cost is
identical on both paths, but the detour is worse in second-order cost and hence
undesirable. So type-IV to type-IV transition turns are optimal only if every
shortcut across them is partly nonbraking or partly impermissible, giving
condition (2) in the theorem statement. Taking that to the limit proves
condition (1), since it is known that the path headings themselves are braking.
Hence if heading ![]() in either region is known to be
braking and heading
in either region is known to be
braking and heading ![]() in that same region is known to
be nonbraking or impermissible, there must exist some heading between
in that same region is known to
be nonbraking or impermissible, there must exist some heading between ![]() and
and ![]() that is a
critical braking heading or a braking-critical-impermissibility heading, by
their definitions, proving condition (3). Condition (4) occurs because the two
braking-heading ranges for the two regions cannot overlap by condition (2).
that is a
critical braking heading or a braking-critical-impermissibility heading, by
their definitions, proving condition (3). Condition (4) occurs because the two
braking-heading ranges for the two regions cannot overlap by condition (2).
Completeness of the traversal types
Theorem 3.9: The four traversal types described are the only ways an optimal path can traverse polyhedral terrain subdivided into regions of homogeneous cost-per-distance, given the model of Section 2. Proof: A straight path segment in a region must be either braking (type IV or braking type II by definition) or nonbraking; nonbraking traversal must either avoid critical impermissibility headings (type I) or not. Lemma 3.3 requires that type-I or type-IV paths cannot turn within regions. Theorems 3.2, 3.3, and 3.4 require that the only way critical impermissibility headings can be used on an optimal path is either by paths not turning in the region (type II) or turning between a matched pair of such headings (type III).
Isotropic obstacles
Isotropic obstacles, regions in which no traversal is possible at any heading, have been studied extensively in the context of many robot path-planning problems. It is straightforward to include them in our approach, modeling their boundaries as polygons just like all other regions. By the Shortcut Suboptimality Condition, any optimal path that turns on the boundary of an obstacle must enclose an obstacle vertex in the turn angle. A path can also touch an obstacle without turning if it follows along an obstacle edge.
Reducing path-finding to A* search
For our now-formalized problem, the optimal path between a start and a goal point can be found by A* search. This search need only consider a finite number of possibilities when region boundaries are polygonal, as with the polyhedral-obstacle algorithms of [4] and [17], thanks to the results of the last section and the convexity proof given in the Appendix. This proof shows that for certain well-behaved subspaces of the space of paths between start and goal, there is at most one local-optimum path; hence it can be found by simple iterative optimization with bisection. The well-behaved path subspace required for this theorem is any set of paths crossing the same region-boundary-edge "windows" in the same order and with the same traversal types and subtypes; a "window" can be any region edge or region vertex, and a traversal subtype is a type qualified by the particular heading(s) involved in types II or III (there are no subtypes of I and IV). For example, for an anisotropic region characterized by Figure 2, with three impermissible-heading ranges and a braking range that does not overlap the impermissible-heading range, there are eleven types and subtypes: one type I, six type II, three type III, and one type IV.
The A* search is over all window sequences in the same way as [12, 15]. For
those window sequences that terminate at the goal, we can compute the
locally-optimal path, and take the minimum-cost of these as the global optimum.
This may seem much work for complicated terrain, but many pruning criteria
follow from the boundary constraints discussed in Section 3. Any feasible path
between start and goal provides an upper bound on the cost of the optimal path,
and that prunes high-cost window sequences; we can obtain a feasible path by
running a straight line between start and goal, and locally perturbing segments
of that line until it avoids obstacles and does not violate anisotropic-region
constraints. We can also rank window sequences by the sum of a lower bound on
their cost plus a cost-to-goal lower bound from the last window in the
sequence. A lower bound on the cost of a window sequence is obtained by adding
the region's ![]() times
the minimum distance across the region for type I, II, and III traversals, or
the minimum elevation difference across the region for type-IV traversals. The
cost-to-goal lower bound is just distance to the goal when the window is a
point; for an edge, it is the distance to the goal of the closest of three
points: the two endpoints, and the perpendicular projection of the goal onto
the edge if any.
times
the minimum distance across the region for type I, II, and III traversals, or
the minimum elevation difference across the region for type-IV traversals. The
cost-to-goal lower bound is just distance to the goal when the window is a
point; for an edge, it is the distance to the goal of the closest of three
points: the two endpoints, and the perpendicular projection of the goal onto
the edge if any.
Visibility analysis
But the most powerful pruning tools are the implicit vertex-visibility and edge-visibility graphs [4] for the anisotropic regions, graphs that indicate when straight lines can connect region vertices or region-boundary edges without intersecting others. Such graphs are straightforward to make once all regions are subdivided into convex subregions. The artificial boundaries introduced in subdivision can be flagged as special and treated as permitting no turns when encountered in the path search.
Visibility analysis can be further improved by considering the possible headings with which an optimal path could cross a window. For each window in a window sequence created during A* search, we can calculate its "shadow" on the next, based on the possible range of headings of the current and previous region traversals. If the next window is an edge, the intersection of the edge with the shadow is the only part of the edge reachable, and this smaller edge narrows the subsequent window sequence; if the intersection is empty, the entire window sequence is impossible. In computing shadows, Type II traversal is easy because the traversal heading is fixed, making the shadow on the exit line a simple linear mapping of the shadow on the entrance edge. For Type III traversal, the path displacement between the two edges must represent a weighted sum of two fixed vectors, so project the leftmost of those vectors from the left side of the entry window, and project the rightmost of those vectors from the right side of the entry window, to obtain the shadow. For Type IV, project the bounding headings of the braking range. For Type I, a variety of shadow constraints apply depending on the traversal types of the adjacent regions; for instance, if two adjacent regions are both traversed by type-I paths, the Snell's Law mapping of the first heading range is the heading range of the second.
Shadows can propagate backward as well as forward, leading to constraint propagation as the term is used in artificial intelligence. For instance, when a type I traversal is followed by a type IV, the type I is restricted to at most four distinct headings, as is the traversal just before the type I, and so on back to the start point. Such backward propagation is particularly helpful when started from the goal point.
Implementation
We are testing a Common Lisp implementation [13] of our algorithm, using
data about three military vehicles, two light trucks and an armored personnel
carrier (a tracked vehicle). For such vehicles, isotropic soil failure occurs
before anisotropic power limitations, so the only significant anisotropic
phenomena are braking and sideslope-overturn failure. Furthermore, for these
particular vehicles, turns are slow and hence type-III turns are unsafe. Thus,
our implementation only needed to consider traversals of types I, II, and IV in
optimal paths. Also note the impermissibility of sideslope traversal on even
small inclines means that the ![]() cost term is especially
negligible, since the eliminated headings are those in which the term most
matters.
cost term is especially
negligible, since the eliminated headings are those in which the term most
matters.
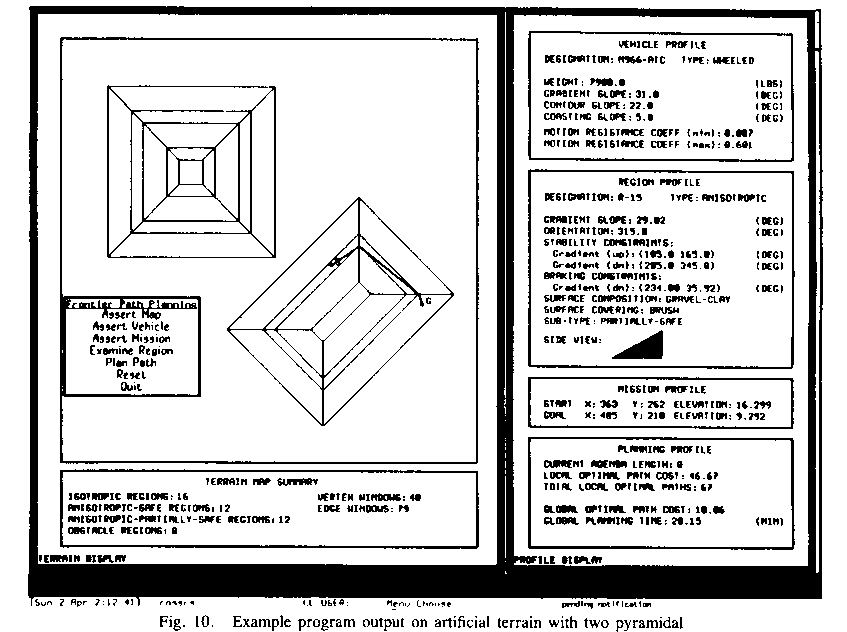
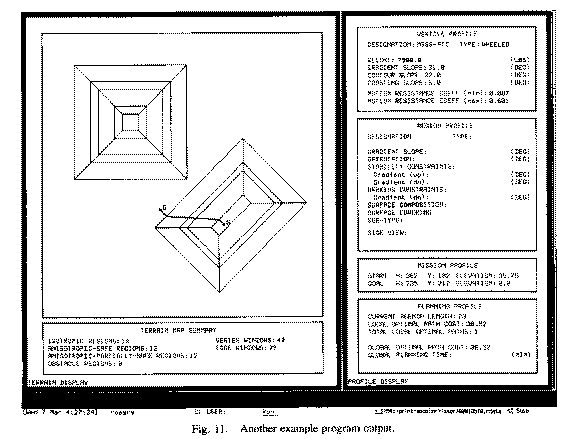
Figures 10, 11, and 12 show sample program output screens, for problems on
artificial terrain with a uniform coefficient of friction. The terrain contains
two pyramidal hills of varying slopes, as illustrated in the side views in
Figure 13. The vehicles assumed were two kinds of cargo truck, and the "vehicle
profile" box in the upper right shows data on them; the "gradient
slope" is the maximum slope in degrees on which truck can travel in some
direction, the "contour slope" is the minimum sideways (sideslope)
inclination of the truck that can cause sideslope overturn, and the
"coasting slope" is the minimum slope at which braking is necessary
when heading straight downhill. Reasoning times averaged 23 minutes, which is
reasonable considering we have not attempted an efficient implementation. The
implementation is described in detail in [13].


As formulated, our path-planning problem is another instance of what [17]
calls the "combinatorial shortest path problem." Such problems occur
when an optimal permutation of edge or vertex sequences in a graph must be
found to solve a problem. Though some special subcases are polynomial-time, as
well as some key components like finding line intersections [2], the time for
the general problem is ![]() in time where n is the number
of vertices in the terrain area under consideration. (This result assumes the
iterative solution of the optimization through every window sequence requires
constant time.) For these problems, the space complexity is similar to the time
complexity. This result is for worst-case analysis; the multitude of pruning
heuristics we have given means that our algorithm can be much better on the
average than this pessimistic bound.
in time where n is the number
of vertices in the terrain area under consideration. (This result assumes the
iterative solution of the optimization through every window sequence requires
constant time.) For these problems, the space complexity is similar to the time
complexity. This result is for worst-case analysis; the multitude of pruning
heuristics we have given means that our algorithm can be much better on the
average than this pessimistic bound.
Thus the algorithm of this paper can only be desirable on a time or space basis compared to grid-based methods if a significant data compression of the terrain can be done in polyhedral modeling, so that n is far smaller than the number of cells in a sufficient-resolution grid. This means terrain with usually-low values of the second derivative of the elevation, as for instance, terrain consisting of ridges with sharp curvatures only at their crests. But even when time and space for an implementation of our algorithm are large, it may still be highly desirable on the basis of solution quality. As we discussed in Section 1, grid-based methods when used with anisotropic cost functions will round headings to a elements of a fixed set, and these errors can accumulate; our paths follow the exactly optimal headings. We also observed in computer experiments that grid-based methods have a more serious problem of failing to find any path at all for goals reachable only at headings close to impermissible. For instance, if there are eight directions of grid propagation, and the sideslope-impermissibility headings ranges in a planar region are between 90 and 180 degrees each, the grid propagation will be unable to find any paths except those straight uphill or downhill; and even if the sideslope-impermissibility heading ranges are between 0 and 90 degrees, an average of one quarter of all possible goal headings will be achievable only by paths that we would classify as type-III, paths that cannot be smoothed because the result would be an impermissible path. Thus we feel our algorithm will be more appropriate than grid-based methods whenever sufficient time is available, as in planning an army operation in advance.
Constructing a polyhedral terrain model
Our methods require a polyhedral approximation of terrain. The graphics literature contains much discussion of surface modeling, and this is not our research focus, so we will only discuss polyhedral modeling briefly here. Algorithms to obtain good, as opposed to adequate, polyhedral approximations (that is, exhibiting significant data compression over the raw elevation data) are complex and not always reliable. Finding a good polyhedral model can be viewed as an optimization problem where one strives to minimize both the number of polyhedral faces and the least-squares deviations of the fits on each face, but there are few heuristics to guide the optimization, and usually many local optima [19]. Testing all possible groupings of known-elevation points into polyhedral faces is impossibly slow. Mere clustering of the terrain based on the gradient gets into trouble on terrain with gradual curvature. And the intersection line of two well-fit planes may not lie in azimuth projection between the two sets of points defining the planes. We achieved best success with the following four-step algorithm.
1. We only need to polyhedrally model terrain sufficiently steep to create anisotropic effects by our model, but not so steep as to be untraversable in any direction. This means terrain with a gradient magnitude between the braking inclination and the isotropic-failure inclination. So a first step extracts all such terrain points and clusters them; only these are considered in subsequent steps.
2. We classify these terrain points by curvatures in the X and Y directions into four classes: convex, concave, flat, or "other" (the curvature threshold being an adjustable parameter). We then cluster similarly-marked points into subregions of the regions in step 1. This improves the chances that the intersection planes created for adjacent sets of points will lie between the points, and is based on greater ease in finding a polyhedral fit for a convex or concave surface, thanks to the two-dimensional extension of Rolle's Theorem.
3. We then perform a split-and-merge algorithm (like Algorithm 6.6 in [10]) using the planar least-squares fit to the elevations as criterion. We subdivide the subregions recursively, approximately in half each time, until the region fit is below a threshold. We then merge adjacent regions wherever the fit remains below the threshold.
4. We then compute the intersection lines of all the least-squares planes for each pair of adjacent regions. We then iteratively adjust the orientations of the planes to minimize a weighted sum of the planar fits and the deviations of the intersection lines from their ideal positions; ideal positions are computed from region-border least-squares lines partitioning the original data points.
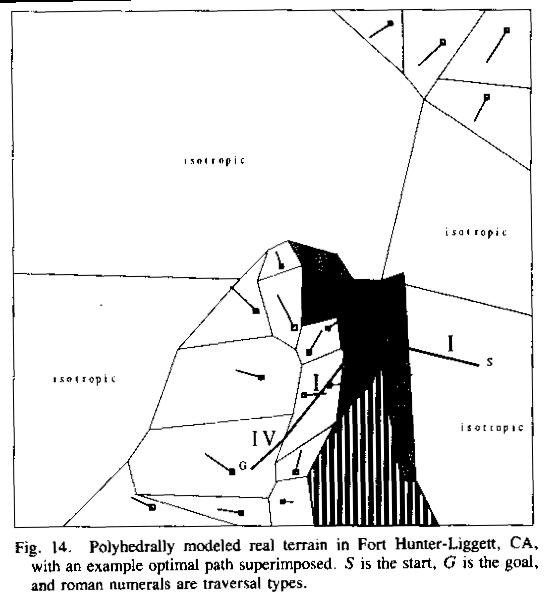
Figure 14 shows some hilly terrain near Lower Stony Reservoir, Fort Hunter-Liggett, California, as modeled polyhedrally by our method. (The user interface
used with real data is different from that shown previously.) A 40-by-40 grid
of elevation readings (obtained from digitizing a map) at 12.5-meter spacings
was used, plus some vegetation data. The figure shows portions of two hills
(bottom center and upper right) with a flat area between. There are 26
polyhedral facets, of which four are isotropic (meaning that their slopes are
all less than the braking slope), one is an obstacle (the vertically shaded
area at the bottom right, where the vegetation was dense and the slope was
steep), and five are high-cost but passable (the spotted regions, where
vegetation is a well-grazed oak forest; their traversal cost rate is assumed to
be 1.5 times the cost rate of the non-shaded regions). The gradient of the
anisotropic passable regions is indicated by the line segments within each
region: the length of each segment indicates gradient magnitude, and the
direction indicates gradient direction, with the square indicating the uphill
end of the segment. The slope at which sideslope danger occurs was 10 degrees,
and the slope at which braking occurs was 2 degrees. The thick solid line
crossing the figure is a sample optimal path; S is the start and G is the goal.
Conclusion
We have developed and demonstrated a new grid-free approach to finding optimal paths on terrain with arbitrary elevation variation. Our model addresses the two major forces acting along such paths, gravity and friction, and shows a surprisingly elegant way in which their complexities can be simplified. Our grid-free approach means that terrain features like hills and ridges are the basic units of our analysis, not arbitrarily-placed grid cells, so we may be able to save much time and space over grid methods on terrain whose features can be simply modeled. Reference to terrain features also makes our paths easier to follow in the real world. And furthermore, our methods can solve problems that grid methods cannot, and can give lower-cost paths than those of grid methods, even when the resolution of the grid is made arbitrarily fine. But a truly efficient implementation of our methods remains future work.
References
[1] M. G. Bekker, Introduction to Terrain-Vehicle Systems, Ann Arbor, MI: University of Michigan Press, 1969.
[2] J. L. Bentley and T. A. Ottmann, "Algorithms for reporting and counting geometric intersections," IEEE Transactions on Computers, C-28, 9, 643-647, September 1979.
[3] D. Gaw and A. Meystel, "Minimum-time navigation of an unmanned mobile robot in a 2-1/2D world with obstacles", Proceedings of the IEEE Conference on Robotics and Automation, 1670-1677, April 1986.
[4] T. Lozano-Perez and M. A. Wesley, "An algorithm for planning collision-free paths among polyhedral obstacles", Communications of the ACM, 22, 10, 560-570, October 1979.
[5] McGhee, R. and Iswandhi, G., "Adaptive Locomotion of a Multilegged Robot over Rough Terrain", IEEE Transactions Systems, Man, and Cybernetics, SMC-9, 4, 176-182, April 1979.
[6] J. S. B. Mitchell and D. Keirsey, "Planning Strategic Paths Through Variable Terrain Data", SPIE, Applications of Artificial Intelligence, volume 485, 172-179, 1984.
[7] J. S. B. Mitchell, D. M. Mount, and C. H. Papadimitriou, "The discrete geodesic problem", SIAM Journal on Computing, 16, 4, 647-668, August 1987.
[8] J. S. B. Mitchell and C. H. Papadimitriou, "The weighted region problem", to appear in Journal of the ACM, 1990.
[9] A. M. Parodi, "Multi-goal real-time global path planning for an autonomous land vehicle using a high-speed graph search processor", Proceedings of the 1985 IEEE Conference on Robotics and Automation, 161-167, 1985.
[10] T. Pavlidis, Graphics and Image Processing, Rockville, MD: Computer Science Press, 1982.
[11] R. Richbourg, "Solving a Class of Spatial Reasoning Problems: Minimal-Cost Path Planning in the Cartesian Plane", Ph. D. Thesis, U. S. Naval Postgraduate School, June 1987 (also Technical Report NPS52-87-021).
[12] R. Richbourg, N. Rowe, M. Zyda, and R. McGhee, "Solving Global Two-Dimensional Routing Problems Using Snell's Law and A* Search", Proceedings of the 1987 IEEE Conference on Robotics and Automation, Raleigh, North Carolina, 1631-1636, February 1987.
[13] R. S. Ross, "Planning Minimum-Energy Paths in an Off-Road Environment with Anisotropic Traversal Costs and Motion Constraints", Ph. D. Thesis, U. S. Naval Postgraduate School, June 1989.
[14] N. C. Rowe, "Roads, Rivers, and Rocks: Optimal Two-Dimensional Route Planning around Linear Features for a Mobile Agent", accepted to International Journal of Robotics Research, to appear 1990.
[15] N. C. Rowe and R. F. Richbourg, "An Efficient Snell's-Law Method for Optimal-Path Planning Across Multiple Homogeneous-Cost Regions", accepted to International Journal of Robotics Research, to appear 1990.
[16] A. A. Rula and C. J. Nuttall, An Analysis of Ground Mobility Models (ANAMOB)", Technical Report M-71-4, U.S. Army Engineer Waterways Experiment Station, Vicksburg, Miss., July 1971.
[17] M. Sharir and A. Schorr, "On shortest paths in polyhedral spaces," SIAM Journal of Computing, 15, 1, 193-215, February 1986.
[18] G. W. Turnage and J. L. Smith, "Adaptation and condensation of Army Mobility Model for cross-country mobility mapping," Technical Report GL-83-12, U. S. Army Corp of Engineers, Waterways Experiment Station, September 1983.
[19] D. Yee, "Three Algorithms for Planar-Path Terrain Modeling", M. S. thesis, U.S. Naval Postgraduate School, technical report NPS52-89-018, June 1988.
Appendix: The convexity theorem
Assume a two-dimensional world consisting of anisotropic and isotropic polygonal regions, each with a uniform coefficient of friction. We prove, over the set of all paths between some start and goal points that cross the same region-boundary edges in the same order, that path cost is a convex function of parameters sufficient to uniquely specify the path. The parameters will be distances along the region-boundary edges. We will first show that the cost of each subpath between region boundaries is convex. (We will do this proof for minimizing energy cost, but the analogous proof for minimizing time cost under constant power is very similar.) Since the coefficient of friction is constant for each subpath, we will ignore it. There are five cases to consider.
Case 1, beginning and ending segments of the path: first suppose the
segment traverses an isotropic region or does a type-I traversal of an
anisotropic region. Let x represent the distance along the first or last region
boundary from the projection of the start or goal point onto its line
extension, and assume this projection has length c. The cost between the start
or goal and this boundary is ![]() which has a second derivative
with respect to every other variable besides x of zero, and with respect to x
of
which has a second derivative
with respect to every other variable besides x of zero, and with respect to x
of ![]() , a
nonnegative quantity.
, a
nonnegative quantity.
For type III nonbraking traversal in either the beginning or ending path
segment, let ![]() and
and
![]() be
the two headings, D the distance of the start or goal point from the boundary,
and x the distance from the projection of the start or goal on the boundary to
the intersection of the path with the boundary. Then the cost (if both headings
are nonbraking) is
be
the two headings, D the distance of the start or goal point from the boundary,
and x the distance from the projection of the start or goal on the boundary to
the intersection of the path with the boundary. Then the cost (if both headings
are nonbraking) is
which is convex because it is a linear function of x. If one
heading is braking, that just multiplies its subcost by a constant factor, the
ratio of the negative of the slope tangent to ![]() , so linearity is preserved.
, so linearity is preserved.
Type II traversal for the first or last path segment need not be considered in the convexity analysis because its cost is fixed by the critical heading chosen. Type IV or type II braking-traversal cost is just a function of the elevation of the intersection point, which on a planar polyhedral face is a linear function of distance along the boundary, and hence is convex.
Case 2, general isotropic-region and anisotropic-type-I segments: if the
two boundaries are not parallel, let x and y be distances along the lines
containing the boundary line segments, distances from the intersection of those
lines. The law of cosines says that the subpath distance is ![]() . Convexity is
proved from
. Convexity is
proved from
by squaring both sides, cancelling terms, rearranging, squaring
again, and cancelling terms to get a nonnegative sum of squares; we skip the
tedious details. If the region boundaries are parallel at distance D, measure
the distances x and y along them relative to some perpendicular line. Then
subpath distance is ![]() . Convexity follows from
. Convexity follows from
which can be shown by the same methods as the general case.
Case 3, general type-II segments: if the boundaries are not parallel, then by the law of sines the ratio of this subdistance to the distance of the region entry point from the point of intersection of the linear extensions of the two boundary segments is a constant since it is equal to the ratio of constants for the triangle formed by the path and the two region boundaries: the sine of the angle between the two boundary segments and the sine of the angle at the second (exit) boundary. Hence whether or not the heading is braking, the cost can be expressed as ax+b, where x is distance along the first boundary line, a convex function of x; hence cost is a convex function of x. (If the boundaries are parallel, the cost is a constant independent of entry point, so its derivatives are zero.)
Case 4, general type-III segments: Tthe distance across the region
does not depend on the locations of the turn points, just the total subpath
length allocated to each of the two headings; call these ![]() and
and ![]() . As in case 2,
let x and y be distances of the entry and exit points from the intersection
point of the extension of the boundaries into lines. Let
. As in case 2,
let x and y be distances of the entry and exit points from the intersection
point of the extension of the boundaries into lines. Let ![]() and
and ![]() be the
headings of the two region boundaries, and
be the
headings of the two region boundaries, and ![]() and
and ![]() the two (known)
subpath headings. Then:
the two (known)
subpath headings. Then:
We can solve these equations for ![]() and
and ![]() , and the total
distance of the optimal path in the anisotropic region is:
, and the total
distance of the optimal path in the anisotropic region is:
This is a linear function of both x and y, and hence is
convex with respect to all boundary-distance variables. (That also covers
parallel boundaries, when ![]() .) If one subpath heading is braking,
that just multiplies its cost by a constant as in case 1, so linearity is
preserved.
.) If one subpath heading is braking,
that just multiplies its cost by a constant as in case 1, so linearity is
preserved.
Case 5, general type-IV segments: These segments must be straight, so we can use the same variables as case (2), distance along the boundaries. The virtual cost is proportional to the difference between the starting and ending elevations. But on a planar polyhedral face, the elevation along a boundary line segment is a linear function of distance along it. Therefore the difference in elevations is just the difference between two linear functions of two variables, and it must be convex in those variables. Parallelism of the boundary segments does not affect this argument.
Hence all the subcosts in a well-behaved subspace of paths are convex functions of the variables (distances along boundaries). Hence their sum is convex. It is true that some of the variables are functions of others (with several isotropic regions in succession, the first two boundary intersections determine all the others, by Snell's Law; with a type II anisotropic traversal, the first entry point determines the exit). However, a restriction of the domain of a convex function that makes some of the variables monotonic functions of the other variables is still convex. The functions here are monotonic because in the case of isotropic or type I anisotropic traversal, Snell's Law gives a monotonic nonlinear mapping of entry angle into exit angle, and hence, entry point onto exit point; and in the case of type II anisotropic traversal, the fixed heading of traversal forces a linear mapping of entry point onto exit point.
Convexity of total path cost means there is at most one path in the set of possible paths between start and goal that is a local minimum with respect to total cost. Hence the local minimum (if any) is the global minimum, and can be found by a simple bisection iteration.
Captions for figures
Figure 1: Summary of our physical model of the path-following agent
Figure 2: Example of impermissible and braking heading ranges at a point on a sloped plane; the six upper rays represent critical- impermissibility headings, the lower two critical-braking headings
Figure 3: The four types of anisotropic-region traversal, demonstrated across a quadrilateral sloped-planar region with friction coefficient homogeneous and identical to its surroundings
Figure 4: Properties of the four types of anisotropic-region traversal
Figure 5: Turn constraints on the optimal path at the boundary of two regions where the path goes from one region to another
Figure 6: Reasoning for the Shortcut Suboptimality Condition
Figure 7: Two type-II traversals, detours from the Snell's-Law mapping (shaded region is anisotropic with a higher coefficient of friction)
Figure 8: Some type-III traversals between two points (shaded region is anisotropic)
Figure 9: Diagram illustrating type-IV traversal (shaded region is anisotropic, assumed traversal type-IV)
Figure 10: Example program output on artificial terrain with two pyramidal hills of varying slopes (S is the start point, G the goal point)
Figure 11: Another example program output
Figure 12: Another example program output
Figure 13: Side view of the hills used in Figures 11, 12, and 13 (lower right hill is viewed from southwest; slopes in other directions on same hill are the same). Numbers are slopes in degrees. Vertical scale exaggerated by a factor of 2.
Figure 14: Polyhedrally-modeled real terrain in Fort Hunter-Liggett, California, with an example optimal path superimposed. S is start, G is goal, and Roman numerals are traversal types.