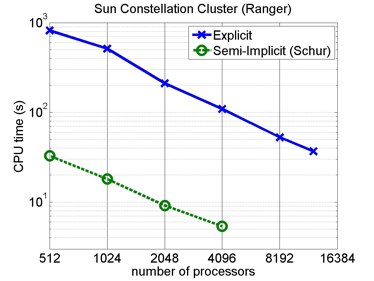
Scalability of NUMA

Continuous Galerkin version of NUMA

The results for NUMA-CG use both explicit (3rd order 5-stage Runge-Kutta) and semi-implicit (2nd order backward difference formula) time-integrators. The problem size is 64x64x64 4th order elements (total of 16 Million gridpoints).

NUMA Unified Numerics

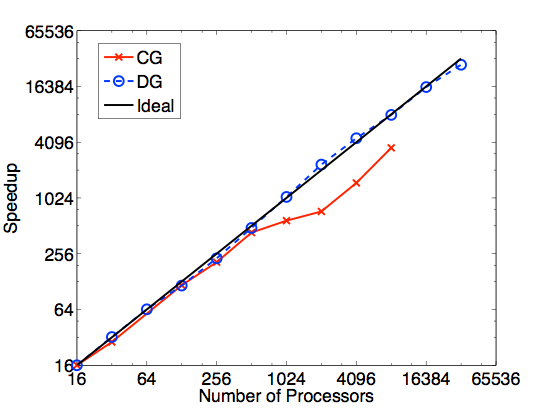
NUMA can use either continuous (CG) or discontinuous Galerkin (DG) methods. Both methods are high-order and highly scalable methods. In fact, below one can see that both versions of NUMA scale linearly on massively parallel computers.

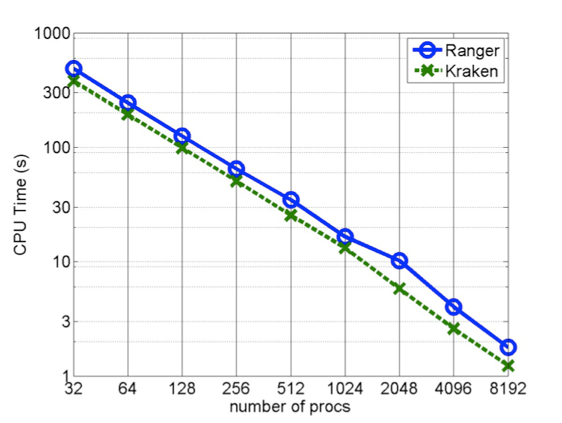
Discontinuous Galerkin version of NUMA

The results for NUMA-DG only use explicit (3rd order 5-stage Runge-Kutta) time-integration.

The problem size is 32x32x32 8th order elements (total of 16 Million gridpoints).

NUMA-CG and NUMA-DG

The results for NUMA-CG and NUMA-DG using both explicit (3rd order 5-stage Runge-Kutta) and semi-implicit (2nd order backward difference formula) time-integrators. The problem size is 64x64x64 4th order elements (total of 16 Million gridpoints).