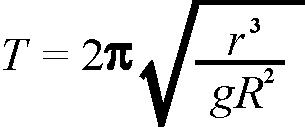
Press homepage
//Review//Catalog//Newport Papers//Reader servicesAlan R. Washburn
ACTUALLY, A COMPLETE IDIOT would have trouble with this tutorial. The real intended audience is scientifically oriented and pressed for time. The objective is to provide an acquaintance with the technology and terminology relevant to Earth-orbiting satellites. In spite of this mild ambition, however, the vocabulary expansion that follows is nontrivial. Terms that are used in a special sense—twenty four of them—are italicized when first defined. There is even a formula.
Reference System
The coordinate system used in this tutorial has its origin at the center of Earth. In this coordinate system the Sun goes around the earth, contrary to what you may have heard. There is actually no harm in this viewpoint, since the origin of coordinates can always be whatever is convenient. It is true that Earth would be an awkward origin if we were interested in the motion of other planets (since they have complicated orbits in Earth-centered coordinates), but the planets do not sensibly affect Earth satellites, the subject of interest here, so the center at Earth will do fine.
The problem is how to orient the x, y, and z axes. The z axis is easy; it will point to the North Pole along Earth's axis of rotation. We want to have a direction for the x axis that does not rotate with Earth, so that an observer could cling to the axis frame and see all the stars other than the Sun as stationary—an inertial frame of reference. There are many such directions. The convention is to orient the x axis in the direction of the vernal equinox (), which is by definition the direction to the Sun on the day in spring when day and night have the same length. Any time you can see the constellation Pleiades, you are looking approximately in the direction . Since is in Earth's equatorial plane, there is a right angle between the x and z axes. Now orient the y axis to be perpendicular to them both, and you have our coordinate system. You might wish to imagine a transparent sphere centered on these coordinates, with every star other than the Sun fixed to it. This is the celestial sphere. If you sit on top of this sphere and look down at Earth, you will see it rotating counterclockwise on its z axis.
The beauty of this coordinate system is that (neglecting small perturbations that will be described below) the orbit of any satellite is a fixed ellipse. The satellite moves around the ellipse, but the ellipse itself remains stationary. It takes six numbers to describe such an orbit. The six could be simply position (three numbers) and velocity (three numbers) at some reference time, but a different set is used in practice and is worth getting used to. Two numbers describe the plane and direction of rotation. A satellite's ascending node is the direction from the origin to the satellite when it ascends through the equatorial plane going north. The right ascension (RA) of the ascending node is an angle measured counterclockwise (as viewed from the North Pole) from the x axis to the ascending node, an angle between 0 and 360 degrees. The other number is the angle in degrees between the equatorial plane and the plane of rotation, the orbit's inclination (IN). For prograde (counterclockwise) orbits, 0�IN<90. For retrograde (clockwise) orbits, 90<IN�180. All orbits that go over the North Pole are polar and have IN=90. Orbits with IN=0 or IN=180 are all equatorial, but the first is prograde and the second retrograde. Figure 1 illustrates RA and IN for a circular, prograde orbit. In this Earth-centered coordinate system, the Sun's orbit is nearly circular and prograde, with IN=23.5 and RA=0.
Kepler's Laws
As Johannes Kepler discovered and Isaac Newton first showed in 1685, the solution of the two-body problem is that the path of body A with respect to body B is a conic section. When the conic section is a parabola or hyperbola, body A "escapes" and never returns; otherwise, body A (the satellite) repeatedly travels around an ellipse with one focus at body B (Earth, in the present application). This is Kepler's first law. Three additional numbers are required to determine this ellipse within the plane already determined by RA and IN. Systems for doing this vary (the details are not important for the moment). The sixth and last number locates the satellite on the ellipse at some standard time. After the satellite is located on the ellipse, physics takes over, and the satellite rotates round and round the earth indefinitely.
Kepler's second law states that the time required to go from one orbital position to another is proportional to the area of the circular wedge formed by the line between the earth and the satellite. When the line is long, the satellite moves slowly. Therefore a satellite moves fastest at perigee (closest point to Earth) and slowest at apogee (farthest point).
Kepler's third law states that the period (T) of the orbit is related to its size in that T2 is proportional to r3, where r is the semimajor axis of the ellipse (half its largest diameter). For satellites whose mass is negligible compared to that of Earth, the exact relationship is:
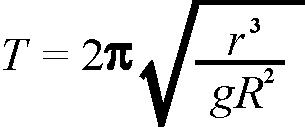
| where | g is the gravitational attraction at Earth's surface (.00981 km/sec2) |
| R is the radius of Earth (6378 km). |
For satellites in circular orbit, r is the radius of the orbit. For example, a satellite in circular orbit 570 km above Earth would have r=6948 km and T=5760 seconds (ninety-six minutes). If atmospheric interactions are ignored, a satellite with r=R would be feasible and would have a period of eighty-four minutes (it would also have a speed of 7.9 km/sec, providing a real thrill to observers as it skims Earth's surface). In practice most satellites stay at least 200 km above the earth to avoid the atmosphere, so think of an hour and a half as a lower bound on any satellite's period. The satellite's mass does not affect the orbit as long as it is small compared to Earth—the formula also works for the Moon, but not for the Sun.
The earth rotates on its axis once every 23 hours and 56 minutes, the length of a sidereal day. Remember that the Sun is moving around the earth in a prograde orbit, and that a (solar) day is the length of time required to have the Sun again overhead at a given point on Earth. After the earth has rotated counterclockwise once, it still needs another 365th of a day (about 4 minutes) to catch up to the Sun. A prograde orbit with a period of one sidereal day (circular or not) is geosynchronous; that is, the satellite's Earth track will be the same every day. Circular, geosynchronous orbits have a radius of about 42,164 km.
A circular, geosynchronous orbit with inclination IN=0 will appear to hover above a point on the equator. These orbits are geostationary. Specifying the fixed point on the equator completely defines the location of a geostationary satellite for all time, so there can be only one geostationary orbit for every longitude. Geostationary orbits are popular for communication satellites because the corresponding ground antennas do not have to move much. Fortunately, since the circumference of the geostationary orbit is 267,000 km, there is room for quite a few satellites. From its position at 5.6 Earth radii above the surface, a single geostationary satellite can see as far as 81 degrees north or south latitude— almost a complete hemisphere. Three or four carefully spaced satellites can cover most of the earth; the missing parts are the polar or ocean regions, where very few people live. This is all very convenient. (On Jupiter, the corresponding orbit would be only 1.25 radii above the surface, and consequently a satellite would not be visible beyond a latitude of 64 degrees. On our sister planet Venus, which hardly rotates, the orbit would be inconveniently far away at a radius of 1.5 million km [244 radii]. In yet another way, the earth turns out to be a good place for the human race.)
Nevertheless, while a satellite can indeed "hover" above a point on the equator and "see" much of the earth's hemisphere below—a feature ideal for receiving and transmitting radio, telephone, and television signals and for viewing major weather formations—the orbital distance of nearly 170,000 miles precludes tactical imaging or electronic intercept locating. These require low Earth orbits.
Effects of Earth's Rotation
Of the six satellite parameters, only RA and IN would be of much use if the earth did not rotate. These two alone would determine the track of the satellite on Earth, with the other four parameters affecting only revisit time and the velocity and altitude of the satellite as it passes over. This would have the advantage of conceptual simplicity—most satellite coverage problems could be investigated with a globe and some means of drawing great circles on it. But the operational disadvantages of a nonrotating Earth would be immense, even putting aside the fact that all life would die out. There would not be any geostationary orbits, for example, since one could not count on the earth to expose itself by rotating under the satellite. In spite of the conceptual complications, Earth's rotation is basically a Good Thing.
The coverage pattern achieved by a satellite on a rotating Earth depends on the relationship between the satellite's period T and Earth's sidereal period E. The ratio Q�E/T is the repetition factor. The orbit is synchronous if Q=1. If Q=2, as in the Global Positioning System, each satellite makes two complete orbits in one sidereal day. A satellite with Q=14/3 would repeat its ground track—the trace of points on the earth's surface directly below the satellite— every 3 sidereal days, after fourteen revolutions. The ground track of a circular satellite with Q=15 and IN=63 is shown in Figure 2. "This satellite appears to weave a kind of "basket" upon the earth in the process of making its fifteen daily orbits, revisiting Norfolk and every other point on its track once a day. Because of the earth's rotation, a single satellite can come reasonably close to every point on Earth once a day, within the latitudes that its orbit is designed to cover. If the mesh of the basket is too coarse, use a second satellite offset by 360/(15x2)=12 degrees of RA. If the revisit time is too large, put multiple satellites in the same orbit.
If Q is an irrational number, then the ground track never repeats! Even when the ground track repeats, some remarkably odd shapes are possible. Figure 3 shows the track of a circular synchronous satellite with IN=45. The track is confined to the predictable latitudes but moves around in a figure-eight pattern. Figure 4 shows the track of an elliptic orbit with Q=2. In Figure 4, apogee occurs twice a day at the two northern cusps; the closeness of the hourly hashmarks means that there the satellite is moving slowly, as is always true in elliptical orbits. There are many Russian Molniya satellites with orbits of this type.
Perturbations
Due to its rotation, Earth is a bit fat around its equator. As a result, the motion of a satellite is perturbed from what it would be if Earth were a perfect sphere. The effect is the same one that applies to a spinning top when Earth's gravity tries to make the axis of spin horizontal. Instead of falling down, the axis of the top's rotation precesses about the vertical. Basically a satellite is just a big top, and the bulge at the equator continually tries to move the satellite's axis of rotation into the equatorial plane. The satellite's reaction is that its axis of rotation precesses about the North Pole—the inclination of the orbit remains constant, but the right ascension (RA) changes slowly with time. RA decreases for prograde orbits and increases for retrograde orbits, with polar orbits unaffected. The magnitude of the RA drift is approximately several degrees per day, depending on the altitude and inclination of the satellite, so the effect on Earth coverage can be substantial over only a few days. Satellite tracking programs invariably account for it.
Orbit precession is an analytic annoyance, but a clever orbit designer can put even this phenomenon to use. Recall that a synchronous orbit passes over the same point on Earth once every sidereal day. If that point is in sunlight at one time, it will be in darkness six months later, because of the Sun's orbit around Earth. This can be awkward if photography is involved; it would be better if the satellite could pass over a given point at the same time(s) every day. Precession can make that happen. If the satellite is in a retrograde orbit, then its axis of rotation will move counterclockwise around the North Pole, just like the Sun. If the axis makes exactly one rotation per year, then the orbit will be Sun-synchronous, the desired effect. Satellites in near-polar retrograde orbits are usually put there with this in mind. They are likely to be in low orbits, since the precession effect dies out quickly with altitude.
Another perturbation that must be allowed for is the inexorable effect of friction, particularly for satellites in low orbit. Sooner or later, every satellite will spiral inward, and if it is not burned up in the atmosphere it will finally crash to Earth. In the meantime, the six parameters of the orbit that approximates the satellite's actual track must be periodically adjusted.
Statistics about Satellites
Satellite databases always include RA, IN, three elliptical parameters, one parameter to locate the satellite on the ellipse, and possibly other information. The three elliptical parameters are:
The sixth parameter locates the satellite on the ellipse at some reference time. The true anomaly is the angle from perigee to the satellite (satellite terminology has inherited terms like "argument" and "anomaly" from the ancient science of astronomy—both are names for angles). The mean anomaly (MA) is the angle from perigee to where the satellite would be if it moved around its orbit at a constant angular rate (which it does not). MA is essentially a measure of time since perigee (it is used in preference to true anomaly in spite of its odd definition).
In theory a single reference time (for example, 1957) would do for all satellites, but in practice each satellite has its own epoch (EP), a time, ideally in the recent past, at which the other six parameters are asserted to have been accurate. Of the six parameters in theory, only MA should depend on EP. In practice the other five also have a slight dependence, because of perturbations.
The most common satellite database format is NASA (or NORAD) format, where each satellite gets three lines. In that format EP is in the second line, along with other data that includes the last two digits of the year of launch (YR). The third line includes IN, RA, EC, AP, MA, and MM, in that order, except that EC is given as an integer that should be multiplied by 10-7. NASA format is invariably called two-line format, apparently with the idea that the first line, which contains only the satellite's name, should not be counted. The six lines below describe TELEDESIC 1 and SPOT 4:
TELEDESIC 1
1 25234U 98012B 98254.15120785 .00007458 00000-0 53265-3 0 1151
2 25234 97.7299 146.7419 0032757 28.1699 332.1290 15.04362321 29606
SPOT 4
1 25260U 98017A 98254.19809564 - .00000044 00000-0 00000-0 0 1496
2 25260 98.7291 327.6528 0000917 87.5494 272.5789 14.20020821 24297
Lines
labelled 1 and 2 have the following format: |
||
|
|
|
01-01 |
Line Number of
Element Data
|
|
Column |
Description of elements in line labelled 2 |
|
01-01 |
Line Number of
Element Data |
|
NASA format does not include a field for the satellite's purpose, owner, or launcher, but such information can be found in other databases. The key field is the satellite number that is shown on both lines in the two-line format. Every satellite has a unique number, and it never changes. The numbering is sequential, so it is correct to conclude that over 25,000 satellites or other pieces of space debris had already been launched when SPOT 4 went up in 1998.
For further information, try T. S. Kelso's web page at http://celestrak.com/. The Federation of American Scientists (http://www.fas.org/) also contains an interesting space policy link.
Alan Washburn is a professor in the Operations Research Department at the Naval Postgraduate School. His publications include papers on search theory (including search from satellites), optimization, probability analysis, and game theory. His military interests are in mine warfare, antisubmarine warfare, munitions planning, and information warfare. A complete listing of Professor Washburn's publications is available on the World Wide Web at http://www.nps.navy.mil/~opnsrsch/roster.html.