Vehicle path-planning in three dimensions using optics analogs for optimizing visibility and energy cost
Neil C. Rowe and David H. Lewis
Department of Computer Science, code CS/Rp, U.S. Naval Postgraduate School, Monterey, CA 93943
Abstract
Path planning is an important issue for space robotics. Finding safe and energy-efficient paths in the presence of obstacles and other constraints can be complex although important. We have been investigating high-level (large-scale) path planning for robotic vehicles in three-dimensional space with obstacles, accounting for (1) energy costs proportional to path length, (2) turn costs where paths change trajectory abruptly, and (3) "safety costs" for the danger associated with traversing a particular path due to visibility or invisibility from a fixed set of observers. We find paths optimal with respect to these cost factors. We have in mind autonomous or semi-autonomous vehicles operating either in a space environment around satellites and space platforms, or aircraft, spacecraft, or smart missiles operating just above lunar and planetary surfaces. One class of applications concerns minimizing detection, as for example determining the best way to make complex modifications to a satellite without being observed by hostile sensors; another example is verifying there are no paths ("holes") through a space defense system. Another class of applications concerns maximizing detection, as finding a good trajectory between mountain ranges of a planet while staying reasonably close to the surface, or finding paths for a flight between two locations that maximize the average number of "landmark" points visible at any time along the path (to minimize the chance of straying from the best path).
This paper is to appear in the Proceedings of the NASA Conference on Space Telerobotics, January 1989, Pasadena CA.
1. Our approach
Our major innovation is to view free space as a set of irregular polyhedra for path-planning purposes. Most previous explorations have divided space into a uniform lattice of cubes, and plan transitions between the centers of cubes. We think this leads to unnecessarily inefficient programs since large portions of space are very homogeneous in traversal characteristics while other portions are very inhomogeneous, so a uniform-resolution representation can be wasteful. And by grouping space into irregular meaningful regions (like space visible from a particular set of observers), the problem becomes more intuitive to a human; debugging is simplified, and human heuristics are easier to obtain. To further simplify matters, we assume energy expenditure is a proportional to path length, and that visibility danger is binary (either yes or no) so it only changes abruptly and at the boundary of what we call "visibility regions". We have already investigated a similar problem in two dimensions, that of finding routes across overland terrain with forests, shrub, grasslands, and other terrain types of varying traversability, using the idea of formulating "weighted" regions, regions of homogeneous characteristics [5, 4, 3, 6]. Apparently the only similar attempts such as [7] to find paths through irregular regions in three dimensions have been limited to obstacle-avoidance criteria, and much of that work is highly theoretical.
Since our goal is to find paths good with respect to energy, turn, and visibility cost, a path optimal with respect to those criteria is desirable if obtainable without excessive effort. The calculus of variations is the general solution to optimal-path problems; its methods are complex and few of its problems can be solved in a closed form. Fortunately, the problem we have described does not require it since our optimal paths must be piecewise-linear, where the pieces correspond to visibility regions. This follows from an important general principle we have used in many areas of path planning, the "shortcut meta-heuristic": optimal paths only turn or curve when any shortcut across the turn would be worse. No such conditions are present, in the problem described above, in interiors of regions of homogeneous visibility and homogeneous cost per unit traversal.
Furthermore, we can show that the piecewise-linear optimal paths in our problem must obey Snell's Law from optics when they do turn on the boundaries of regions, if we make a few reasonable assumptions. We assume that path energy cost is proportional to the length of the path, as for example with uniform-thrust and uniform-speed aircraft. We assume that visibility danger or benefit from a single observer is a utility, positive or negative, also proportional to path length, as with a uniform-speed vehicle that has a uniform probability of being noticed anytime when visible. A positive utility means it is desirable to be seen, a negative utility the opposite. Any path-optimization problem in which cost is proportional to path length within homogeneous regions of space is equivalent to the optics problem of tracing light rays through optical media of locally-homogeneous indices of refraction, as for example a lens system. It follows that Snell's Law applies on the region boundaries in our problem.
The main challenge for our path planning becomes the geometric construction
of visibility regions. We assume a fixed set of point observers. We model all
obstacle (impermissible-traversal) regions as polyhedra as in [8], methods of
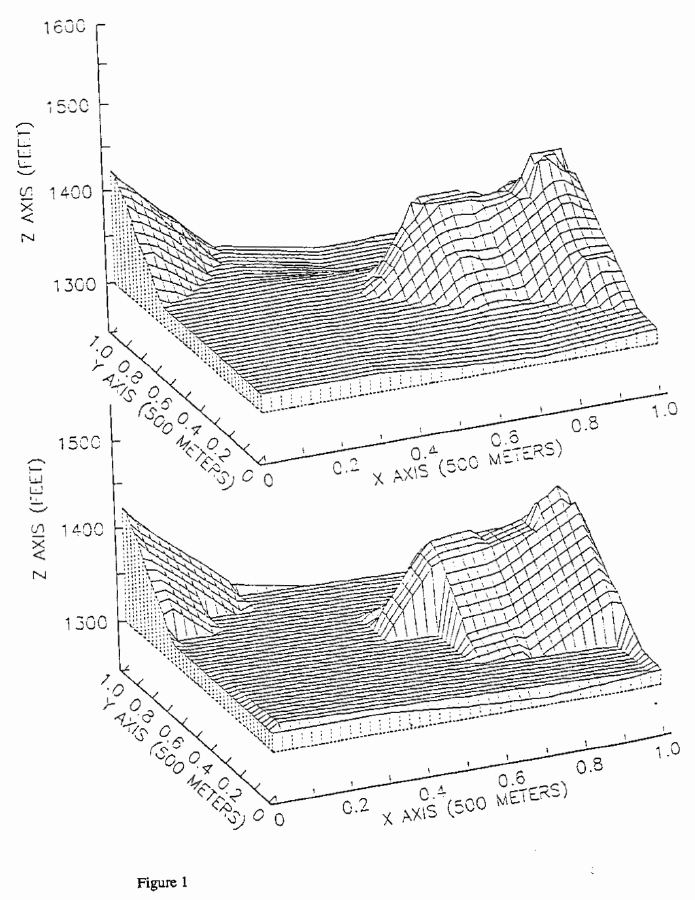
which are illustrated in Figure 1, which shows example terrain near Jolon,
California (top picture), and one polyhedral fit to it (bottom picture). (To
ensure paths stay at least K units from obstacles, we can further offset the
polyhedral facets by K.) We also model visibility regions as polyhedra
representing regions of space within which all the same things can be seen;
they are polyhedra because each point observer and each convex edge of an
obstacle determine a plane wherein two facets of two adjacent visibility
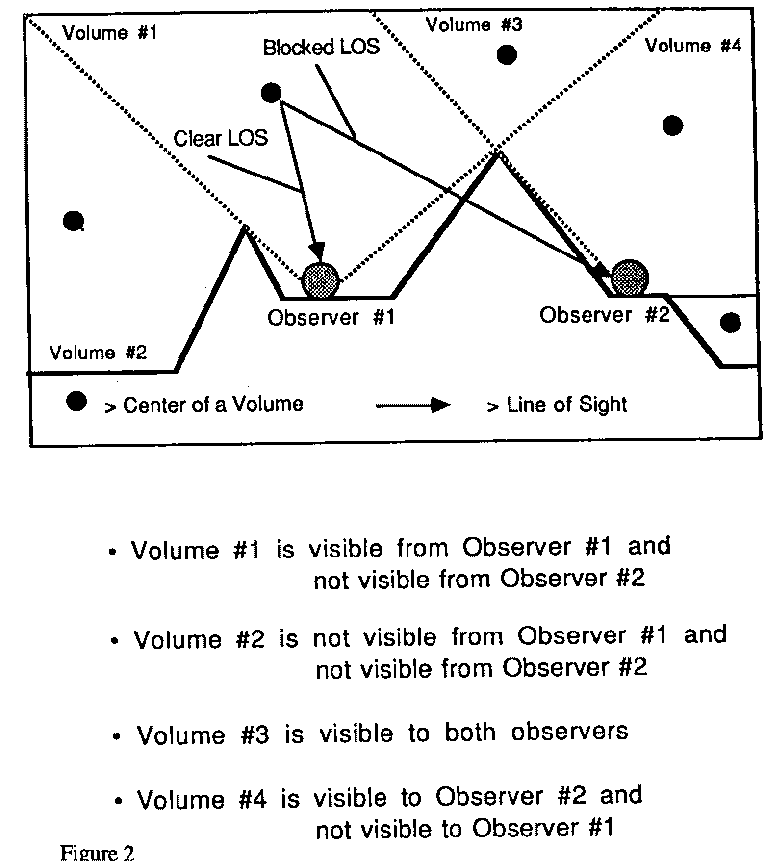
regions must lie. Figure 2 illustrates the visibility-region construction in
cross section. Each region can be assigned a uniform probability of detection
per unit traversal distance within it; if more than one observer can see a
region, we assume observational independence and the total probability of
detection is the inverse of the product of inverses of the separate
probabilities of detection. This approach leads to recursive resubdivision of
regions, and can be managed by an object-oriented system storing information
about regions, facets, edges, and vertices.
This approach is surprisingly general. Work done against gravity can be ignored, since we are assuming a fixed start and goal, and the work between them must be independent of the path. Work against atmospheric resistance to the object traversing the path can also be ignored whenever the resistance is linearly proportional to the velocity. (The traversal speed then need not be constant, since the total work done against air resistance depends only on the path length). The only remaining major factor is turn cost. Since we are doing high-level path planning, we can assume the object traversing the path is negligible in size with respect to the geometry of the path, and we can assume turns are abrupt, not gradual. Then turns at a particular velocity require a momentum-vector change proportional to the sine of half the angle of the heading change. In an atmosphere, a well-designed craft requires minimal energy expenditure to make this momentum change, but in space or thin atmospheres, all this must be done by thrust. Then by using Lagrange multipliers it is straightforward to show the following generalization of Snell's Law must hold for the turn on the boundaries of regions:
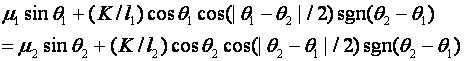
where the μ terms are the cost per unit distance in the two regions per friction and visibility factors, the θ terms are the entering and leaving path angles with respect to the normal to the boundary between the two regions, K is the constant of proportionality between traversal cost and turn cost, and the l terms are the lengths of the path within each of the two regions (recall the path must be linear within these regions). When K=0 this becomes Snell's Law. This equation is almost equally straightforward to apply in "ray tracing" of optimal paths as Snell's Law.
2. Search methods
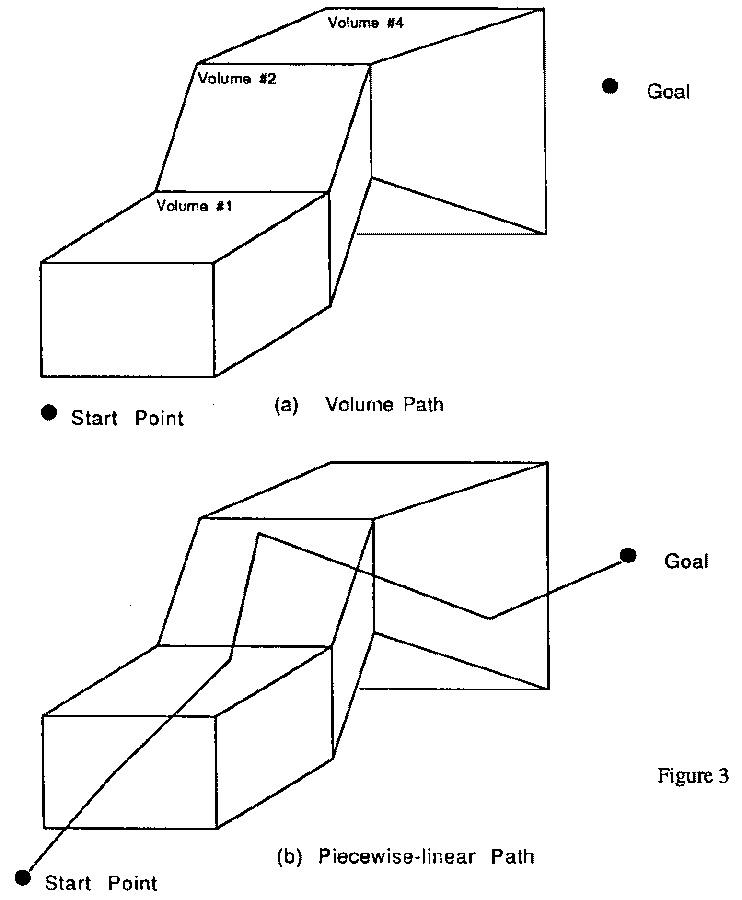
Given a start point, a goal point, and a set of polyhedral regions of space
homogeneous in traversal characteristics, search for an optimal path breaks
naturally into two parts (see Figure 3): finding a good sequence of adjacent
volumes through which the path can go, and optimizing the path through those
volumes by iterative adjustment. The first step can be done by an A* search
using the centers of the regions as nodes, an idea used before for
nonoptimal-path finding [1, 2], but which we enhance by requiring Snell's-Law
turns on region boundaries. The length of path segment within each volume
determines its contribution to the cost of the path. A* search can provide the
K best volume sequences, or all sequences with cost within C of the best cost.
By a straightforward extension of the two-dimensional case considered in [3, 4,
and 5], the optimal path must lie within an ellipsoid whose foci are the start
and goal, whose major axis is the distance D between start and goal times the
ratio R of the cost of the highest-cost region to the lowest-cost region, and
whose minor axes are ![]() .
.
For a sequence of volumes, we must then find the best path through it. Such an optimal path must be piecewise-linear, turning only on region boundaries, and turning only in accordance with Snell's Law except when the boundary is an obstacle (when it must be a obstacle edge, which follows from the shortcut meta-heuristic). This is a convex optimization problem if we ignore turn cost, as is provable from Snell's Law. Thus almost any iterative optimization technique can be used without fear of converging to the wrong local optimum. (Even with turn cost included, we can use the same techniques heuristically.) The optimization variables represent points on the facets of polyhedra, points with only one degree of freedom each because there are only two cases for path turns: (1) points on obstacle edges, where the turn must enclose the obstacle; and (2) points on non-obstacle-region facets, where Snell's Law must hold for the turn, and thus where all the successive such path segments must be coplanar between obstacle encounters. We can thus partition a path into alternating episodes of successive Snell's-Law turns and successive obstacle-following turns, and each episode can be optimized separately with each variable varying along one dimension. The iteration need not be run to convergence for every volume sequence under consideration, since we may be able to see after a while that the result could not better that of best volume sequence found so far. Lower bounds on costs help for this; they can be obtained by considering the minimum distance between two facets of a polyhedron.
3. Implementation
To explore these ideas we did a partial implementation in Common Lisp with
Flavors on a Texas Instruments Explorer II. To simplify path planning, we
created more polyhedral visibility regions than strictly necessary (for
instance, we subdivided all regions until they were convex, to avoid checking
that paths between two facets of a region stay within the region). In the
second (optimization) phase, we only examined the best region sequence found by
the first search. And to simplify the optimization itself, we did not include
turn costs (though we did in the first phase or A* search). Figure 4 is the
block diagram of our implementation.
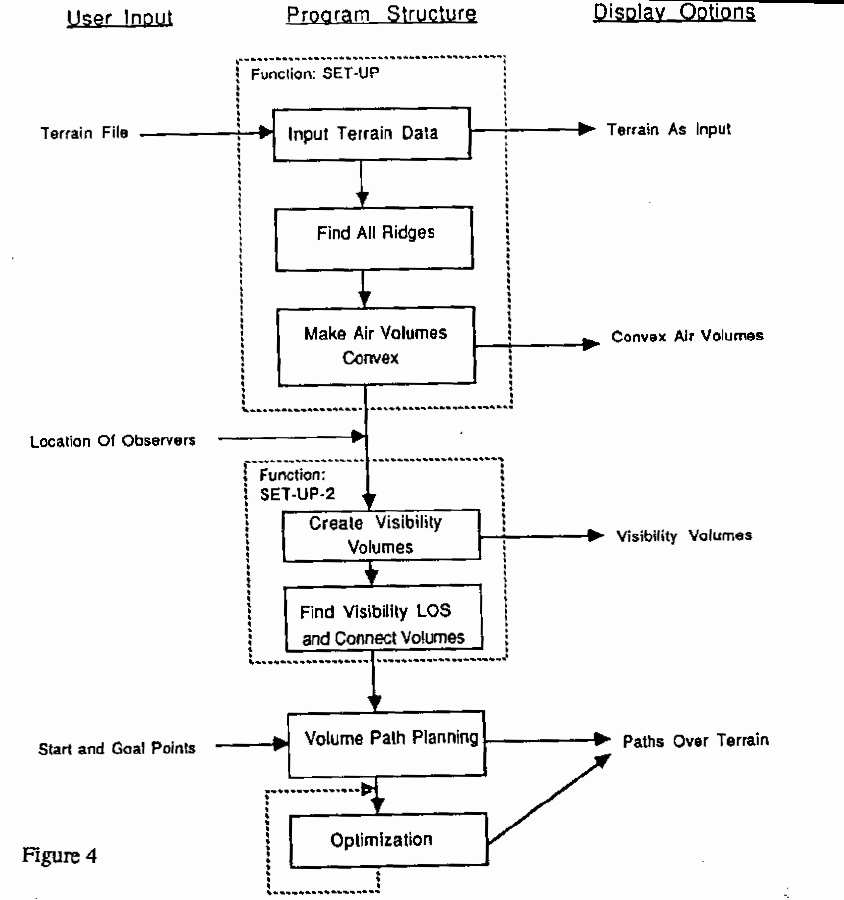
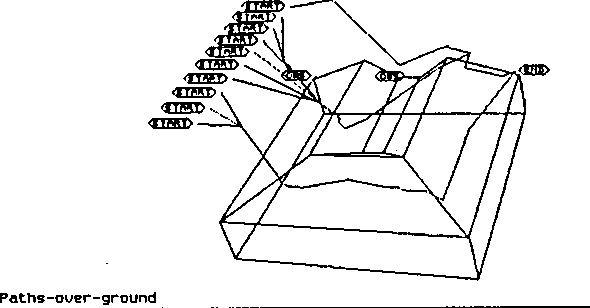
Figure 5 shows solutions to some simple problems given our program. A single
observer is stationed in a "box canyon" in the middle of the far side
of the terrain, and visibility by this observer is taken as undesirable; the
goal point is outside the canyon to the right in the back; and a variety of
start points are chosen along the left side of the picture outside the box
canyon. While we did not continue the optimization long enough to completely
smooth out the paths, note that optimal paths starting toward the front stay
hidden from the observer, but paths starting toward the back find it better to
be seen by the observer for a short time rather than make a long and
costly-energy detour.
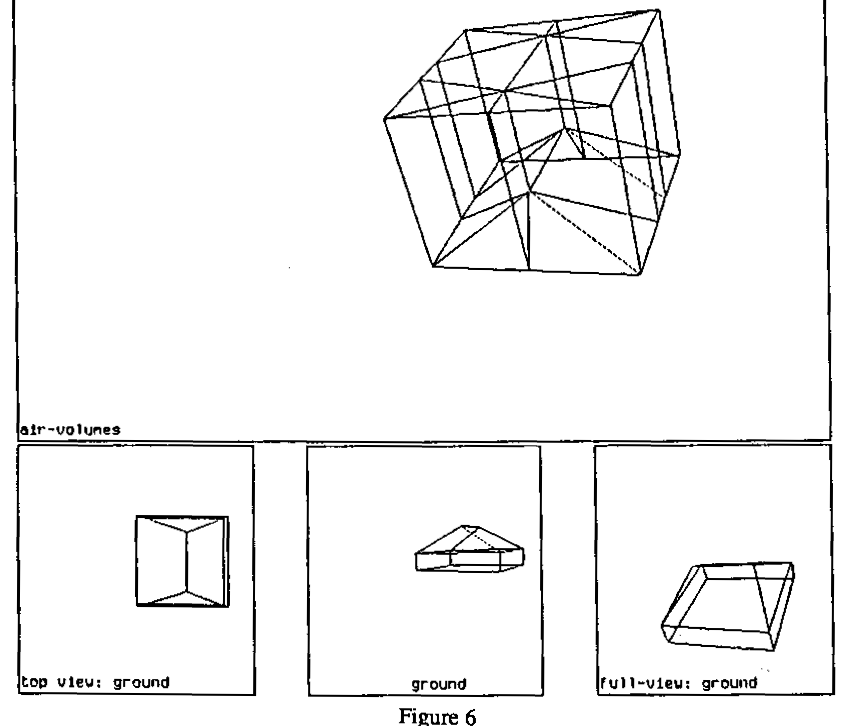
To see a little of what the program does to get such results, Figure 6 shows
the convex air regions created, preliminary to visibility analysis, for an
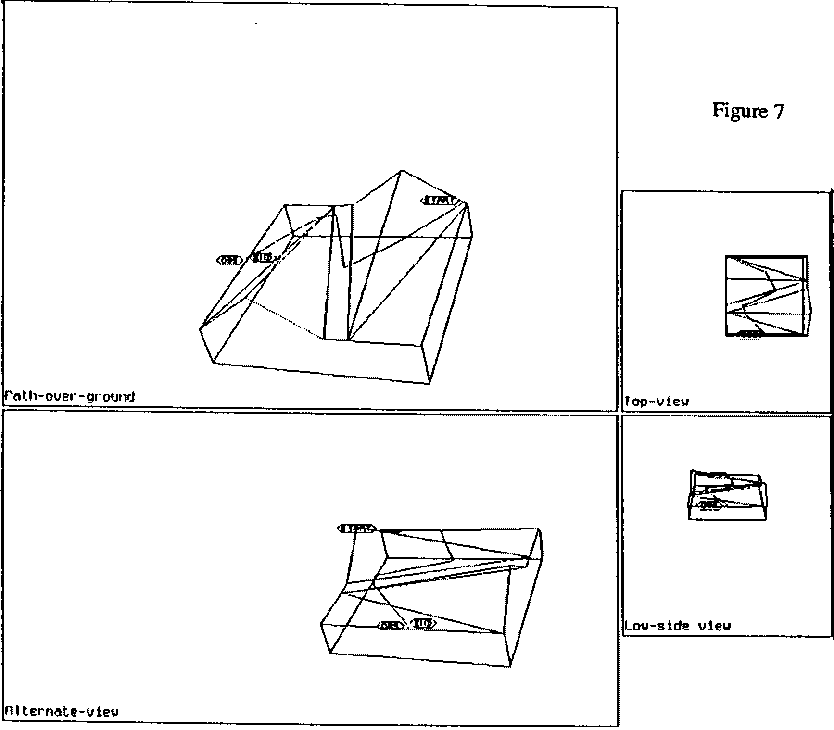
obstacle polyhedron representing a hill or ridge. To illustrate the search
phases, Figure 7 shows terrain with two ridges, start and goal points near the
ground on the far right and the far left sides of the two ridges, and the
result of fitting a piecewise-linear path through the centers of the facets
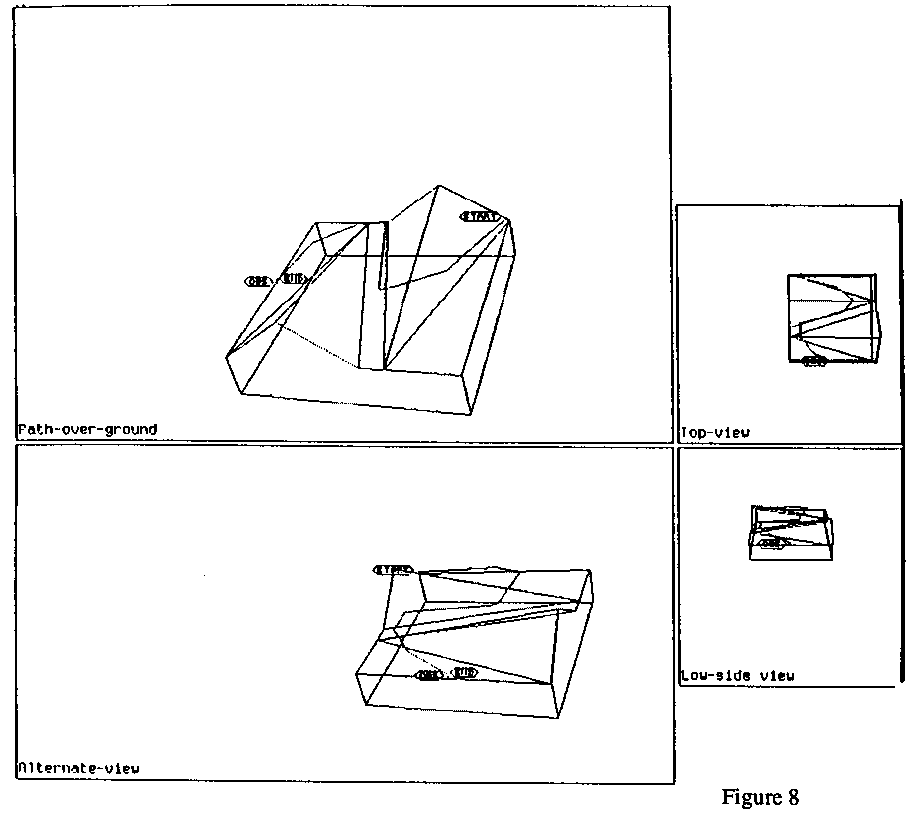
found in sequence by the region-sequence (A*) search; Figure 8 is the result
after optimization. While the difference was not dramatic, we did average a ten
percent improvement in path cost by optimizations in our experiments.
Most of the computation time by far for our implementation was in the computation of the visibility regions. But this could be easily improved significantly by better algorithms; for instance, we use only a very simple method to intersect planes and polyhedra. However, region-computation time may often not be important because regions usually need only be computed once, like the surface of the planet or the surface of a space object; once computed, they can be used repeatedly for all path planning on that same terrain.
4. Conclusions
The work so far is just a first step in what we hope will be a continuing research effort. We have yet to integrate well our terrain planar-patch modeling into the path planning. Clearly we need a more comprehensive path-cost calculation, incorporating atmospheric air resistance, a less-absolute notion of visibility, wind effects, and temperature-variation and other weather effects. Some kinds of aircraft and spacecraft show significant nonlinearity in the tradeoff between power expenditure and thrust, and this needs to be modeled. We intend to explore simple nonhomogeneous regions, for which optimal paths can be curves. Currently we are having problems with numerical errors in long-and-narrow regions, whose centers are misleading, so fixing that problem is a high priority. But the methods we are exploring are more intuitive than current methods, as well as being more efficient for many problems because of the fewer regions of space that need to be created. They clearly deserve further investigating.
5. Bibliography
[1] R. Chavez and A. Meystel, "Structure of intelligence for an autonomous vehicle", IEEE International Conference on Robotics, Atlanta, Georgia, 1984, 584-591.
[2] K. Rueb and A. Wong, "Structuring Free Space as a Hypergraph for Roving Robot Path Planning and Navigation", IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-9, 2, March 1987, 263-273.
[3] R. Richbourg, "Solving a class of spatial reasoning problems: minimal-cost path planning in the Cartesian plane", Ph.D. thesis, U. S. Naval Postgraduate School, June 1987, published as technical reports NPS52-87-021 and NPS52-87-022.
[4] R. F. Richbourg, N. Rowe, N. Zyda, and R. McGhee, "Solving global, two-dimensional routing problems using Snell's Law and A* search", Proceedings of the IEEE International Conference on Robotics and Automation, Raleigh, North Carolina, February 1987, 1631-1636.
[5] N. Rowe, "Roads, rivers, and rocks: optimal two-dimensional route planning around linear features for a mobile agent", accepted to International Journal of Robotics Research, July 1988.
[6] N. Rowe and R. Ross, "Optimal grid-free path planning across arbitrarily-contoured terrain with anisotropic friction and gravity effects", technical report NPS52-89-003, Department of Computer Science, Naval Postgraduate School, Monterey, California, November 1988.
[7] M. Sharir and A. Schorr, "On shortest paths in polyhedral spaces", SIAM Journal on Computing, 15, 1 (February 1986), 193-215.
[8] S. H. Yee, "Three algorithms for planar-patch terrain modeling", M. S. thesis, U. S. Naval Postgraduate School, June 1988.
Acknowledgement: This work was prepared in conjunction with research conducted for the Naval Air Systems Command and funded by the Naval Postgraduate School.