Image processing includes a diverse set of methods for manipulation of digital images [1, 4, 5]. These include modification and enhancement (as by increasing the contrast or changing the image shape) and analysis (as by counting desired objects within the image). Digital images can be thought of as two-dimensional arrays whose entries or "pixels" represent degrees of brightness (or red, green, and blue brightnesses if a color image) at evenly spaced locations. Image processing is distinguished from computer graphics in its predominant emphasis on images originally produced by cameras and in a goal of analysis rather than synthesis of images.

Many image-processing methods are suggested by analogies to visual processing in brains. The apparent ease with which we see is deceptive since much occurs of which we are not conscious. Much of the back of the human brain and key centers behind the eyes are devoted to vision, as is proved when injuries damage them. While we do not yet have detailed understanding of natural visual processing, it appears to be highly distributed. Much of this distributed processing handles different locations in the image, with some of it handling different visual properties at the same location.

Image processing methods group into several categories. One category manipulates image formats and converts between them [3]. There is no single standard data format for digital images since a variety of uses must be addressed. Bitmaps like those provided with BMP, RGB, XBM, and XWD formats are two-dimensional arrays that are well suited for processing of small clusters of adjacent pixels ("local neighborhoods"). But since bitmaps require considerable space, most formats are compressed; the most popular currently are the JPEG, GIF, and TIFF formats. GIF format limits the picture to a small number of colors, and approximates other colors by mixing pixels from its palette ("dithering"). JPEG format averages properties over subregions of the image and approximates the deviations around those averages; it also does "run-length encoding" that replaces repeated patterns with a description of the pattern and its number of repetitions. Such compressed formats aim to preserve most (but not all) the information in a digital image. Routines are needed to convert to and from different formats. Video formats include the television standards NTSC, PAL, and SECAM, and the video compression standard MPEG (see below).

Other image processing enhances appearance or viewability. Important examples are:

1. Averaging brightness or color values within local neighborhoods across the image to "smooth" or blur it;
2. Functions applied to the brightness or color of pixels, like for instance reddening a too-blue image, evening the range of brightness in an image ("histogram equalization"), and adjusting for nonlinearities in camera?s response to changing brightness; and
3. Mapping of pixel locations to new places, as when an image size, shape, or orientation is changed.

Figure 1 shows an example aerial photograph, and Figure 2 shows the result of blurring and widening the contrast between dark and light to reduce minor details. Such local-neighborhood processing is a kind of "digital filtering".

Figure 1: Example aerial photograph.

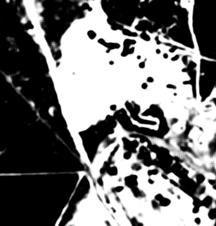Figure 2: Blurring and contrast enhancement of Figure 1.

Another category of processing finds shapes and objects in images ("segmentation"). Human and animal visual processing is especially good at this because it is essential for dealing with the world. Methods can find a desired shape like a face in an image by correlation ("recognition"). A more general approach is to find "edges" along which the brightness or color change exceeds some threshold; a variety of "edge operators" like the Sobel, Laplacian, and Canny do this. This results in a set of pixels denoting edges of objects, but the pixels may not form unbroken boundaries. Figure 3 shows an edge image for Figure 1 from the Canny operator. Another general approach is to find "regions" of contiguous pixels that represent objects. A simple way is to find all pixels greater than a threshold brightness, but this only is helpful when desired objects are consistently brighter or darker than a background. A more general way is to find contiguous regions of consistent brightness or color. Assigning pixels to such regions can be done in a single row-by-row pass through the image, but enumerating all the pixels within a region requires additional effort. Such regions can be incorrectly connected if a small part of their boundary connects, so they may need to be split too in a "split-merge" algorithm. However, areas without a consistent boundary may still be distinguished by a difference in "texture" or local-neighborhood statistics, like the standard deviation of the brightness which can distinguish smooth manmade surfaces from irregular natural ones. A wide variety of texture metrics have been explored, and textures can be recognized by neural networks (see Neural Networks).

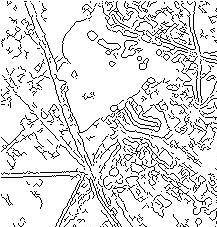
Figure 3: Edge image computed from Figure 1.

Some image processing maps image data to an equivalent transform space in which certain processing is easier. The most common transforms are:

1. The Fourier transform in two dimensions maps the image to "spatial frequencies", and it is useful for finding regular patterns in an image and for removing blur.
2. Wavelet transforms are a generalization of the Fourier transform that also codes locations of regularities in the image; there are varieties based on the wavelet functions used.
3. The basic Hough transform maps edge points to possible lines on which the points could lie, and is used to find evidence for broken straight lines in an image. Variants on the Hough transform can find shapes like circles and rectangles, but are more difficult to compute.

Figure 4 shows the result of using the Hough transform of Figure 3 to rule out edge pixels (like those on curved boundaries) not part of major linear features of the image, thereby simplifying the edge image. All these transform results can be searched for patterns. Or the result may be filtered to simplify it and mapped back to an image by the inverse transform, a popular use of the wavelet transform.

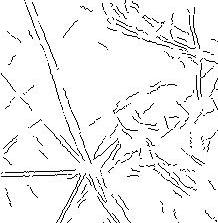
Figure 4: Improvement of Figure 3 using the Hough transform.

Segmentation and pattern finding results in a "binary image" in which each pixel is either "on" or "off". Special processing methods apply to binary images. Metrics can be applied to edges or regions to characterize their shapes for object identification and classification. Example metrics for individual regions are the ratio of the width to the length (which measures elongation) and the ratio of the area to the square of the perimeter (which measures circularity). Example metrics for region sets are their number, their density per million pixels, and their average edge orientation. A binary image can be matched to its generating image to obtain metrics like the average color or texture of a region. Metrics like these permit clustering and nearest-neighbor calculations to recognize larger-scale patterns in an image. Additional methods applied to binary images include logical operations on corresponding pixels of two images (like an exclusive-or operation to find pixel differences), erosion and dilation (to thin or thicken features), and "masking" or selection of pixels in one image (useful for collages of multiple images).

Additional techniques can reason about the three-dimensional world when images are two-dimensional [5]:

1. Some images produced by radiating devices like radar and sonar give distance directly to an object by time-of-flight measurement; edges of objects can be inferred at discontinuities in distance.
2. Tomographic images represent densities encountered by rays through an object, and can be used to reconstruct three-dimensional shapes by solving equations. Tomography using X-rays, magnetic resonance, or sound waves has many important applications in medicine and industry.
3. Matched stereo pairs of images (images of the same scene taken by two cameras a short distance apart) can be used to infer three-dimensional shape by iterative match-optimization ("relaxation") methods that match their pixels.
4. Even a single image can provide three-dimensional clues from shadows and the relative brightness of surfaces (since most surfaces are brighter the more directly they face illumination) which a different kind of iterative relaxation can use to determine the shape.

Some images occur in sequences like those of video. Processing methods can exploit the usually large similarities of successive images. This is done in the MPEG video standard, which compresses redundancy both between successive images and within each image. Moving and rotating objects can be automatically tracked through successive images by techniques that match pixels or edges between images; as with stereo matching, the goal is to find, if possible, locally consistent mappings where neighbors map to neighbors. If sufficiently similar, images can just be subtracted to create a "difference image" representing the inconsistencies, and these have many applications in aerial photography and medicine. But this requires the images coincide or be "registered", which requires work if the camera or subject is not stationary.

A variety of additional special processing produces artificial images and computer graphics, including interpolation, warping, and morphing.

Most image processing methods are computation intensive and linearly decomposable (see Linearizability and Sequential Consistency) and thus well suited to parallel or distributed implementation. This is because most apply functions independently to individual pixels or to local neighborhoods of the image. Even when neighborhoods overlap as in blurring operations, read conflicts can be avoided by copying the data, while write conflicts are generally avoided since each result can be stored in a different location (see Parallel Algorithms and Parallel Processing). Exceptions, however, are the transforms, which entail sums over many data items and could incur frequent write conflicts. So parallel algorithms are a natural way to think about image processing, and most image-processing toolkit software emphasizes neighborhood operations that are consistent with this viewpoint. And human visual processing is highly parallel.

Currently the potential of parallel and distributed image processing has been little realized. Real-time applications (see Real-Time Systems) like robotics and military-image analysis have explored distribution of image subtasks to processors [2]. But fast specialized architectures for image processing have not often appeared cost-effective against the slower standard architectures, like the PC personal computer and current network technology, that are subject to intense competitive pressures toward improvement in speed and price. Eventually, however, the pace of improvement must slow (perhaps as lower limits on device size are reached) and a niche market will appear. Certainly large speedups are possible: Parallel neighborhood processing on a 1000 by 1000 pixel image, a little better than a standard television picture, could run nearly one million times faster. Eventually distributed image-processing packages will be standard with image-processing software, and perhaps parallel image processors will come bundled with computer systems much in the way that microphones and video cameras are increasingly bundled today.

[1] Rafael C. Gonzalez and Richard E. Woods, Digital Image Processing, third edition, Reading, MA: Addison-Wesley, 1992.

[2] Phillip A. Laplante and Alexander D. Stoyenko (eds.), Real-Time Imaging: Theory, Techniques and Applications, New York: IEEE Press, 1996.

[3] John Miano, Compressed Image File Formats: JPEG, PNG, GIF, XBM, BMP, Reading, MA: Addison-Wesley / ACM Press, 1999.

[4] James R. Parker, Algorithms for Image Processing and Computer Vision, New York: Wiley, 1996.

[5] John C. Russ, The Image Processing Handbook, 2nd edition, Boca Raton, FL: CRC Press, 1995.

Data Mining see Image Processing.

Linearizability and Sequential Consistency see Image Processing.

Multimedia Systems see Image Processing.

Multimedia Information Systems see Image Processing.

Neural Networks see Image Processing.

Parallel Algorithms see Image Processing.

Parallel Processing see Image Processing.

Robotics see Image Processing.

World Wide Web see Image Processing.

Color map: An integer encoding of colors that represents indexes into a table giving red, green, and blue parameters for that color. Colors not represented in the table must be mapped to the closest entry.

Image processing: Processing software applied to digital images.

JPEG: "Joint Photographers Expert Group", a compressed digital-image format defined from an international standard. Its compression loses some information but usually not much.

GIF: "Graphics Interchange Format", a popular compressed digital-image format that uses a color map.

MPEG: "Moving Pictures Experts Group", a compressed digital-video format defined from an international standard.

Pixel: The fundamental element of an image, representing the brightness or color at a particular location. Pixels are usually represented as a single 8-bit integer (for black-and-white or color-mapped color images) or three such integers (for other color images).

Segmentation: In image processing, the separation of an image into regions of locally homogeneous characteristics.